|
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units or the US customary system. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitude (mathematics), magnitude and Direction (geometry, geography), direction of a force are both important, force is a Euclidean vector, vector quantity. The SI unit of force is the newton (unit), newton (N), and force is often represented by the symbol . Force plays an important role in classical mechanics. The concept of force is central to all three of Newton's laws of motion. Types of forces often encountered in classical mechanics include Elasticity (physics), elastic, frictional, Normal force, contact or "normal" forces, and gravity, gravitational. The rotational version of force is torque, which produces angular acceleration, changes in the rotational speed of an object. In an extended body, each part applies forces on the adjacent pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-dimensional Euclidean space. In geometry, one often assumes uniform mass density, in which case the '' barycenter'' or ''center of mass'' coincides with the centroid. Informally, it can be understood as the point at which a cutout of the shape (with uniformly distributed mass) could be perfectly balanced on the tip of a pin. In physics, if variations in gravity are considered, then a '' center of gravity'' can be defined as the weighted mean of all points weighted by their specific weight. In geography, the centroid of a radial projection of a region of the Earth's surface to sea level is the region's geographical center. History The term "centroid" was coined in 1814. It is used as a substitute for the older terms "center of grav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
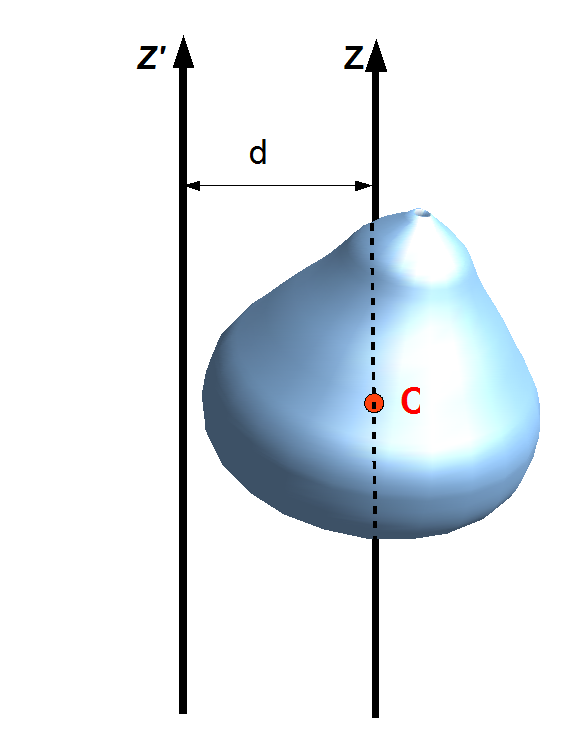
Parallel Axis Theorem
The parallel axis theorem, also known as Huygens–Steiner theorem, or just as Steiner's theorem, named after Christiaan Huygens and Jakob Steiner, can be used to determine the moment of inertia or the second moment of area of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's center of gravity and the perpendicular distance between the axes. Mass moment of inertia Suppose a body of mass is rotated about an axis passing through the body's center of mass. The body has a moment of inertia with respect to this axis. The parallel axis theorem states that if the body is made to rotate instead about a new axis , which is parallel to the first axis and displaced from it by a distance , then the moment of inertia with respect to the new axis is related to by : I = I_\mathrm + md^2. Explicitly, is the perpendicular distance between the axes and . The parallel axis theorem can be applied with the stretch rule and perp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Of Area Of An Arbitrary Shape
Moment or Moments may refer to: Science * Moment (mathematics), a concept in probability theory and statistics * Moment (physics), a combination of a physical quantity and a distance ** Moment of force or torque Time * Present time * An instant * Moment (unit), a medieval unit of time Technology * Moment space surveillance complex, a Russian military apparatus * Samsung M900 Moment, an Android phone Arts Film and television * ''Moment'' (film), a 1978 Yugoslav film * ''Moments'' (1974 film), a British drama starring Angharad Rees * ''Moments'' (1979 film), a French-Israeli film * ''Moments'' (talk show), a Philippine TV celebrity talk show Music and dance * Moment form, a musical concept developed by Karlheinz Stockhausen * ''Moment Rustica'' (ballet), a Martha Graham ballet * '' Momente'' or ''Moments'', a musical composition by Stockhausen * The Moments, American R&B vocal group Albums * A Moment, a 1994 album by Lalah Hathaway * ''Moment'' (Dark Tranquillity a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Moments Of Inertia
The moment of inertia, denoted by , measures the extent to which an object resists rotational acceleration about a particular axis; it is the rotational analogue to mass (which determines an object's resistance to ''linear'' acceleration). The moments of inertia of a mass have units of dimension ML2 (ass× engthsup>2). It should not be confused with the second moment of area, which has units of dimension L4 ( engthsup>4) and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia or sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases, the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. In calculati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Of Inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relatively to a rotational axis. It is the ratio between the torque applied and the resulting angular acceleration about that axis. It plays the same role in rotational motion as mass does in linear motion. A body's moment of inertia about a particular axis depends both on the mass and its distribution relative to the axis, increasing with mass and distance from the axis. It is an intensive and extensive properties, extensive (additive) property: for a point particle, point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second Moment (physics), mome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |