|
Search Games
A search game is a two-person zero-sum game which takes place in a set called the search space. The searcher can choose any continuous trajectory subject to a maximal velocity constraint. It is always assumed that neither the searcher nor the hider has any knowledge about the movement of the other player until their distance apart is less than or equal to the discovery radius and at this very moment capture occurs. The game is zero sum with the payoff being the time spent in searching. As mathematical models, search games can be applied to areas such as hide-and-seek games that children play or representations of some tactical military situations. The area of search games was introduced in the last chapter of Rufus Isaacs' classic book "Differential Games" and has been developed further by Shmuel GalS. Gal, ''Search Games'', Academic Press, New York (1980)S. Alpern and S. Gal, The Theory of Search Games and Rendezvous', Springer (2003). and Steve Alpern. The princess and monster ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero-sum Game
Zero-sum game is a Mathematical model, mathematical representation in game theory and economic theory of a situation that involves two competition, competing entities, where the result is an advantage for one side and an equivalent loss for the other. In other words, player one's gain is equivalent to player two's loss, with the result that the net improvement in benefit of the game is zero. If the total gains of the participants are added up, and the total losses are subtracted, they will sum to zero. Thus, Fair cake-cutting, cutting a cake, where taking a more significant piece reduces the amount of cake available for others as much as it increases the amount available for that taker, is a zero-sum game if marginal utility, all participants value each unit of cake equally. Other examples of zero-sum games in daily life include games like poker, chess, sport and Contract bridge, bridge where one person gains and another person loses, which results in a zero-net benefit for every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rufus Isaacs (game Theorist)
Rufus Philip Isaacs (June 11, 1914 – January 18, 1981) was an American game theorist especially prominent in the 1950s and 1960s with his work on differential games. Biography Isaacs was born on June 11, 1914, in New York City. He worked for the RAND Corporation from 1948 until winter 1954/1955. His investigation stemmed from classic pursuit–evasion type zero-sum dynamic two-player games such as the Princess and monster game. In 1942, he married Rose Bicov, and they had two daughters. His work in pure mathematics included working with monodiffric functions, fractional-order mappings, graph theory, analytic functions, and number theory. In graph theory he constructed the first two infinite families of snarks. In applied mathematics, he worked with aerodynamics, elasticity, optimization, and differential games, which he is most known for. He received his bachelor's degree from MIT in 1936, and received his MA and PhD from Columbia University in 1942 and 1943 respectiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shmuel Gal
Shmuel Gal (; born 1940) is a mathematician and professor of statistics at the University of Haifa in Israel. He devised the Gal's accurate tables method for the computer evaluation of elementary functions. With Zvi Yehudai he developed in 1993 a new algorithm for sorting which is used by IBM. Gal has solved the Princess and monster game and made several significant contributions to the area of search games. He has been working on rendezvous problems with his collaborative colleagues Steve Alpern, Vic Baston, and John Howard.S. Gal and J. Howard (2005). Rendezvous-evasion search in two boxes, OPERATIONS RESEARCH. Gal received a Ph.D. in mathematics from the Hebrew University of Jerusalem The Hebrew University of Jerusalem (HUJI; ) is an Israeli public university, public research university based in Jerusalem. Co-founded by Albert Einstein and Chaim Weizmann in July 1918, the public university officially opened on 1 April 1925. .... His thesis advisor was Aryeh Dvoretz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steve Alpern
Steve Alpern is a professor of Operational Research at the University of Warwick, where he recently moved after working for many years at the London School of Economics. His early work was mainly in the area of dynamical systems and ergodic theory, but his more recent research has been concentrated in the fields of search games and rendezvous. He informally introduced the rendezvous problem as early as 1976.Steve Alpern (1976). ''Hide and Seek Games''. Seminar, Institut fur Hohere Studien, Wien, 26 July His collaborators include Shmuel Gal, Vic Baston and Robbert Fokkink. External links Author profilein the database zbMATH zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastru ... References Academics of the University of Warwick American game theorists Living people Courant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Princess And Monster Game
A princess and monster game is a pursuit–evasion game played by two players in a region. Formal definition In his book ''Differential Games'' (1965), Rufus Isaacs defined the game as: This game remained a well-known open problem until it was solved by Shmuel Gal in the late 1970s. His optimal strategy for the princess is to move to a random location in the room and stay still for a time interval which is neither too short nor too long, before going to another (independent) random location and repeating the procedure. The proposed optimal search strategy for the monster is based on subdividing the room into many narrow rectangles, picking a rectangle at random and searching it in some specific way, after some time picking another rectangle randomly and independently, and so on. Princess and monster games can be played on a pre-selected graph. It can be demonstrated that for any finite graph an optimal mixed search strategy exists that results in a finite payoff. This game ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chinese Postman
In graph theory and combinatorial optimization, Guan's route problem, the Chinese postman problem, postman tour or route inspection problem is to find a shortest closed path or circuit that visits every edge of an (connected) undirected graph at least once. When the graph has an Eulerian circuit (a closed walk that covers every edge once), that circuit is an optimal solution. Otherwise, the optimization problem is to find the smallest number of graph edges to duplicate (or the subset of edges with the minimum possible total weight) so that the resulting multigraph does have an Eulerian circuit. It can be solved in polynomial time, unlike the Travelling Salesman Problem which is NP-hard. It is different from the Travelling Salesman Problem in that the travelling salesman cannot repeat visited nodes and does not have to visit every edge. The problem was originally studied by the Chinese mathematician Meigu Guan in 1960, whose Chinese paper was translated into English in 1962. The o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eulerian Path
In graph theory, an Eulerian trail (or Eulerian path) is a trail (graph theory), trail in a finite graph (discrete mathematics), graph that visits every edge (graph theory), edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex (graph theory), vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this: :Given the graph in the image, is it possible to construct a path (graph theory), path (or a cycle (graph theory), cycle; i.e., a path starting and ending on the same vertex) that visits each edge exactly once? Euler mathematical proof, proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an parity (mathematics), even degree (graph theory), degree, and stated without proof that connectivity (graph theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Online Algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from the beginning and is required to output an answer which solves the problem at hand. In operations research Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ..., the area in which online algorithms are developed is called online optimization. As an example, consider the sorting algorithms selection sort and insertion sort: selection sort repeatedly selects the minimum element from the unsorted remainder and places it at the front, which requires access to the entire input; it is thus a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
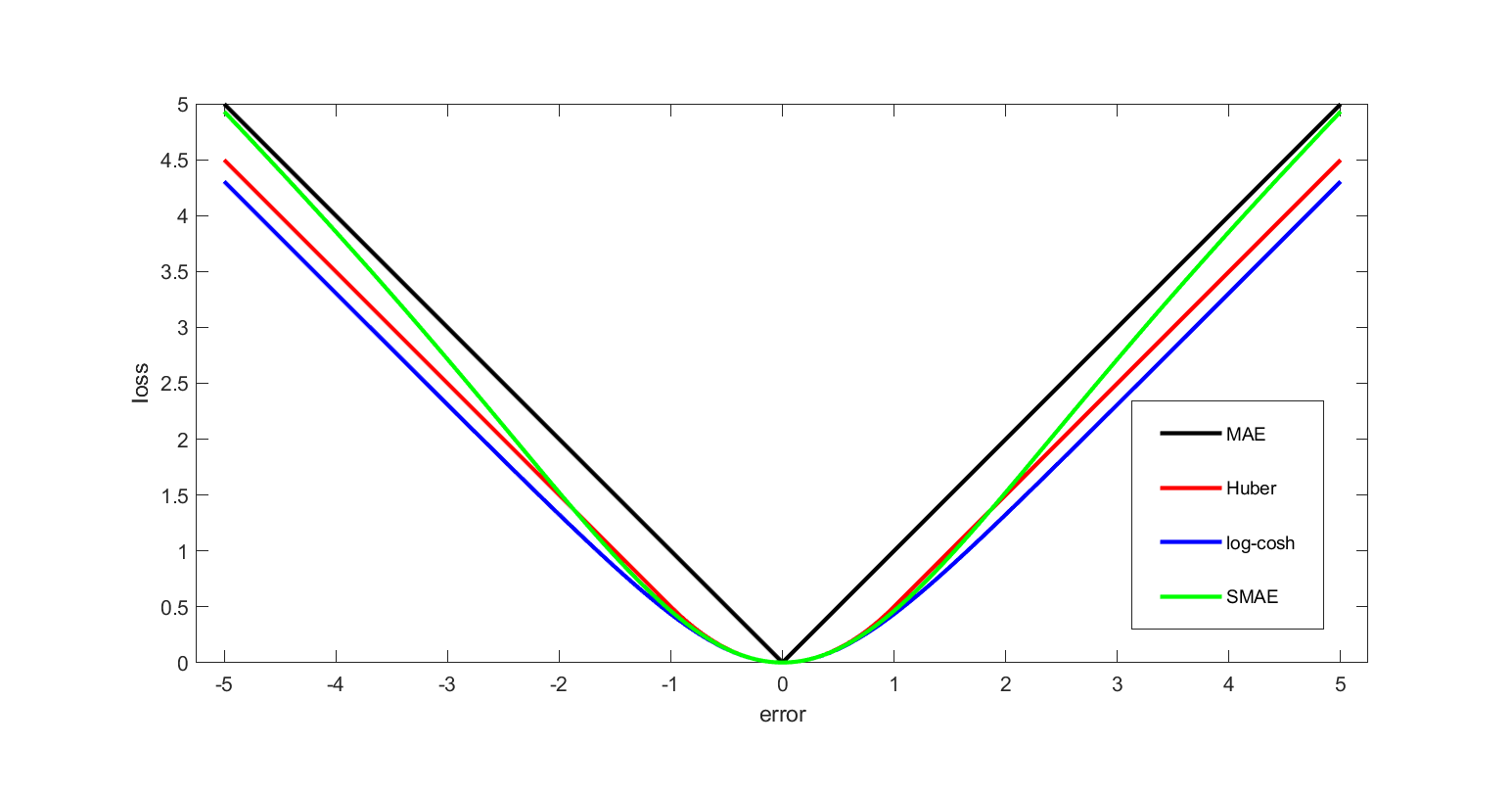
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Competitive Analysis (online Algorithm)
Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm (which must satisfy an unpredictable sequence of requests, completing each request without being able to see the future) is compared to the performance of an optimal ''offline algorithm'' that can view the sequence of requests in advance. An algorithm is ''competitive'' if its ''competitive ratio''—the ratio between its performance and the offline algorithm's performance—is bounded. Unlike traditional worst-case analysis, where the performance of an algorithm is measured only for "hard" inputs, competitive analysis requires that an algorithm perform well both on hard and easy inputs, where "hard" and "easy" are defined by the performance of the optimal offline algorithm. For many algorithms, performance is dependent not only on the size of the inputs, but also on their values. For example, sorting an array of elements varies in difficulty depending on th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimax
Minimax (sometimes Minmax, MM or saddle point) is a decision rule used in artificial intelligence, decision theory, combinatorial game theory, statistics, and philosophy for ''minimizing'' the possible loss function, loss for a Worst-case scenario, worst case (''max''imum loss) scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty. Game theory In general games The maximin value is the highest value that the player can be sure to get without knowing the actions of the other players; equivalently, it is the lowest value the other players can force the player to receive when they know the player's action. Its formal definition is: :\underline = \max_ \min_ W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |