|
Schmidt Decomposition
In linear algebra, the Schmidt decomposition (named after its originator Erhard Schmidt) refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has numerous applications in quantum information theory, for example in entanglement characterization and in state purification, and plasticity. Theorem Let H_1 and H_2 be Hilbert spaces of dimensions ''n'' and ''m'' respectively. Assume n \geq m. For any vector w in the tensor product H_1 \otimes H_2, there exist orthonormal sets \ \subset H_1 and \ \subset H_2 such that w= \sum_ ^m \alpha _i u_i \otimes v_i, where the scalars \alpha_i are real, non-negative, and unique up to re-ordering. Proof The Schmidt decomposition is essentially a restatement of the singular value decomposition in a different context. Fix orthonormal bases \ \subset H_1 and \ \subset H_2. We can identify an elementary tensor e_i \otimes f_j with the matrix e_i f_j ^\mathsf, where f_j ^\mathsf is the transpos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Partial Trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace (linear algebra), trace. Whereas the trace is a scalar (mathematics), scalar-valued function on operators, the partial trace is an operator (mathematics), operator-valued function. The partial trace has applications in quantum information and decoherence which is relevant for quantum measurement and thereby to the decoherent approaches to interpretations of quantum mechanics, including consistent histories and the relative state interpretation. Details Suppose V, W are finite-dimensional vector spaces over a field (mathematics), field, with dimensions m and n, respectively. For any space , let L(A) denote the space of linear operators on A. The partial trace over W is then written as , where \otimes denotes the Kronecker product. It is defined as follows: For , let , and , be bases for ''V'' and ''W'' respectively; then ''T'' has a matrix representation : \ \quad 1 \leq k, i \leq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Purification Of Quantum State
In quantum information theory, quantum state purification refers to the process of representing a mixed state as a pure quantum state of higher-dimensional Hilbert space. The purification allows the original mixed state to be recovered by taking the partial trace over the additional degrees of freedom. The purification is not unique, the different purifications that can lead to the same mixed states are limited by the Schrödinger–HJW theorem. Purification is used in algorithms such as entanglement distillation, magic state distillation and algorithmic cooling. Description Let \mathcal H_S be a finite-dimensional complex Hilbert space, and consider a generic (possibly mixed) quantum state \rho defined on \mathcal H_S and admitting a decomposition of the form \rho = \sum_i p_i, \phi_i\rangle\langle\phi_i, for a collection of (not necessarily mutually orthogonal) states , \phi_i\rangle \in \mathcal H_S and coefficients p_i \ge 0 such that \sum_i p_i = 1. Note that any quan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Singular Value Decomposition
In linear algebra, the singular value decomposition (SVD) is a Matrix decomposition, factorization of a real number, real or complex number, complex matrix (mathematics), matrix into a rotation, followed by a rescaling followed by another rotation. It generalizes the eigendecomposition of a square normal matrix with an orthonormal eigenbasis to any matrix. It is related to the polar decomposition#Matrix polar decomposition, polar decomposition. Specifically, the singular value decomposition of an m \times n complex matrix is a factorization of the form \mathbf = \mathbf, where is an complex unitary matrix, \mathbf \Sigma is an m \times n rectangular diagonal matrix with non-negative real numbers on the diagonal, is an n \times n complex unitary matrix, and \mathbf V^* is the conjugate transpose of . Such decomposition always exists for any complex matrix. If is real, then and can be guaranteed to be real orthogonal matrix, orthogonal matrices; in such contexts, the SVD ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Spin (physics)
Spin is an Intrinsic and extrinsic properties, intrinsic form of angular momentum carried by elementary particles, and thus by List of particles#Composite particles, composite particles such as hadrons, atomic nucleus, atomic nuclei, and atoms. Spin is quantized, and accurate models for the interaction with spin require relativistic quantum mechanics or quantum field theory. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The relativistic spin–statistics theorem connects electron spin quantization to the Pauli exclusion principle: observations of exclusion imply half-integer spin, and observations of half-integer spin imply exclusion. Spin is described mathematically as a vector for some particles such as photons, and as a spinor or bispinor for other particles such as electrons. Sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
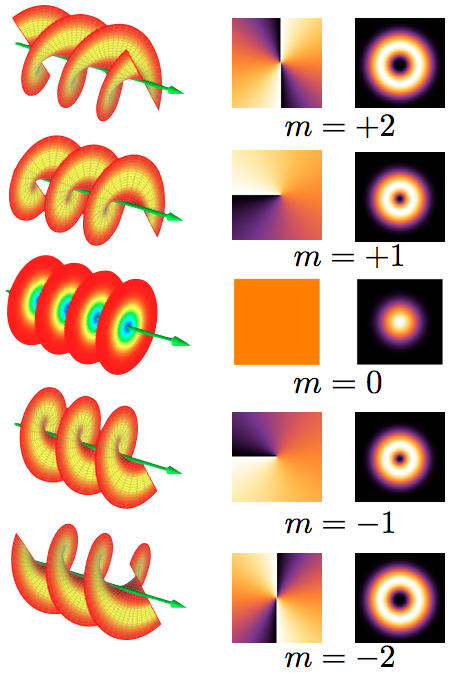 |
Orbital Angular Momentum Of Light
The orbital angular momentum of light (OAM) is the component of angular momentum of a light beam that is dependent on the field spatial distribution, and not on the polarization. OAM can be split into two types. The ''internal OAM'' is an origin-independent angular momentum of a light beam that can be associated with a helical or twisted wavefront. The ''external OAM'' is the origin-dependent angular momentum that can be obtained as cross product of the light beam position (center of the beam) and its total linear momentum. Concept A beam of light carries a linear momentum \mathbf, and hence it can be also attributed an external angular momentum \mathbf_e=\mathbf\times\mathbf. This external angular momentum depends on the choice of the origin of the coordinate system. If one chooses the origin at the beam axis and the beam is cylindrically symmetric (at least in its momentum distribution), the external angular momentum will vanish. The external angular momentum is a form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Qudit
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, one of the simplest quantum systems displaying the peculiarity of quantum mechanics. Examples include the spin of the electron in which the two levels can be taken as spin up and spin down; or the polarization of a single photon in which the two spin states (left-handed and the right-handed circular polarization) can also be measured as horizontal and vertical linear polarization. In a classical system, a bit would have to be in one state or the other. However, quantum mechanics allows the qubit to be in a coherent superposition of multiple states simultaneously, a property that is fundamental to quantum mechanics and quantum computing. Etymology The coining of the term ''qubit'' is attributed to Benjamin Schumacher. In the acknowledgmen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics ( electromagnetic ten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Multipartite Entanglement
In the case of systems composed of m > 2 subsystems, the classification of quantum-entangled states is richer than in the bipartite case. Indeed, in multipartite entanglement apart from fully separable states and fully entangled states, there also exists the notion of partially separable states. Full and partial separability The definitions of fully separable and fully entangled multipartite states naturally generalizes that of separable and entangled states in the bipartite case, as follows. Full ''m''-partite separability (''m''-separability) of ''m'' systems The state \; \varrho_ of \; m subsystems \; A_1, \ldots, A_m with Hilbert space \; \mathcal_=\mathcal_\otimes\ldots\otimes \mathcal_ is fully separable if and only if it can be written in the form :\; \varrho_ = \sum_^k p_i \varrho_^i \otimes \ldots \otimes \varrho_^i. Correspondingly, the state \; \varrho_ is fully entangled if it cannot be written in the above form. As in the bipartite case, the set of \; m-sep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Von Neumann Entropy
In physics, the von Neumann entropy, named after John von Neumann, is a measure of the statistical uncertainty within a description of a quantum system. It extends the concept of Gibbs entropy from classical statistical mechanics to quantum statistical mechanics, and it is the quantum counterpart of the Shannon entropy from classical information theory. For a quantum-mechanical system described by a density matrix , the von Neumann entropy is S = - \operatorname(\rho \ln \rho), where \operatorname denotes the trace and \operatorname denotes the matrix version of the natural logarithm. If the density matrix is written in a basis of its eigenvectors , 1\rangle, , 2\rangle, , 3\rangle, \dots as \rho = \sum_j \eta_j \left, j \right\rang \left\lang j \ , then the von Neumann entropy is merely S = -\sum_j \eta_j \ln \eta_j . In this form, ''S'' can be seen as the Shannon entropy of the eigenvalues, reinterpreted as probabilities. The von Neumann entropy and quantities based upon i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Separable State
In quantum mechanics, separable states are multipartite quantum states that can be written as a convex combination of product states. Product states are multipartite quantum states that can be written as a tensor product of states in each space. The physical intuition behind these definitions is that product states have no correlation between the different degrees of freedom, while separable states might have correlations, but all such correlations can be explained as due to a classical random variable, as opposed to being due to entanglement. In the special case of pure states the definition simplifies: a pure state is separable if and only if it is a product state. A state is said to be entangled if it is not separable. In general, determining if a state is separable is not straightforward and the problem is classed as NP-hard. Separability of bipartite systems Consider first composite states with two degrees of freedom, referred to as ''bipartite states''. By a postulate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |