|
Rössler Attractor
The Rössler attractor () is the attractor for the Rössler system, a system of three non-linear ordinary differential equations originally studied by Otto Rössler in the 1970s... These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor.. Rössler interpreted it as a formalization of a taffy-pulling machine. Some properties of the Rössler system can be deduced via linear methods such as eigenvectors, but the main features of the system require non-linear methods such as Poincaré maps and bifurcation diagrams. The original Rössler paper states the Rössler attractor was intended to behave similarly to the Lorenz attractor, but also be easier to analyze qualitatively. An orbit within the attractor follows an outward spiral close to the x, y plane around an unstable fixed point. Once the graph spirals out enough, a second fixed point influences the graph, causing a rise and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edward Lorenz
Edward Norton Lorenz (May 23, 1917 – April 16, 2008) was an American mathematician and meteorologist who established the theoretical basis of weather and climate predictability, as well as the basis for computer-aided atmospheric physics and meteorology. He is best known as the founder of modern chaos theory, a branch of mathematics focusing on the behavior of dynamical systems that are highly sensitive to initial conditions. His discovery of deterministic chaos "profoundly influenced a wide range of basic sciences and brought about one of the most dramatic changes in mankind's view of nature since Sir Isaac Newton," according to the committee that awarded him the 1991 Kyoto Prize for basic sciences in the field of earth and planetary sciences. Early life Lorenz was born in 1917 in West Hartford, Connecticut. He acquired an early love of science from both sides of his family. His father, Edward Henry Lorenz (1882-1956), majored in mechanical engineering at the Massachusetts I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roessler Attractor
Roessler is a surname. Notable people with the surname include: * Carol Roessler (born 1948), American politician * Henri Roessler (1910–1978), French football player and manager * Kira Roessler (born 1962), American bass guitarist, singer and Emmy award-winning dialogue editor * Oscar F. Roessler (1860-1932), American politician * Pat Roessler, American baseball coach * Paul Roessler (born 1958), American punk rock musician * Rudolf Roessler (1897–1958), German spy for the Soviet Union See also * Rößler * Rössler * Roeseler Roeseler or Röseler is a surname. Notable people with the surname include: * Larry Roeseler, American motorcycle racer * Fritz Roeseler (1897–1985), American football player * Nils Röseler (born 1992), German professional footballer See als ... * Bridgeport Roesslers {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaotic Attractor
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented algebraically as an ''n''-dimensional vector. The attractor is a region in ''n''-dimensional space. In physical systems, the ''n'' dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically ( fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable values with a solid line and unstable values with a dotted line, although often the unstable points are omitted. Bifurcation diagrams enable the visualization of bifurcation theory. In the context of discrete-time dynamical systems, the diagram is also called orbit diagram. Logistic map An example is the bifurcation diagram of the logistic map: x_=rx_n(1-x_n). The bifurcation parameter ''r'' is shown on the horizontal axis of the plot and the vertical axis shows the set of values of the logistic function visited asymptotically from almost all initial conditions. The bifurcation diagram shows the forking of the periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hénon Map
In mathematics, the Hénon map, sometimes called Hénon–Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaos theory, chaotic behavior. The Hénon map takes a point in the plane and maps it to a new point :\beginx_ = 1 - a x_n^2 + y_n\\y_ = b x_n.\end The map depends on two parameters, and , which for the classical Hénon map have values of and . For the classical values the Hénon map is chaotic. For other values of and the map may be Randomness, chaotic, Intermittency, intermittent, or converge to a periodic orbit. An overview of the type of behavior of the map at different parameter values may be obtained from its orbit diagram. The map was introduced by Michel Hénon as a simplified model of the Poincaré map, Poincaré section of the Lorenz attractor, Lorenz model. For the classical map, an initial point of the plane will either approach a set of points known as the Hénon Attrac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tent Map
In mathematics, the tent map with parameter μ is the real-valued function ''f''μ defined by :f_\mu(x) := \mu\min\, the name being due to the tent-like shape of the graph of ''f''μ. For the values of the parameter μ within 0 and 2, ''f''μ maps the unit interval , 1into itself, thus defining a discrete-time dynamical system on it (equivalently, a recurrence relation). In particular, iterating a point ''x''0 in , 1gives rise to a sequence x_n: :x_ = f_\mu(x_n) = \begin \mu x_n & \mathrm~~ x_n . The \mu = 2 case of the tent map is the present case of a= \tfrac. A sequence will have the same autocorrelation function as will data from the first-order autoregressive process In statistics, econometrics, and signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it can be used to describe certain time-varying processes in nature, economics, behavior, etc. The autoregre ... w_ = (2a-1)w_n + u_ with in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
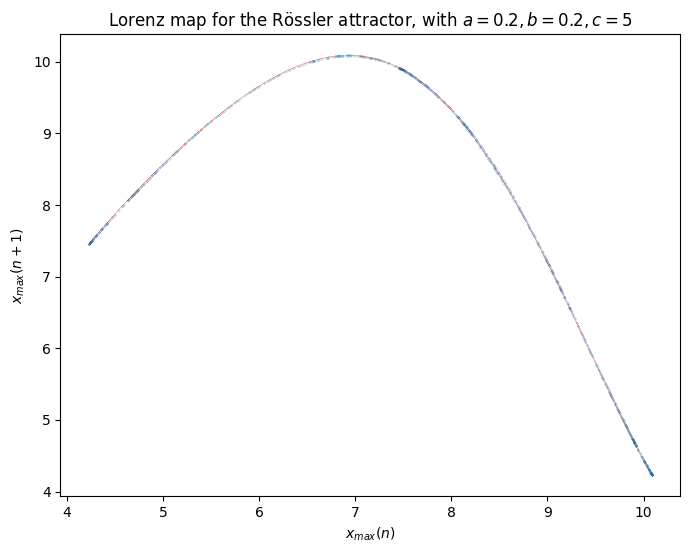
Lorenz Map For The Rossler Attractor
Lorenz is an originally German name derived from the Roman surname Laurentius, which means "from Laurentum". Given name People with the given name Lorenz include: * Prince Lorenz of Belgium (born 1955), member of the Belgian royal family by his marriage with Princess Astrid of Belgium * Lorenz Böhler (1885–1973), Austrian trauma surgeon * Lorenz Hart (1895–1943), American lyricist, half of the famed Broadway songwriting team Rodgers and Hart * Lorenz Lange (1690–1752), Russian official in Siberia * Lorenz Oken (1779–1851), German naturalist * Lorenz of Werle (1338/40–1393/94), Lord of Werle-Güstrow Surname People with the name surname Lorenz include: * Adolf Lorenz (1854–1946), Austrian surgeon * Alfred Lorenz (1868–1939), Austrian-German musical analyst * Angela Lorenz (born 1965), American artist * Barbara Lorenz, make-up artist * Carl Lorenz (1913–1993), German cyclist * Christian Lorenz (born 1966), German musician * Edward Norton Lorenz (1917–2008) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a Vector (mathematics and physics), vector that has its direction (geometry), direction unchanged (or reversed) by a given linear map, linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scalar multiplication, scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative number, negative or complex number, complex number). Euclidean vector, Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation Rotation (mathematics), rotates, Scaling (geometry), stretches, or Shear mapping, shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with nei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |