|
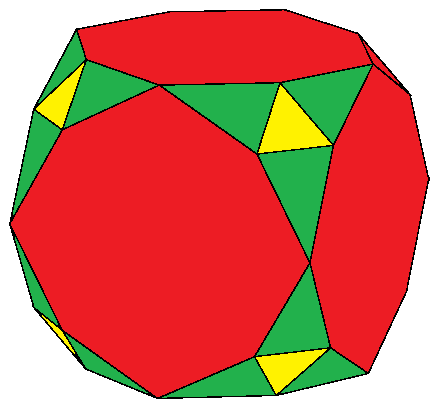
Rectified Truncated Cube
In geometry, the rectified truncated cube is a polyhedron, constructed as a rectified, truncated cube. It has 38 faces: 8 equilateral triangles, 24 isosceles triangles, and 6 octagons. Topologically, the triangles corresponding to the cube's vertices are always equilateral, although the octagons, while having equal edge lengths, do not have the same edge lengths with the equilateral triangles, having different but alternating angles, causing the other triangles to be isosceles instead. Related polyhedra The ''rectified truncated cube'' can be seen in sequence of rectification and truncation operations from the cube. Further truncation, and alternation operations creates two more polyhedra: See also * Rectified truncated tetrahedron * Rectified truncated octahedron * Rectified truncated dodecahedron * Rectified truncated icosahedron References * Coxeter '' Regular Polytopes'', Third edition, (1973), Dover edition, (pp. 145–154 Chapter 8: Truncation) * John H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle. Principal properties Denoting the common length of the sides of the equilateral triangle as a, we can determine using the Pythagorean theorem that: *The area is A=\frac a^2, *The perimeter is p=3a\,\! *The radius of the circumscribed circle is R = \frac *The radius of the inscribed circle is r=\frac a or r=\frac *The geometric center of the triangle is the center of the circumscribed and inscribed circles *The altitude (height) from any side is h=\frac a Denoting the radius of the circumscribed circle as ''R'', we can determine using trigonometry that: *The area of the triangle is \mathrm=\fracR^2 Many of these quantities have simple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
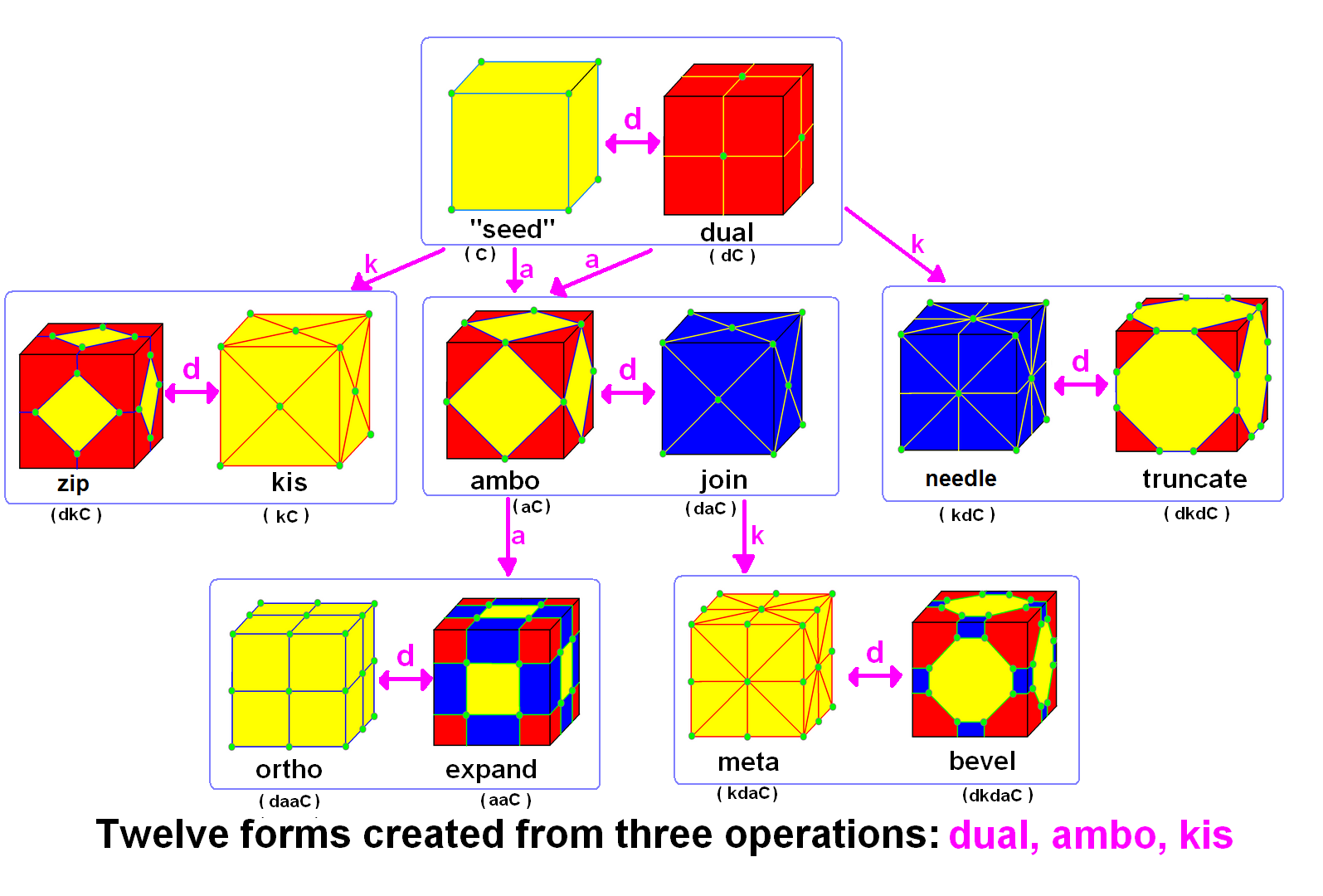
Conway Polyhedron Notation
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is (topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), (snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the Archimedean and Cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life. Born and raised in Liverpool, Conway spent the first half of his career at the University of Cambridge before moving to the United States, where he held the John von Neumann Professorship at Princeton University for the rest of his career. On 11 April 2020, at age 82, he died of complications from COVID-19. Early life and education Conway was born on 26 December 1937 in Liverpool, the son of Cyril Horton Conway and Agnes Boyce. He became interested in mathematics at a very early age. By the time he was 11, his ambition was to become a mathematician. After leaving sixth form, he studied mathematics at Gonville and Caius College ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Polytopes (book)
''Regular Polytopes'' is a geometry book on regular polytopes written by Harold Scott MacDonald Coxeter. It was originally published by Methuen in 1947 and by Pitman Publishing in 1948, with a second edition published by Macmillan in 1963 and a third edition by Dover Publications in 1973. The Basic Library List Committee of the Mathematical Association of America has recommended that it be included in undergraduate mathematics libraries. Overview The main topics of the book are the Platonic solids (regular convex polyhedra), related polyhedra, and their higher-dimensional generalizations. It has 14 chapters, along with multiple appendices, providing a more complete treatment of the subject than any earlier work, and incorporating material from 18 of Coxeter's own previous papers. It includes many figures (both photographs of models by Paul Donchian and drawings), tables of numerical values, and historical remarks on the subject. The first chapter discusses regular polygons, regu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harold Scott MacDonald Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Truncated Icosahedron
In geometry, the rectified truncated icosahedron is a convex polyhedron. It has 92 faces: 60 isosceles triangles, 12 regular pentagons, and 20 regular hexagons. It is constructed as a rectified, truncated icosahedron, rectification truncating vertices down to mid-edges. As a near-miss Johnson solid, under icosahedral symmetry, the pentagons are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the pentagons, having slightly different but alternating angles, causing the triangles to be isosceles instead. The shape is a symmetrohedron with notation ''I(1,2,*, '' Images Dual By Conway polyhedron notation, the dual polyhedron can be called a ''joined truncated icosahedron'', jtI, but it is topologically equivalent to the rhombic enneacontahedron with all rhombic faces. Related polyhedra The ''rectified truncated icosahedron'' can be seen in sequence of rectification and truncation operations from the truncated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Truncated Dodecahedron
In geometry, the rectified truncated dodecahedron is a convex polyhedron, constructed as a rectified, truncated dodecahedron. It has 92 faces: 20 equilateral triangles, 60 isosceles triangles, and 12 decagons. Topologically, the triangles corresponding to the dodecahedrons's vertices are always equilateral, although the decagons, while having equal edge lengths, do not have the same edge lengths with the equilateral triangles, having different but alternating angles, causing the other triangles to be isosceles instead. Related polyhedra The ''rectified truncated dodecahedron'' can be seen in sequence of rectification and truncation operations from the dodecahedron. Further truncation, and alternation operations creates two more polyhedra: See also * Rectified truncated tetrahedron * Rectified truncated octahedron * Rectified truncated cube * Rectified truncated icosahedron References * Coxeter '' Regular Polytopes'', Third edition, (1973), Dover edition, (pp.& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Truncated Octahedron
In geometry, the rectified truncated octahedron is a convex polyhedron, constructed as a Rectification (geometry), rectified, truncated octahedron. It has 38 faces: 24 isosceles triangles, 6 squares, and 8 hexagons. Topologically, the squares corresponding to the octahedron's vertices are always regular, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the squares, having different but alternating angles, causing the triangles to be Isosceles triangle, isosceles instead. Related polyhedra The ''rectified truncated octahedron'' can be seen in sequence of rectification (geometry), rectification and truncation (geometry), truncation operations from the octahedron. Further truncation, and alternation (geometry), alternation creates two more polyhedra: See also * Rectified truncated tetrahedron * Rectified truncated cube * Rectified truncated dodecahedron * Rectified truncated icosahedron References * Harold Scott MacDonald Coxeter, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Truncated Tetrahedron
In geometry, the rectified truncated tetrahedron is a polyhedron, constructed as a Rectification (geometry), rectified, truncated tetrahedron. It has 20 faces: 4 equilateral triangles, 12 isosceles triangles, and 4 regular hexagons. Topologically, the triangles corresponding to the tetrahedron's vertices are always equilateral, although the hexagons, while having equal edge lengths, do not have the same edge lengths with the equilateral triangles, having different but alternating angles, causing the other triangles to be Isosceles triangle, isosceles instead. Related polyhedra The ''rectified truncated tetrahedron'' can be seen in sequence of rectification (geometry), rectification and truncation (geometry), truncation operations from the tetrahedron. Further truncation, and alternation (geometry), alternation operations creates two more polyhedra: See also * Rectified truncated cube * Rectified truncated octahedron * Rectified truncated dodecahedron * Rectified truncated ic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snub Rectified Truncated Cube
A snub, cut or slight is a refusal to recognise an acquaintance by ignoring them, avoiding them or pretending not to know them. For example, a failure to greeting, greet someone may be considered a snub. In Awards and Lists For awards, the term "snub" is usually used to refer to a work or person that fails to be nominated or win award, with whether or not a person or work was legitimately snubbed for an award has often been subject for public debate. The term Snub has also been used in relation to lists, such as the NBA 75th Anniversary Team. Many of the most notable people and works have failed to be nominated or win a major award for example Alfred Hitchcock, Stanley Kubrick, and Spike Lee never won best director at the Oscars despite being nominated five, four, and one time respectively, Glenn Close, Peter O'Toole, and Cicely Tyson were also notable for having never won an Oscar related to acting despite each of them having multiple nominations. Among films, ''Citizen Kane'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Rectified Truncated Cube
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones. Truncation may also refer to: Mathematics * Truncation (statistics) refers to measurements which have been cut off at some value * Truncation (numerical analysis) refers to truncating an infinite sum by a finite one * Truncation (geometry) is the removal of one or more parts, as for example in truncated cube * Propositional truncation, a type former which truncates a type down to a mere proposition Computer science * Data truncation, an event that occurs when a file or other data is stored in a location too small to accommodate its entire length * Truncate (SQL), a command in the SQL data manipulation language to quickly remove all data from a table Biology * Truncate, a leaf shape * Truncated protein, a protein shortened by a mutation which specifically induces premature termination of messenger RNA translation Other uses * Cheque truncation, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified Truncated Cube
In geometry, the rectified truncated cube is a polyhedron, constructed as a rectified, truncated cube. It has 38 faces: 8 equilateral triangles, 24 isosceles triangles, and 6 octagons. Topologically, the triangles corresponding to the cube's vertices are always equilateral, although the octagons, while having equal edge lengths, do not have the same edge lengths with the equilateral triangles, having different but alternating angles, causing the other triangles to be isosceles instead. Related polyhedra The ''rectified truncated cube'' can be seen in sequence of rectification and truncation operations from the cube. Further truncation, and alternation operations creates two more polyhedra: See also * Rectified truncated tetrahedron * Rectified truncated octahedron * Rectified truncated dodecahedron * Rectified truncated icosahedron References * Coxeter '' Regular Polytopes'', Third edition, (1973), Dover edition, (pp. 145–154 Chapter 8: Truncation) * John H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |