|
Physics (Aristotle)
The ''Physics'' (; or , possibly meaning " Lectures on nature") is a named text, written in ancient Greek, collated from a collection of surviving manuscripts known as the Corpus Aristotelicum, attributed to the 4th-century BC philosopher Aristotle. The meaning of physics in Aristotle It is a collection of treatises or lessons that deals with the most general (philosophical) principles of natural or moving things, both living and non-living, rather than physical theories (in the modern sense) or investigations of the particular contents of the universe. The chief purpose of the work is to discover the principles and causes of (and not merely to describe) change, or movement, or motion (κίνησις ''kinesis''), especially that of natural wholes (mostly living things, but also inanimate wholes like the cosmos). In the conventional Andronicean ordering of Aristotle's works, it stands at the head of, as well as being foundational to, the long series of physical, cosmolog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristotle Physica Page 1
Aristotle (; 384–322 BC) was an Ancient Greek philosophy, Ancient Greek philosopher and polymath. His writings cover a broad range of subjects spanning the natural sciences, philosophy, linguistics, economics, politics, psychology, and the arts. As the founder of the Peripatetic school of philosophy in the Lyceum (classical), Lyceum in Athens, he began the wider Aristotelianism, Aristotelian tradition that followed, which set the groundwork for the development of modern science. Little is known about Aristotle's life. He was born in the city of Stagira (ancient city), Stagira in northern Greece during the Classical Greece, Classical period. His father, Nicomachus (father of Aristotle), Nicomachus, died when Aristotle was a child, and he was brought up by a guardian. At around eighteen years old, he joined Plato's Platonic Academy, Academy in Athens and remained there until the age of thirty seven (). Shortly after Plato died, Aristotle left Athens and, at the request ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomism
Atomism () is a natural philosophy proposing that the physical universe is composed of fundamental indivisible components known as atoms. References to the concept of atomism and its Atom, atoms appeared in both Ancient Greek philosophy, ancient Greek and Ancient Indian philosophy, ancient Indian philosophical traditions. Leucippus is the earliest figure whose commitment to atomism is well attested and he is usually credited with inventing atomism. He and other ancient Greek atomists theorized that nature consists of two fundamental Principle (philosophy), principles: ''atom'' and Void (philosophy), ''void''. Clusters of different shapes, arrangements, and positions give rise to the various macroscopic Substance (philosophy), substances in the world.Berryman, Sylvia, "Ancient Atomism", ''Stanford Encyclopedia of Philosophy, The Stanford Encyclopedia of Philosophy'' (Fall 2008 Edition), Edward N. Zalta (ed.)online/ref> Indian Buddhists, such as Dharmakirti ( 6th or 7th century) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeno Of Elea
Zeno of Elea (; ; ) was a pre-Socratic Greek philosopher from Elea, in Southern Italy (Magna Graecia). He was a student of Parmenides and one of the Eleatics. Zeno defended his instructor's belief in monism, the idea that only one single entity exists that makes up all of reality. He rejected the existence of space, time, and motion. To disprove these concepts, he developed a series of paradoxes to demonstrate why they are impossible. Though his original writings are lost, subsequent descriptions by Plato, Aristotle, Diogenes Laertius, and Simplicius of Cilicia have allowed study of his ideas. Zeno's arguments are divided into two different types: his arguments against plurality, or the existence of multiple objects, and his arguments against motion. Those against plurality suggest that for anything to exist, it must be divisible infinitely, meaning it would necessarily have both infinite mass and no mass simultaneously. Those against motion invoke the idea that distance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
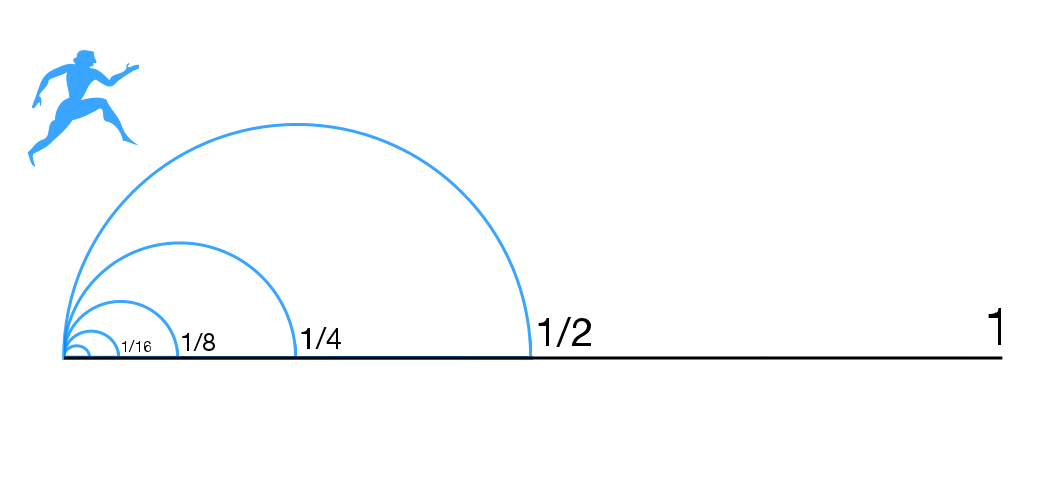
Zeno's Paradoxes
Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno devised these paradoxes to support his teacher Parmenides's philosophy of monism, which posits that despite people's sensory experiences, reality is singular and unchanging. The paradoxes famously challenge the notions of plurality (the existence of many things), motion, space, and time by suggesting they lead to logical contradictions. Zeno's work, primarily known from second-hand accounts since his original texts are lost, comprises forty "paradoxes of plurality," which argue against the coherence of believing in multiple existences, and several arguments against motion and change. Of these, only a few are definitively known today, including the renowned "Achilles Paradox", which illustrates the problematic concept of infinite divisibi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
On Generation And Corruption
''On Generation and Corruption'' (; ), also known as ''On Coming to Be and Passing Away'' is a treatise by Aristotle. Like many of his texts, it is both scientific, part of Aristotle's biology, and philosophic. The philosophy is essentially empirical; as in all of Aristotle's works, the inferences made about the unexperienced and unobservable are based on observations and real experiences. Overview The question raised at the beginning of the text builds on an idea from Aristotle's earlier work '' The Physics''. Namely, whether things come into being through causes, through some prime material, or whether everything is generated purely through "alteration." Alteration concerned itself with the ability for elements to change based on common and uncommon qualities. From this important work Aristotle gives us two of his most remembered contributions. First, the Four Causes and also the Four Elements (earth, wind, fire, and water). He uses these four elements to provide an ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Void (philosophy)
The concept of "The Void" in philosophy encompasses the ideas of nothingness and emptiness, a notion that has been interpreted and debated across various schools of metaphysics. In ancient Greek philosophy, the Void was discussed by thinkers like Democritus, who saw it as a necessary space for atoms to move, thereby enabling the existence of matter. Contrasting this, Aristotle famously denied the existence of a true Void, arguing that nature inherently avoids a vacuum. In Eastern philosophical traditions, the Void takes on significant spiritual and metaphysical meanings. In Buddhism, ''Śūnyatā'' refers to the emptiness inherent in all things, a fundamental concept in understanding the nature of reality. In Taoism, the Void is represented by '' Wuji'', the undifferentiated state from which all existence emerges, embodying both the potential for creation and the absence of form. Throughout the history of Western thought, the Void has also been explored in the context of existentia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Actual Infinity
In the philosophy of mathematics, the abstraction of actual infinity, also called completed infinity, involves infinite entities as given, actual and completed objects. The concept of actual infinity was introduced into mathematics near the end of the 19th century by Georg Cantor with his theory of infinite sets, and was later formalized into Zermelo–Fraenkel set theory. This theory, which is presently commonly accepted as a foundation of mathematics, contains the axiom of infinity, which means that the natural numbers form a set (necessarily infinite). A great discovery of Cantor is that, if one accepts infinite sets, then there are different sizes ( cardinalities) of infinite sets, and, in particular, the cardinal of the continuum of the real numbers is strictly larger than the cardinal of the natural numbers. Actual infinity is to be contrasted with potential infinity, in which an endless process (such as "add 1 to the previous number") produces a sequence with no last el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potentiality And Actuality (Aristotle)
In philosophy, potentiality and actuality are a pair of closely connected principles which Aristotle used to analyze motion, causality, ethics, and physiology in his ''Physics'', ''Metaphysics'', ''Nicomachean Ethics'', and ''De Anima''. The concept of potentiality, in this context, generally refers to any "possibility" that a thing can be said to have. Aristotle did not consider all possibilities the same, and emphasized the importance of those that become real of their own accord when conditions are right and nothing stops them. Actuality, in contrast to potentiality, is the motion, change or activity that represents an exercise or fulfillment of a possibility, when a possibility becomes real in the fullest sense. Both these concepts therefore reflect Aristotle's belief that events in nature are not all natural in a true sense. As he saw it, many things happen accidentally, and therefore not according to the natural purposes of things. These concepts, in modified forms, rema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Teleology
Teleology (from , and )Partridge, Eric. 1977''Origins: A Short Etymological Dictionary of Modern English'' London: Routledge, p. 4187. or finalityDubray, Charles. 2020 912Teleology. In ''The Catholic Encyclopedia'' 14. New York: Robert Appleton Company. Retrieved 3 May 2020. – via '' New Advent'', transcribed by D. J. Potter is a branch of causality giving the reason or an explanation for something as a function of its end, its purpose, or its goal, as opposed to as a function of its cause. James Wood, in his '' Nuttall Encyclopaedia'', explained the meaning of ''teleology'' as "the doctrine of final causes, particularly the argument for the being and character of God from the being and character of His works; that the end reveals His purpose from the beginning, the end being regarded as the thought of God at the beginning, or the universe viewed as the realisation of Him and His eternal purpose." A purpose that is imposed by human use, such as the purpose of a fork to hold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telos (philosophy)
Telos (; ) is a term used by philosopher Aristotle to refer to the final cause of a natural organ or entity, or of human art. ''Telos'' is the root of the modern term teleology, the study of purposiveness or of objects with a view to their aims, purposes, or intentions. Teleology is central in Aristotle's work on plant and animal biology, and human ethics, through his theory of the four causes. Aristotle's notion that everything has a ''telos'' also gave rise to epistemology. In Aristotle ''Telos'' has been consistently used in the writings of Aristotle, in which the term, on several occasions, denotes 'goal'. It is considered synonymous to ''teleute'' ('end'), particularly in Aristotle's discourse about the plot-structure in '' Poetics''. The philosopher went as far as to say that ''telos'' can encompass all forms of human activity. One can say, for instance, that the ''telos'' of warfare is victory, or the ''telos'' of business is the creation of wealth. Within this conceptu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four Causes
The four causes or four explanations are, in Aristotelianism, Aristotelian thought, categories of questions that explain "the why's" of something that exists or changes in nature. The four causes are the: #Material, material cause, the #Formal, formal cause, the #Efficient, efficient cause, and the #Final, final cause. Aristotle wrote that "we do not have knowledge of a thing until we have grasped its why, that is to say, its cause." While there are cases in which classifying a "cause" is difficult, or in which "causes" might merge, Aristotle held that his four "causes" provided an analytical scheme of general applicability. Aristotle's word ''aitia'' () has, in philosophical scholarly tradition, been translated as 'cause'. This peculiar, specialized, technical, usage of the word 'cause' is not that of everyday English language. Rather, the translation of Aristotle's that is nearest to current ordinary language is "explanation." In ''Physics (Aristotle), Physics'' II.3 and ''Me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |