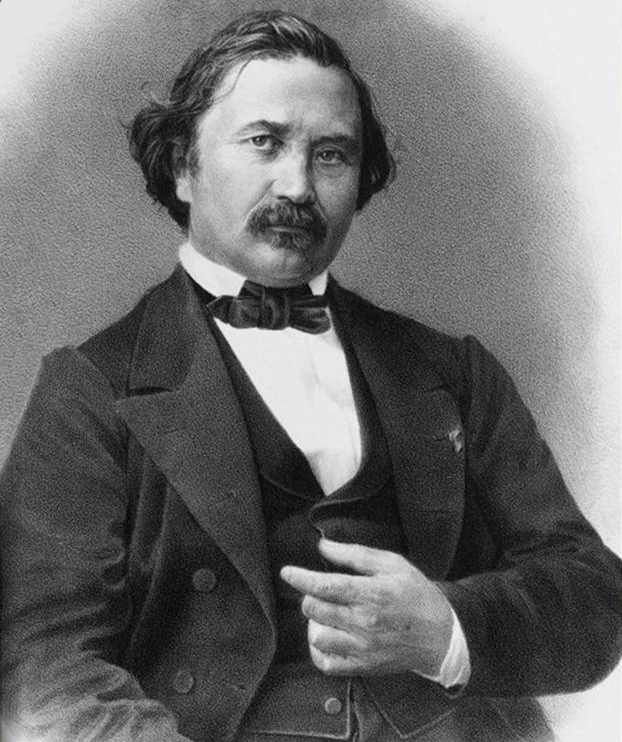|
Oppermann's Conjecture
Oppermann's conjecture is an unsolved problem in mathematics on the distribution of prime numbers.. It is closely related to but stronger than Legendre's conjecture, Andrica's conjecture, and Brocard's conjecture. It is named after Danish mathematician Ludvig Oppermann, who announced it in an unpublished lecture in March 1877. Statement The conjecture states that, for every integer n>1, there is at least one prime number between : n(n-1) and n^2, and at least another prime between : n^2 and n(n+1). It can also be phrased equivalently as stating that the prime-counting function must take unequal values at the endpoints of each range.. That is: : \pi(n^2-n)<\pi(n^2)<\pi(n^2+n) for every with being the number of prime numbers less than or equal to . The end points of these two ranges are a between tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in the triangular arrangement with dots on each side, and is equal to the sum of the natural numbers from 1 to . The first 100 terms sequence of triangular numbers, starting with the 0th triangular number, are Formula The triangular numbers are given by the following explicit formulas: where \textstyle is notation for a binomial coefficient. It represents the number of distinct pairs that can be selected from objects, and it is read aloud as " plus one choose two". The fact that the nth triangular number equals n(n+1)/2 can be illustrated using a visual proof. For every triangular number T_n, imagine a "half-rectangle" arrangement of objects corresponding to the triangular number, as in the figure below. Copying this arrangement ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number Theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic analysis, asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function). The first such distribution found is , where is the prime-counting function (the number of primes less than or equal to ''N'') and is the natural logarithm of . This means that for large enough , the probability that a random integer not greater than is prime is very close to . Consequently, a random integer with at most digits (for large enough ) is about half as likely to be prime as a random integer with at most digits. For example, among the positive integers of at most 1000 digits, about on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bertrand's Postulate
In number theory, Bertrand's postulate is the theorem that for any integer n > 3, there exists at least one prime number p with :n < p < 2n - 2. A less restrictive formulation is: for every , there is always at least one prime such that : Another formulation, where is the -th prime, is: for : This statement was first conjectured in 1845 by Joseph Bertrand (1822–1900). Bertrand himself verified his statement for all integers . His conjecture was completely Proof of Bertrand's postulate, proved by Pafnuty Chebyshev, Chebyshev (1821–1894) in 1852 and so the postulate is also called the Bertrand–Chebyshev theorem or Chebyshev's theorem. Chebyshev's theorem can also be stated as a relationship with , the prime-counting function (number of primes less than or equal to ): ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ulam Spiral
The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's ''Mathematical Games'' column in ''Scientific American'' a short time later. It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers. Ulam and Gardner emphasized the striking appearance in the spiral of prominent diagonal, horizontal, and vertical lines containing large numbers of primes. Both Ulam and Gardner noted that the existence of such prominent lines is not unexpected, as lines in the spiral correspond to quadratic polynomials, and certain such polynomials, such as Euler's prime-generating polynomial ''x''2 − ''x'' + 41, are believed to produce a high density of prime numbers. Nevertheless, the Ulam spiral is connected with major unsolved problems in number theory such as Landau's problems. In particular, no quadratic polynomial has ever ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Gap
A prime gap is the difference between two successive prime numbers. The ''n''-th prime gap, denoted ''g''''n'' or ''g''(''p''''n'') is the difference between the (''n'' + 1)-st and the ''n''-th prime numbers, i.e., :g_n = p_ - p_n. We have ''g''1 = 1, ''g''2 = ''g''3 = 2, and ''g''4 = 4. The sequence (''g''''n'') of prime gaps has been extensively studied; however, many questions and conjectures remain unanswered. The first 60 prime gaps are: :1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14, 4, 6, 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, 4, 2, 12, 12, 4, 2, 4, 6, 2, 10, 6, 6, 6, 2, 6, 4, 2, ... . By the definition of ''g''''n'' every prime can be written as :p_ = 2 + \sum_^n g_i. Simple observations The first, smallest, and only odd prime gap is the gap of size 1 between 2, the only even prime number, and 3, the first odd prime. All other prime gaps are even. There is only one pair of consecutive gaps having length 2: the gap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pronic Number
A pronic number is a number that is the product of two consecutive integers, that is, a number of the form n(n+1).. The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers,. or rectangular numbers; however, the term "rectangular number" has also been applied to the composite numbers. The first 60 pronic numbers are: : 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462, 506, 552, 600, 650, 702, 756, 812, 870, 930, 992, 1056, 1122, 1190, 1260, 1332, 1406, 1482, 1560, 1640, 1722, 1806, 1892, 1980, 2070, 2162, 2256, 2352, 2450, 2550, 2652, 2756, 2862, 2970, 3080, 3192, 3306, 3422, 3540, 3660... . Letting P_n denote the pronic number n(n+1), we have P_ = P_. Therefore, in discussing pronic numbers, we may assume that n\geq 0 without loss of generality, a convention that is adopted in the following sections. As figurate numbers The pronic numbers were studied as figurate nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degree (angle), degrees, or Pi, /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called square (algebra), squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime-counting Function
In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number . It is denoted by (unrelated to the number ). A symmetric variant seen sometimes is , which is equal to if is exactly a prime number, and equal to otherwise. That is, the number of prime numbers less than , plus half if equals a prime. Growth rate Of great interest in number theory is the growth rate of the prime-counting function. It was conjectured in the end of the 18th century by Gauss and by Legendre to be approximately \frac where is the natural logarithm, in the sense that \lim_ \frac=1. This statement is the prime number theorem. An equivalent statement is \lim_\frac=1 where is the logarithmic integral function. The prime number theorem was first proved in 1896 by Jacques Hadamard and by Charles de la Vallée Poussin independently, using properties of the Riemann zeta function introduced by Riemann in 1859. Proof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |