|
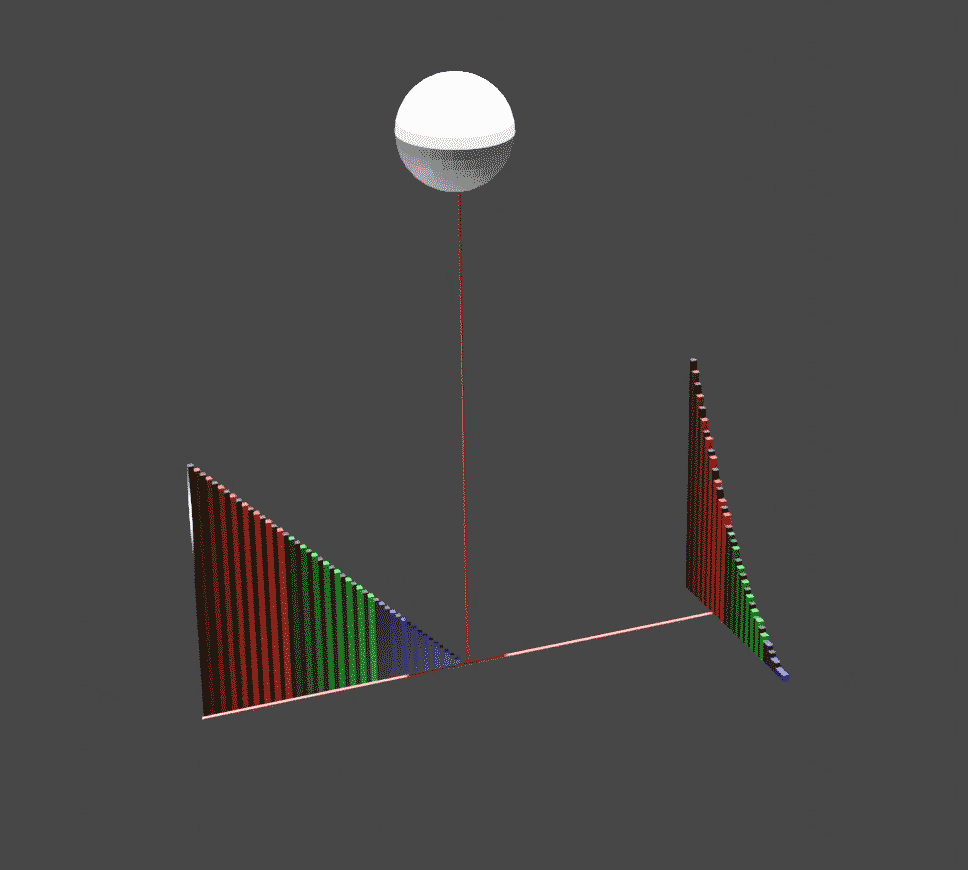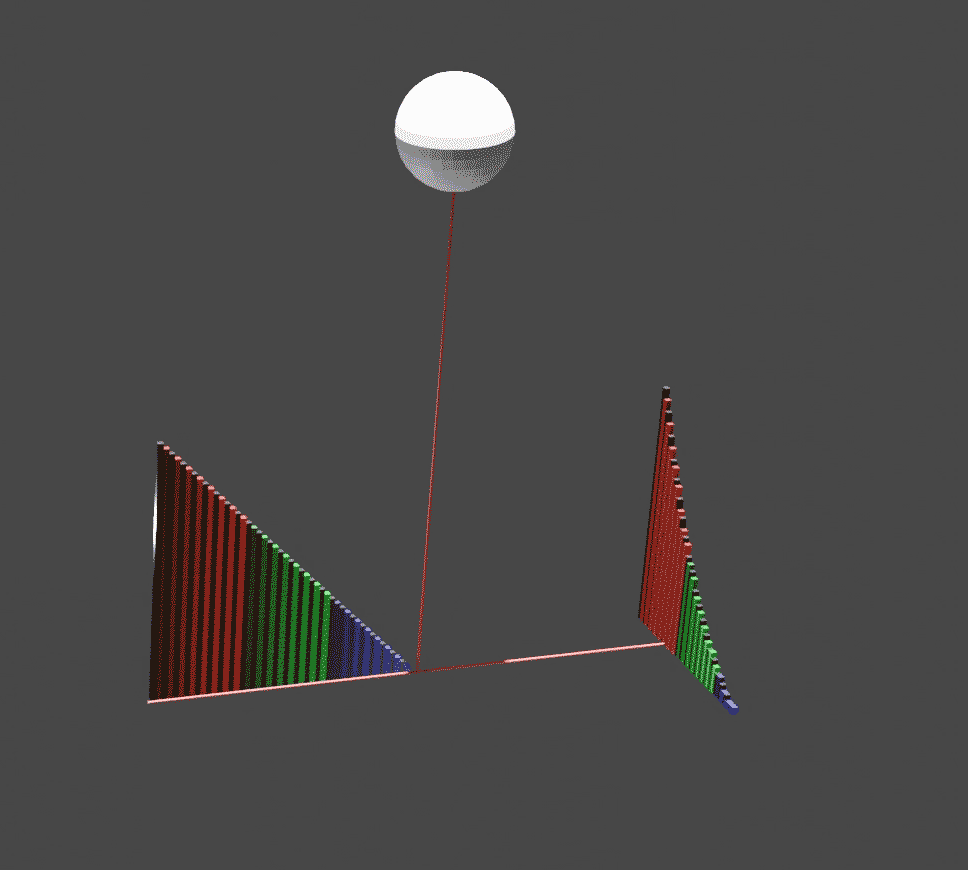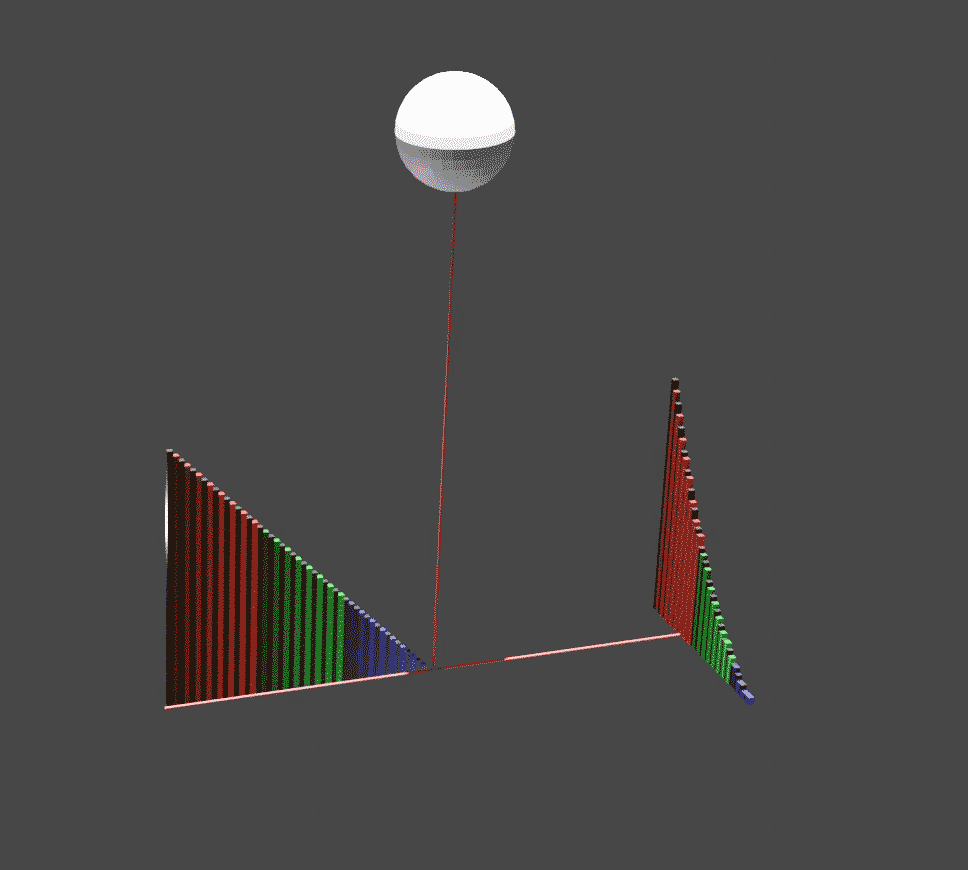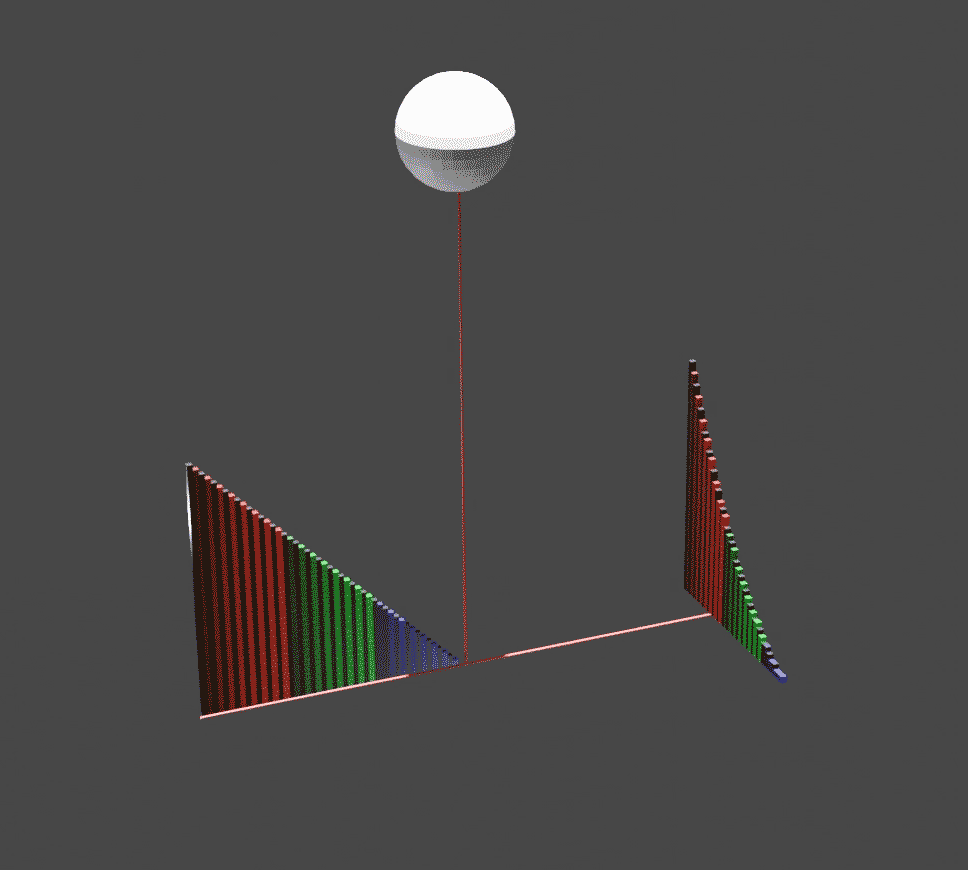
On The Sphere And Cylinder
''On the Sphere and Cylinder'' () is a treatise that was published by Archimedes in two volumes . It most notably details how to find the surface area of a sphere and the volume of the contained ball and the analogous values for a cylinder, and was the first to do so. Contents The principal formulae derived in ''On the Sphere and Cylinder'' are those mentioned above: the surface area of the sphere, the volume of the contained ball, and surface area and volume of the cylinder. Let r be the radius of the sphere and cylinder, and h be the height of the cylinder, with the assumption that the cylinder is a right cylinder—the side is perpendicular to both caps. In his work, Archimedes showed that the surface area of a cylinder is equal to: :A_C = 2 \pi r^2 + 2 \pi r h = 2 \pi r ( r + h ).\, and that the volume of the same is: :V_C = \pi r^2 h. \, On the sphere, he showed that the surface area is four times the area of its great circle. In modern terms, this means that the surf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes - On The Sphere And Cylinder
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cicero
Marcus Tullius Cicero ( ; ; 3 January 106 BC – 7 December 43 BC) was a Roman statesman, lawyer, scholar, philosopher, orator, writer and Academic skeptic, who tried to uphold optimate principles during the political crises that led to the establishment of the Roman Empire. His extensive writings include treatises on rhetoric, philosophy and politics. He is considered one of Rome's greatest orators and prose stylists and the innovator of what became known as "Ciceronian rhetoric". Cicero was educated in Rome and in Greece. He came from a wealthy municipal family of the Roman equestrian order, and served as consul in 63 BC. He greatly influenced both ancient and modern reception of the Latin language. A substantial part of his work has survived, and he was admired by both ancient and modern authors alike. Cicero adapted the arguments of the chief schools of Hellenistic philosophy in Latin and coined a large portion of Latin philosophical vocabulary via ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Editori Riuniti
Editori Riuniti is an Italian publishing house based in Rome that publishes books and magazines on the history of socialism, socialist thought, physics and mathematics theory, and the history of Central and Eastern Europe and the Balkans. History Editori Riuniti was founded in 1953 by the merger of the Italian Communist Party's two existing publishing houses, 's Edizioni Rinascita and 's Edizioni di Cultura Sociale. Bonchio became head of the new publishing house and initiated, in its first decade, a period of expansion. Editori Riuniti began publishing its flagship magazines, which were initially edited by Bonchio and Gerratana until Bruno Munari contributed to their graphic design. The publishing house also began important partnerships with European intellectuals like Maurice Dobb, Louis Althusser, Eric Hobsbawm, and Roberto Longhi. In the 1970s, Editori Riuniti published the ''Opere complete di Marx e Engels'' and the 11-volume encyclopedia ''Ulisse'', under the direction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylinder
A cylinder () has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base. A cylinder may also be defined as an infinite curvilinear surface in various modern branches of geometry and topology. The shift in the basic meaning—solid versus surface (as in a solid ball versus sphere surface)—has created some ambiguity with terminology. The two concepts may be distinguished by referring to solid cylinders and cylindrical surfaces. In the literature the unadorned term "cylinder" could refer to either of these or to an even more specialized object, the '' right circular cylinder''. Types The definitions and results in this section are taken from the 1913 text ''Plane and Solid Geometry'' by George A. Wentworth and David Eugene Smith . A ' is a surface consisting of all the points on all the lines which are parallel to a given line and which pass through a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Property
In abstract algebra and mathematical analysis, analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, Italy, Syracuse, is a property held by some algebraic structures, such as ordered or normed group (algebra), groups, and field (mathematics), fields. The property, as typically construed, states that given two positive numbers x and y, there is an integer n such that nx > y. It also means that the set of natural numbers is not bounded above. Roughly speaking, it is the property of having no ''infinitely large'' or ''infinitely small'' elements. It was Otto Stolz who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes’ ''On the Sphere and Cylinder''. The notion arose from the theory of magnitude (mathematics), magnitudes of ancient Greece; it still plays an important role in modern mathematics such as David Hilbert's Hilbert's axioms, axioms for geometry, and the theories of linearly ordered group, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Method Of Mechanical Theorems
''The Method of Mechanical Theorems'' (), also referred to as ''The Method'', is one of the major surviving works of the ancient Greece, ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of method of indivisibles, indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the Center of mass, center of weights of figures (centroid) and the Lever#Law of the lever, law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''. Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes Palimpsest
The Archimedes Palimpsest is a parchment codex palimpsest, originally a Byzantine Greek copy of a compilation of Archimedes and other authors. It contains two works of Archimedes that were thought to have been lost (the '' Ostomachion'' and the '' Method of Mechanical Theorems'') and the only surviving original Greek edition of his work '' On Floating Bodies''. The first version of the compilation is believed to have been produced by Isidore of Miletus, the architect of the geometrically complex Hagia Sophia cathedral in Constantinople, sometime around AD 530. The copy found in the palimpsest was created from this original, also in Constantinople, during the Macedonian Renaissance (c. AD 950), a time when mathematics in the capital was being revived by the former Greek Orthodox bishop of Thessaloniki Leo the Geometer, a cousin of the Patriarch. Following the sack of Constantinople by Western crusaders in 1204, the manuscript was taken to an isolated Greek monastery in Palest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CRC Press
The CRC Press, LLC is an American publishing group that specializes in producing technical books. Many of their books relate to engineering, science and mathematics. Their scope also includes books on business, forensics and information technology. CRC Press is now a division of Taylor & Francis, itself a subsidiary of Informa. History The CRC Press was founded as the Chemical Rubber Company (CRC) in 1903 by brothers Arthur, Leo and Emanuel Friedman in Cleveland, Ohio, based on an earlier enterprise by Arthur, who had begun selling rubber laboratory aprons in 1900. The company gradually expanded to include sales of laboratory equipment to chemist A chemist (from Greek ''chēm(ía)'' alchemy; replacing ''chymist'' from Medieval Latin ''alchemist'') is a graduated scientist trained in the study of chemistry, or an officially enrolled student in the field. Chemists study the composition of ...s. In 1913 the CRC offered a short (116-page) manual called the ''Rubber Handboo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a ; (: frusta or frustums) is the portion of a polyhedron, solid (normally a pyramid (geometry), pyramid or a cone (geometry), cone) that lies between two parallel planes cutting the solid. In the case of a pyramid, the base faces are polygonal and the side faces are trapezoidal. A ''right frustum'' is a right pyramid or a right cone truncation (geometry), truncated perpendicularly to its axis; otherwise, it is an ''oblique frustum''. In a ''truncated cone'' or ''truncated pyramid'', the truncation plane is necessarily parallel to the cone's base, as in a frustum. If all its edges are forced to become of the same length, then a frustum becomes a ''Prism (geometry), prism'' (possibly oblique or/and with irregular bases). Elements, special cases, and related concepts A frustum's axis is that of the original cone or pyramid. A frustum is circular if it has circular bases; it is right if the axis is perpendicular to both bases, and oblique otherwise. The height of a f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Function
Although the function is not defined at zero, as becomes closer and closer to zero, becomes arbitrarily close to 1. In other words, the limit of as approaches zero, equals 1. In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input which may or may not be in the domain of the function. Formal definitions, first devised in the early 19th century, are given below. Informally, a function assigns an output to every input . We say that the function has a limit at an input , if gets closer and closer to as moves closer and closer to . More specifically, the output value can be made ''arbitrarily'' close to if the input to is taken ''sufficiently'' close to . On the other hand, if some inputs very close to are taken to outputs that stay a fixed distance apart, then we say the limit ''does not exist''. The notion of a limit has many applications in modern calc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Encyclopædia Britannica
The is a general knowledge, general-knowledge English-language encyclopaedia. It has been published by Encyclopædia Britannica, Inc. since 1768, although the company has changed ownership seven times. The 2010 version of the 15th edition, which spans 32 volumes and 32,640 pages, was the last printed edition. Since 2016, it has been published exclusively as an online encyclopedia, online encyclopaedia. Printed for 244 years, the ''Britannica'' was the longest-running in-print encyclopaedia in the English language. It was first published between 1768 and 1771 in Edinburgh, Scotland, in three volumes. The encyclopaedia grew in size; the second edition was 10 volumes, and by its fourth edition (1801–1810), it had expanded to 20 volumes. Its rising stature as a scholarly work helped recruit eminent contributors, and the 9th (1875–1889) and Encyclopædia Britannica Eleventh Edition, 11th editions (1911) are landmark encyclopaedias for scholarship and literary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |