|
Newton's Minimal Resistance Problem
Newton's minimal resistance problem is a problem of finding a solid of revolution which experiences a minimum resistance when it moves through a homogeneous fluid with constant velocity in the direction of the axis of revolution, named after Isaac Newton, who studied the problem in 1685 and published it in 1687 in his Principia Mathematica. This is the first example of a problem solved in what is now called the calculus of variations The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions t ..., appearing a decade before the brachistochrone problem. Newton published the solution in Principia Mathematica without his derivation and David Gregory was the first person who approached Newton and persuaded him to write an analysis for him. Then the derivation was shared with his students and peers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a solid figure obtained by rotating a plane figure around some straight line (the '' axis of revolution'') that lies on the same plane. The surface created by this revolution and which bounds the solid is the surface of revolution. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area ( Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, accoun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophiæ Naturalis Principia Mathematica
( English: ''Mathematical Principles of Natural Philosophy'') often referred to as simply the (), is a book by Isaac Newton that expounds Newton's laws of motion and his law of universal gravitation. The ''Principia'' is written in Latin and comprises three volumes, and was first published on 5 July 1687. The is considered one of the most important works in the history of science. The French mathematical physicist Alexis Clairaut assessed it in 1747: "The famous book of ''Mathematical Principles of Natural Philosophy'' marked the epoch of a great revolution in physics. The method followed by its illustrious author Sir Newton ... spread the light of mathematics on a science which up to then had remained in the darkness of conjectures and hypotheses." A more recent assessment has been that while acceptance of Newton's laws was not immediate, by the end of the century after publication in 1687, "no one could deny that" (out of the ) "a science had emerged that, at least in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus Of Variations
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as '' geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brachistochrone Curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: Thomson Brooks/Cole, 2012. 640. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Gregory (mathematician)
David Gregory (originally spelt Gregorie) Fellow of the Royal Society, FRS (3 June 1659 – 10 October 1708) was a Scottish mathematician and astronomer. He was professor of mathematics at the University of Edinburgh, and later Savilian Professor of Astronomy at the University of Oxford, and a proponent of Isaac Newton's ''Philosophiæ Naturalis Principia Mathematica, Principia''. Biography The fourth of the fifteen children of David Gregory (physician), David Gregorie, a doctor from Kinnairdy, Banffshire, and Jean Walker of Orchiston, David was born in Upper Kirkgate, Aberdeen. The nephew of astronomer and mathematician James Gregory (astronomer and mathematician), James Gregory, David, like his influential uncle before him, studied at Aberdeen Grammar School and Marischal College (University of Aberdeen), from 1671 to 1675. The Gregorys were Jacobitism, Jacobites and left Scotland to escape religious discrimination. Young David visited several countries on the continent, incl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of California Press
The University of California Press, otherwise known as UC Press, is a publishing house associated with the University of California that engages in academic publishing. It was founded in 1893 to publish scholarly and scientific works by faculty of the University of California, established 25 years earlier in 1868, and has been officially headquartered at the university's flagship campus in Berkeley, California, since its inception. As the non-profit publishing arm of the University of California system, the UC Press is fully subsidized by the university and the State of California. A third of its authors are faculty members of the university. The press publishes over 250 new books and almost four dozen multi-issue journals annually, in the humanities, social sciences, and natural sciences, and maintains approximately 4,000 book titles in print. It is also the digital publisher of Collabra and Luminos open access (OA) initiatives. The University of California Press publishes i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Spo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypersonic Flow
In aerodynamics, a hypersonic speed is one that exceeds 5 times the speed of sound, often stated as starting at speeds of Mach 5 and above. The precise Mach number at which a craft can be said to be flying at hypersonic speed varies, since individual physical changes in the airflow (like molecular dissociation and ionization) occur at different speeds; these effects collectively become important around Mach 5-10. The hypersonic regime can also be alternatively defined as speeds where specific heat capacity changes with the temperature of the flow as kinetic energy of the moving object is converted into heat. Characteristics of flow While the definition of hypersonic flow can be quite vague and is generally debatable (especially due to the absence of discontinuity between supersonic and hypersonic flows), a hypersonic flow may be characterized by certain physical phenomena that can no longer be analytically discounted as in supersonic flow. The peculiarity in hypersonic flows ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
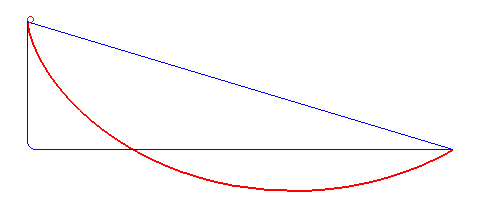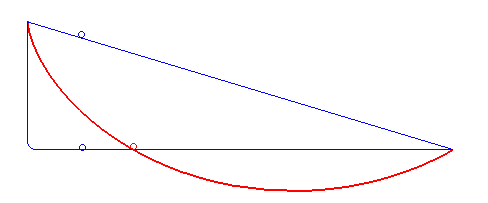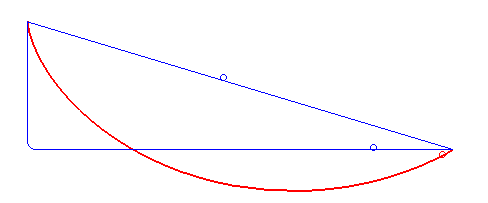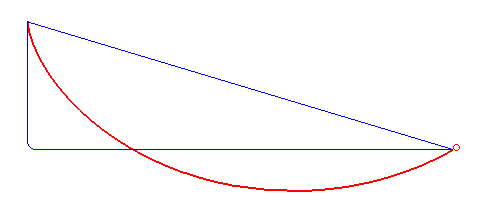
Min Resistance Problem Diagram
Min or MIN may refer to: Places * Fujian, also called Mǐn, a province of China ** Min Kingdom (909–945), a state in Fujian * Min County, a county of Dingxi, Gansu province, China * Min River (Fujian) * Min River (Sichuan) * Mineola (Amtrak station), station code MIN People Personal names * Min (Korean name), Korean surname and given names * Min (surname) (闵/閔), a Chinese surname Individuals with the name * Min (Vietnamese singer) (born 1988) * Min (Korean singer) (born 1991), South Korean singer, songwriter and actress Lee Min-young * Min (treasurer), ancient Egyptian official * Min, Marquis of Jin (died 678 BC), Chinese monarch * Empress Myeongseong (1851–1895), informally Queen Min, empress of Joseon * Menes or Min (a spelling variant no longer accepted), an early Egyptian pharaoh * Min Hogg (born 1939), British journalist and magazine editor * Min, a character from ''Barney & Friends'' played by Pia Hamilton from 1992 to 1995 * Min Hael Cassidy, a character from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Lagrange Equation
In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered in the 1750s by Swiss mathematician Leonhard Euler and Italian mathematician Joseph-Louis Lagrange. Because a differentiable functional is stationary at its local extrema, the Euler–Lagrange equation is useful for solving optimization problems in which, given some functional, one seeks the function minimizing or maximizing it. This is analogous to Fermat's theorem in calculus, stating that at any point where a differentiable function attains a local extremum its derivative is zero. In Lagrangian mechanics, according to Hamilton's principle of stationary action, the evolution of a physical system is described by the solutions to the Euler equation for the action of the system. In this context Euler equations are usually called Lagra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frustum
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal, the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise it is an oblique frustum. If all its edges are forced to become of the same length, then a frustum becomes a prism (possibly oblique or/and with irregular bases). In computer graphics, the viewing frustum is the three-dimensional region which is visible on the screen. It is formed by a clipped pyramid; in particular, '' frustum culling'' is a method of hidden surface determination. In the aerospace industry, a frustum is the fairing between two stages of a multistage rocket (such as the Saturn V), which is shaped like a truncated cone. Elements, special cases, and related concepts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |





_Mach_7_computational_fluid_dynamic_(CFD).jpg)