|
Negative Temperature
Certain system (thermodynamics), systems can achieve negative thermodynamic temperature; that is, their Thermodynamic temperature, temperature can be expressed as a negative number, negative quantity on the Kelvin or Rankine scale, Rankine scales. This should be distinguished from temperatures expressed as negative numbers on non-thermodynamic Celsius scale, Celsius or Fahrenheit scales, which are nevertheless higher than absolute zero. A system with a truly negative temperature on the Kelvin scale is ''hotter'' than any system with a positive temperature. If a negative-temperature system and a positive-temperature system come in contact, heat will flow from the negative- to the positive-temperature system. A standard example of such a system is population inversion in laser physics. Thermodynamic systems with unbounded phase space cannot achieve negative temperatures: adding heat always increases their entropy. The possibility of a decrease in entropy as energy increases requir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-dimensional Point Vortex Gas
The two-dimensional point vortex gas is a discrete particle model used to study turbulence in two-dimensional ideal fluids. The two-dimensional guiding-center plasma is a completely equivalent model used in plasma physics. General setup The model is a Hamiltonian system of ''N'' points in the two-dimensional plane executing the motion :k_i\frac = \frac,\qquad k_i\frac = -\frac, (In the confined version of the problem, the logarithmic potential is modified.) Interpretations In the point-vortex gas interpretation, the particles represent either point vortices in a two-dimensional fluid, or parallel line vortices in a three-dimensional fluid. The constant ''k''''i'' is the circulation of the fluid around the ''i''th vortex. The Hamiltonian ''H'' is the interaction term of the fluid's integrated kinetic energy; it may be either positive or negative. The equations of motion simply reflect the drift of each vortex's position in the velocity field of the other vortices. In the guidin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Entropy
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of large ensembles of microscopic states that constitute thermodynamic systems. Boltzmann's principle Ludwig Boltzmann defined entropy as a measure of the number of possible microscopic states (''microstates'') of a system in thermodynamic equilibrium, consistent with its macroscopic thermodynamic properties, which constitute the ''macrostate'' of the system. A useful illustration is the example ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Function
In the thermodynamics of equilibrium, a state function, function of state, or point function for a thermodynamic system is a mathematical function relating several state variables or state quantities (that describe equilibrium states of a system) that depend only on the current equilibrium thermodynamic state of the system (e.g. gas, liquid, solid, crystal, or emulsion), not the path which the system has taken to reach that state. A state function describes equilibrium states of a system, thus also describing the type of system. A state variable is typically a state function so the determination of other state variable values at an equilibrium state also determines the value of the state variable as the state function at that state. The ideal gas law is a good example. In this law, one state variable (e.g., pressure, volume, temperature, or the amount of substance in a gaseous equilibrium system) is a function of other state variables so is regarded as a state function. A stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
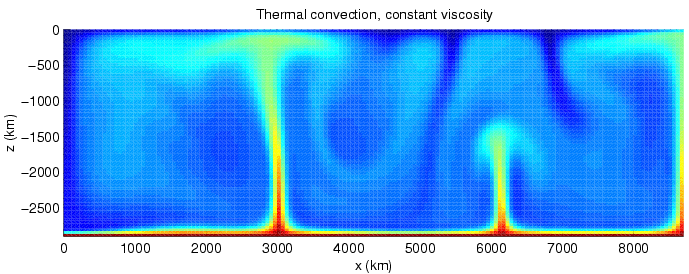
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Beta
In statistical thermodynamics, thermodynamic beta, also known as coldness, is the reciprocal of the thermodynamic temperature of a system:\beta = \frac (where is the temperature and is Boltzmann constant). Thermodynamic beta has units reciprocal to that of energy (in SI units, reciprocal joules, beta= \textrm^). In non-thermal units, it can also be measured in byte per joule, or more conveniently, gigabyte per nanojoule; 1 K−1 is equivalent to about 13,062 gigabytes per nanojoule; at room temperature: = 300K, β ≈ ≈ ≈ . The conversion factor is 1 GB/nJ = 8\ln2\times 10^ J−1. Description Thermodynamic beta is essentially the connection between the information theory and statistical mechanics interpretation of a physical system through its entropy and the thermodynamics associated with its energy. It expresses the response of entropy to an increase in energy. If a small amount of energy is added to the system, then ''β'' describes the amount the system will ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, ''i.e.'', the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. Without a thermodynamic process, the internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics. The notion has been introduced to describe the systems characterized by temperature variations, te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann's Entropy Formula
In statistical mechanics, Boltzmann's entropy formula (also known as the Boltzmann–Planck equation, not to be confused with the more general Boltzmann equation, which is a partial differential equation) is a probability equation relating the entropy S, also written as S_\mathrm, of an ideal gas to the multiplicity (commonly denoted as \Omega or W), the number of real microstates corresponding to the gas's macrostate: where k_\mathrm B is the Boltzmann constant (also written as simply k) and equal to 1.380649 × 10−23 J/K, and \ln is the natural logarithm function (or log base e, as in the image above). In short, the Boltzmann formula shows the relationship between entropy and the number of ways the atoms or molecules of a certain kind of thermodynamic system can be arranged. History The equation was originally formulated by Ludwig Boltzmann between 1872 and 1875, but later put into its current form by Max Planck in about 1900. To quote Planck, "the logarithmic c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature, also known as absolute temperature, is a physical quantity which measures temperature starting from absolute zero, the point at which particles have minimal thermal motion. Thermodynamic temperature is typically expressed using the Kelvin scale, where the unit of measurement is the ''kelvin'' (unit symbol: K). The Kelvin scale uses the same degree interval as the Celsius scale but is offset so that 0 K corresponds to absolute zero. For comparison, a temperature of 295 K corresponds to 21.85 °C and 71.33 °F. Another absolute scale of temperature is the Rankine scale, which is based on the Fahrenheit degree interval. Historically, thermodynamic temperature was defined by Lord Kelvin in terms of a macroscopic relation between Work (thermodynamics), thermodynamic work and Heat, heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |