|
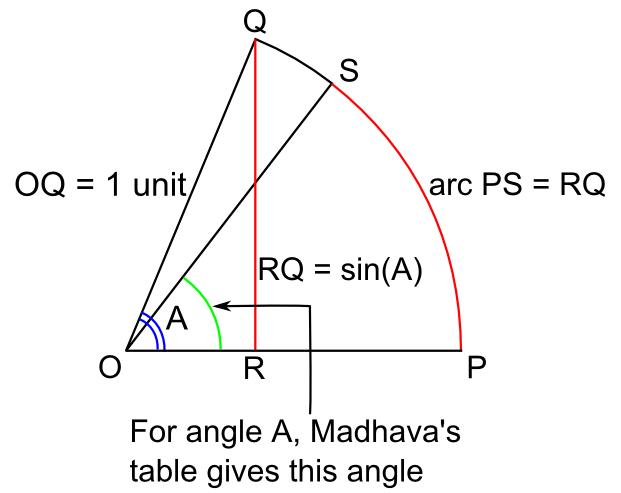
Mādhava's Sine Table
Madhava's sine table is the table of trigonometric sines constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama (c. 1340 – c. 1425). The table lists the jya-s or Rsines of the twenty-four angles from 3.75 ° to 90° in steps of 3.75° (1/24 of a right angle, 90°). Rsine is just the sine multiplied by a selected radius and given as an integer. In this table, as in Aryabhata's earlier table, ''R'' is taken as 21600 ÷ 2 ≈ 3437.75. The table is encoded in the letters of the Sanskrit alphabet using the Katapayadi system, giving entries the appearance of the verses of a poem. Madhava's original work containing the table has not been found. The table is reproduced in the ''Aryabhatiyabhashya'' of Nilakantha Somayaji''The Aryabhatiam of Aryabhattacharya with the Bhashya of Nilakantha Somasutvan, Part 1 - Gaṇitapāda,'' Edited by K. Sambasiva Sastri, Trivandrum Sanskrit Series No.101. p. 55. https://archive.org/details/Triva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Table (information)
A table is an arrangement of information or data, typically in rows and columns, or possibly in a more complex structure. Tables are widely used in communication, research, and data analysis. Tables appear in print media, handwritten notes, computer software, architectural ornamentation, traffic signs, and many other places. The precise conventions and terminology for describing tables vary depending on the context. Further, tables differ significantly in variety, structure, flexibility, notation, representation and use. Information or data conveyed in table form is said to be in tabular format (adjective). In books and technical articles, tables are typically presented apart from the main text in numbered and captioned floating blocks. Basic description A table consists of an ordered arrangement of rows and columns. This is a simplified description of the most basic kind of table. Certain considerations follow from this simplified description: * the term row has several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karanapaddhati
Karanapaddhati is an astronomical treatise in Sanskrit attributed to Puthumana Somayaji, an astronomer-mathematician of the Kerala school of astronomy and mathematics. The period of composition of the work is uncertain. C.M. Whish, a civil servant of the East India Company, brought this work to the attention of European scholars for the first time in a paper published in 1834. The book is divided into ten chapters and is in the form of verses in Sanskrit. The sixth chapter contains series expansions for the value of the mathematical constant π, and expansions for the trigonometric sine, cosine and inverse tangent functions. Author and date of Karanapaddhati Nothing definite is known about the author of Karanapaddhati. The last verse of the tenth chapter of Karanapaddhati describes the author as a Brahamin residing in a village named Sivapura. Sivapura is an area surrounding the present day Thrissur in Kerala, India. The period in which Somayaji lived is also uncertain. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Madhava Series
In mathematics, a Madhava series is one of the three Taylor series expansions for the sine, cosine, and arctangent function (mathematics), functions discovered in 14th or 15th century in Kerala, India by the mathematician and astronomer Madhava of Sangamagrama (c. 1350 – c. 1425) or his followers in the Kerala school of astronomy and mathematics. Using modern notation, these series are: :\begin \sin \theta &= \theta - \frac + \frac - \frac + \cdots &&= \sum_^\infty \frac\theta^, \\[10mu] \cos \theta &= 1 - \frac + \frac - \frac + \cdots &&= \sum_^\infty \frac\theta^, \\[10mu] \arctan x &= x - \frac + \frac - \frac + \cdots &&= \sum_^\infty \fracx^ \quad \text , x, \leq 1. \end All three series were later independently discovered in 17th century Europe. The series for sine and cosine were rediscovered by Isaac Newton in 1669, and the series for arctangent was rediscovered by James Gregory (mathematician), James Gregory in 1671 and Gottfried Wilhelm Leibniz, Gottfried ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine And Cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that angle to the length of the longest side of the triangle (the hypotenuse), and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle \theta, the sine and cosine functions are denoted as \sin(\theta) and \cos(\theta). The definitions of sine and cosine have been extended to any real value in terms of the lengths of certain line segments in a unit circle. More modern definitions express the sine and cosine as infinite series, or as the solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers. The sine and cosine functions are commonly used to model periodic phenomena such as sound and light waves, the position a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yuktibhāṣā
''Yuktibhāṣā'' (), also known as Gaṇita-yukti-bhāṣā and ( English: ''Compendium of Astronomical Rationale''), is a major treatise on mathematics and astronomy, written by the Indian astronomer Jyesthadeva of the Kerala school of mathematics around 1530. The treatise, written in Malayalam, is a consolidation of the discoveries by Madhava of Sangamagrama, Nilakantha Somayaji, Parameshvara, Jyeshtadeva, Achyuta Pisharati, and other astronomer-mathematicians of the Kerala school. It also exists in a Sanskrit version, with unclear author and date, composed as a rough translation of the Malayalam original. The work contains proofs and derivations of the theorems that it presents. Modern historians used to assert, based on the works of Indian mathematics that first became available, that early Indian scholars in astronomy and computation lacked in proofs, but demonstrates otherwise. Some of its important topics include the infinite series expansions of functions; pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tantrasangraha
Tantrasamgraha, or Tantrasangraha, (literally, ''A Compilation of the System'') is an important astronomical treatise written by Nilakantha Somayaji, an astronomer/mathematician belonging to the Kerala school of astronomy and mathematics. The treatise was completed in 1501 CE. It consists of 432 verses in Sanskrit divided into eight chapters. Tantrasamgraha had spawned a few commentaries: ''Tantrasamgraha-vyakhya'' of anonymous authorship and ''Yuktibhāṣā'' authored by Jyeshtadeva in about 1550 CE. Tantrasangraha, together with its commentaries, bring forth the depths of the mathematical accomplishments the Kerala school of astronomy and mathematics, in particular the achievements of the remarkable mathematician of the school Sangamagrama Madhava. In his ''Tantrasangraha'', Nilakantha revised Aryabhata's model for the planets Mercury and Venus. According to George G Joseph his equation of the centre for these planets remained the most accurate until the time of Johannes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arcsecond
A minute of arc, arcminute (abbreviated as arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of a degree. Since one degree is of a turn, or complete rotation, one arcminute is of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth's circumference is very near . A minute of arc is of a radian. A second of arc, arcsecond (abbreviated as arcsec), or arc second, denoted by the symbol , is a unit of angular measurement equal to of a minute of arc, of a degree, of a turn, and (about ) of a radian. These units originated in Babylonian astronomy as sexagesimal (base 60) subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship. To express even smaller angles, standard SI prefixes can be employed; the milliarcse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |