|
Möller–Trumbore Intersection Algorithm
The Möller–Trumbore ray-triangle intersection algorithm, named after its inventors Tomas Möller and Ben Trumbore, is a fast method for calculating the intersection of a ray and a triangle in three dimensions without needing precomputation of the plane equation of the plane containing the triangle. Among other uses, it can be used in computer graphics to implement ray tracing computations involving triangle meshes. Calculation Definitions The ray is defined by an origin point O and a direction vector \vec. Every point on the ray can be expressed by \vec(t) = O + t\vec, where the parameter t ranges from zero to infinity. The triangle is defined by three vertices, named v_1, v_2, v_3. The plane that the triangle is on, which is needed to calculate the ray-triangle intersection, is defined by a point on the plane, such as v_1, and a vector that is orthogonal to every point on that plane, such as the cross product between the vector from v_1 to v_2 and the vector from v_1 to v_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection (Euclidean Geometry)
In geometry, an intersection is a point, line, or curve common to two or more objects (such as lines, curves, planes, and surfaces). The simplest case in Euclidean geometry is the line–line intersection between two distinct lines, which either is one point or does not exist (if the lines are parallel). Other types of geometric intersection include: * Line–plane intersection * Line–sphere intersection * Intersection of a polyhedron with a line * Line segment intersection * Intersection curve Determination of the intersection of flats – linear geometric objects embedded in a higher-dimensional space – is a simple task of linear algebra, namely the solution of a system of linear equations. In general the determination of an intersection leads to non-linear equations, which can be solved numerically, for example using Newton iteration. Intersection problems between a line and a conic section (circle, ellipse, parabola, etc.) or a quadric (sphere, cylinder, hyperboloid, et ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
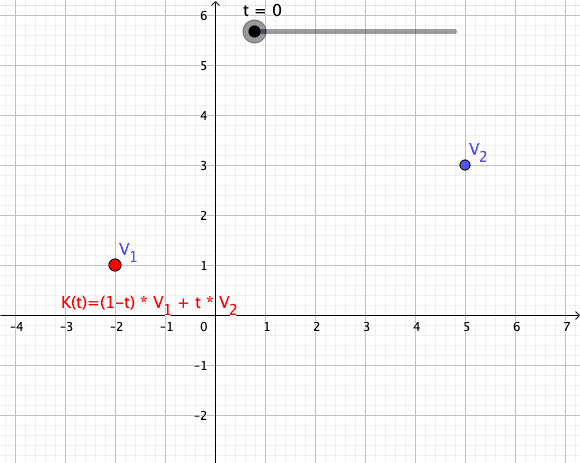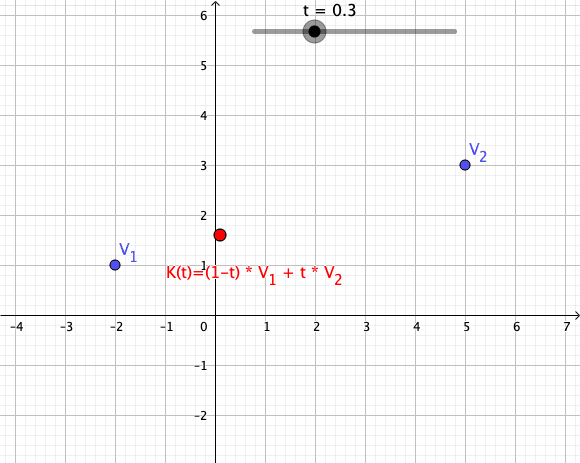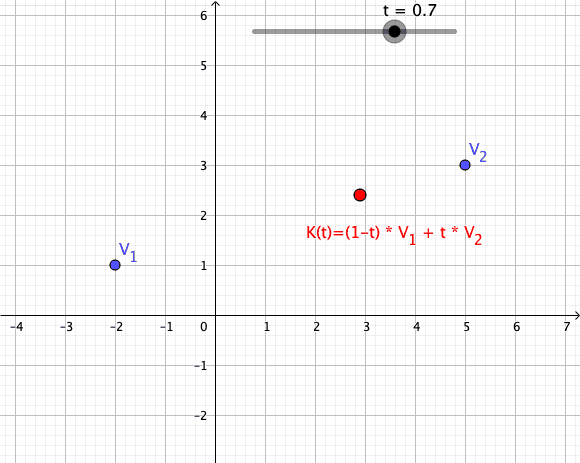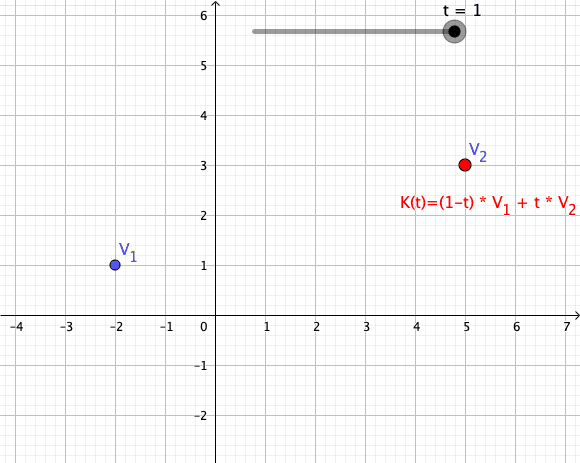
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is id ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Badouel Intersection Algorithm
The Badouel ray-triangle intersection algorithm, named after its inventor Didier Badouel, is a fast method for calculating the intersection of a ray and a triangle in three dimensions without needing precomputation of the plane equation of the plane Plane(s) most often refers to: * Aero- or airplane, a powered, fixed-wing aircraft * Plane (geometry), a flat, 2-dimensional surface Plane or planes may also refer to: Biology * Plane (tree) or ''Platanus'', wetland native plant * ''Planes'' ... containing the triangle. External links Ray-Polygon IntersectionAn Efficient Ray-Polygon Intersection by Didier Badouel from Graphics Gems I Computational geometry {{Algorithm-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Java 3D
Java 3D is a scene graph-based 3D application programming interface (API) for the Java platform. It runs on top of either OpenGL or Direct3D until version 1.6.0, which runs on top of Java OpenGL (JOGL). Since version 1.2, Java 3D has been developed under the Java Community Process. A Java 3D scene graph is a directed acyclic graph (DAG). Compared to other solutions, Java 3D is not only a wrapper around these graphics APIs, but an interface that encapsulates the graphics programming using a true object-oriented approach. Here a scene is constructed using a scene graph that is a representation of the objects that have to be shown. This scene graph is structured as a tree containing several elements that are necessary to display the objects. Additionally, Java 3D offers extensive spatialized sound support. Java 3D and its documentation are available for download separately. They are not part of the Java Development Kit (JDK). History Intel, Silicon Graphics, Apple, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Java (programming Language)
Java is a high-level, class-based, object-oriented programming language that is designed to have as few implementation dependencies as possible. It is a general-purpose programming language intended to let programmers ''write once, run anywhere'' ( WORA), meaning that compiled Java code can run on all platforms that support Java without the need to recompile. Java applications are typically compiled to bytecode that can run on any Java virtual machine (JVM) regardless of the underlying computer architecture. The syntax of Java is similar to C and C++, but has fewer low-level facilities than either of them. The Java runtime provides dynamic capabilities (such as reflection and runtime code modification) that are typically not available in traditional compiled languages. , Java was one of the most popular programming languages in use according to GitHub, particularly for client–server web applications, with a reported 9 million developers. Java was originally de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rust (programming Language)
Rust is a multi-paradigm, general-purpose programming language. Rust emphasizes performance, type safety, and concurrency. Rust enforces memory safety—that is, that all references point to valid memory—without requiring the use of a garbage collector or reference counting present in other memory-safe languages. To simultaneously enforce memory safety and prevent concurrent data races, Rust's "borrow checker" tracks the object lifetime of all references in a program during compilation. Rust is popular for systems programming but also offers high-level features including some functional programming constructs. Software developer Graydon Hoare created Rust as a personal project while working at Mozilla Research in 2006. Mozilla officially sponsored the project in 2009. Since the first stable release in May 2015, Rust has been adopted by companies including Amazon, Discord, Dropbox, Facebook ( Meta), Google (Alphabet), and Microsoft. Rust has been noted for its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramer's Rule
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-sides of the equations. It is named after Gabriel Cramer (1704–1752), who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748 (and possibly knew of it as early as 1729). Cramer's rule implemented in a naive way is computationally inefficient for systems of more than two or three equations. In the case of equations in unknowns, it requires computation of determinants, while Gaussian elimination produces the result with the same computational complexity as the computation of a single determinant. Cramer's rule can also be nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invertible
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers. Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that is a right inverse of . (An identity element is an element such that and for all and for which the left-hand sides are defined.) When the operation is associative, if an element has both a left inverse and a right inverse, then these two inverses are equal and unique; they are called the ''inverse element'' or simply the ''inverse''. Often an adjective is added for specifying the operation, such as in additive inverse, multiplicative inverse, and functional inverse. In this case (associative operation), an invertible element is an element that has an inverse. Inverses are commonly used in groupswhere every element is invertible, and ringswhere invertible elements are also called units. They are also commonly used for operation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barycentric Coordinate System
In geometry, a barycentric coordinate system is a coordinate system in which the location of a point is specified by reference to a simplex (a triangle for points in a plane (mathematics), plane, a tetrahedron for points in three-dimensional space, etc.). The barycentric coordinates of a point can be interpreted as masses placed at the vertices of the simplex, such that the point is the center of mass (or ''barycenter'') of these masses. These masses can be zero or negative; they are all positive if and only if the point is inside the simplex. Every point has barycentric coordinates, and their sum is not zero. Two tuples of barycentric coordinates specify the same point if and only if they are proportional; that is to say, if one tuple can be obtained by multiplying the elements of the other tuple by the same non-zero number. Therefore, barycentric coordinates are either considered to be defined up to multiplication by a nonzero constant, or normalized for summing to unity. Bar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray (geometry)
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry). In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Mesh
In computer graphics, a triangle mesh is a type of polygon mesh. It comprises a set of triangles (typically in three dimensions) that are connected by their common edges or vertices. Many graphics software packages and hardware devices can operate more efficiently on triangles that are grouped into meshes than on a similar number of triangles that are presented individually. This is typically because computer graphics do operations on the vertices at the corners of triangles. With individual triangles, the system has to operate on three vertices for every triangle. In a large mesh, there could be eight or more triangles meeting at a single vertex - by processing those vertices just once, it is possible to do a fraction of the work and achieve an identical effect. In many computer graphics applications it is necessary to manage a mesh of triangles. The mesh components are vertices, edges, and triangles. An application might require knowledge of the various connections betw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |