|
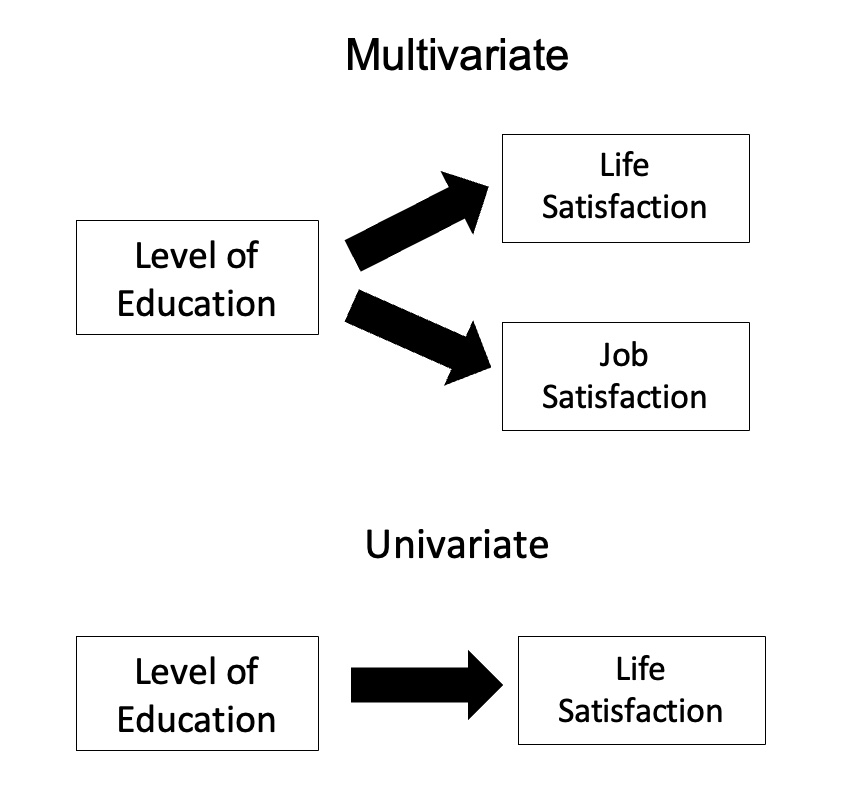
Multivariate Analysis Of Variance
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate random variable, multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately. Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers. Model Assume n q-dimensional observations, where the i’th observation y_i is assigned to the group g(i)\in \ and is distributed around the group center \mu^\in \mathbb R^q with Multivariate normal distribution, multivariate Ga ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Univariate Vs
In mathematics, a univariate object is an expression, equation, function or polynomial involving only one variable. Objects involving more than one variable are '' multivariate''. In some cases the distinction between the univariate and multivariate cases is fundamental; for example, the fundamental theorem of algebra and Euclid's algorithm for polynomials are fundamental properties of univariate polynomials that cannot be generalized to multivariate polynomials. In statistics, a univariate distribution characterizes one variable, although it can be applied in other ways as well. For example, univariate data are composed of a single scalar component. In time series analysis, the whole time series is the "variable": a univariate time series is the series of values over time of a single quantity. Correspondingly, a "multivariate time series" characterizes the changing values over time of several quantities. In some cases, the terminology is ambiguous, since the values within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilks' Lambda Distribution
In statistics, Wilks' lambda distribution (named for Samuel S. Wilks), is a probability distribution used in multivariate hypothesis testing, especially with regard to the likelihood-ratio test and multivariate analysis of variance (MANOVA). Definitions Wilks' lambda distribution is defined from two independent Wishart distributed variables as the ratio distribution of their determinant In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...s, given :\mathbf \sim W_p(\Sigma, m) \qquad \mathbf \sim W_p(\Sigma, n) independent and with m \ge p :\lambda = \frac = \frac \sim \Lambda(p,m,n) where ''p'' is the number of dimensions. In the context of likelihood-ratio tests ''m'' is typically the error degrees of freedom, and ''n'' is the hypothesis degrees of freedom, so that n+m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Correlation Analysis
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X''''n'') and ''Y'' = (''Y''1, ..., ''Y''''m'') of random variables, and there are correlations among the variables, then canonical-correlation analysis will find linear combinations of ''X'' and ''Y'' that have a maximum correlation with each other. T. R. Knapp notes that "virtually all of the commonly encountered parametric tests of significance can be treated as special cases of canonical-correlation analysis, which is the general procedure for investigating the relationships between two sets of variables." The method was first introduced by Harold Hotelling in 1936, although in the context of angles between flats the mathematical concept was published by Camille Jordan in 1875. CCA is now a cornerstone of multivariate statistics a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Function Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later statistical classification, classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical variable, categorical independent variables and a continuous variable, continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Permutational Analysis Of Variance
Permutational multivariate analysis of variance (PERMANOVA), is a non-parametric multivariate statistical permutation test. PERMANOVA is used to compare groups of objects and test the null hypothesis that the centroids and dispersion of the groups as defined by measure space are equivalent for all groups. A rejection of the null hypothesis means that either the centroid and/or the spread of the objects is different between the groups. Hence the test is based on the prior calculation of the distance between any two objects included in the experiment. PERMANOVA shares some resemblance to ANOVA where they both measure the sum-of-squares within and between groups, and make use of F test to compare within-group to between-group variance. However, while ANOVA bases the significance of the result on assumption of normality, PERMANOVA draws tests for significance by comparing the actual F test result to that gained from random permutations of the objects between the groups. Moreover, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outcome Variables
{{disambig ...
Outcome may refer to: * Outcome (probability), the result of an experiment in probability theory * Outcome (game theory), the result of players' decisions in game theory * ''The Outcome'', a 2005 Spanish film * An outcome measure (or endpoint) in a clinical trial *The National Outcomes adopted as targets by the Scottish Government See also * Outcome-based education * Outcomes theory Outcomes theory provides the conceptual basis for thinking about, and working with outcomes systems of any type. An outcomes system is any system that: identifies; prioritizes; measures; attributes; or hold parties to account for outcomes of any ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Linear Model
The general linear model or general multivariate regression model is a compact way of simultaneously writing several multiple linear regression models. In that sense it is not a separate statistical linear model. The various multiple linear regression models may be compactly written as : \mathbf = \mathbf\mathbf + \mathbf, where Y is a Matrix (mathematics), matrix with series of multivariate measurements (each column being a set of measurements on one of the dependent variables), X is a matrix of observations on independent variables that might be a design matrix (each column being a set of observations on one of the independent variables), B is a matrix containing parameters that are usually to be estimated and U is a matrix containing Errors and residuals in statistics, errors (noise). The errors are usually assumed to be uncorrelated across measurements, and follow a multivariate normal distribution. If the errors do not follow a multivariate normal distribution, generalized li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hotelling's T-square
In statistics, particularly in hypothesis testing, the Hotelling's ''T''-squared distribution (''T''2), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the ''F''-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's ''t''-distribution. The Hotelling's ''t''-squared statistic (''t''2) is a generalization of Student's ''t''-statistic that is used in multivariate hypothesis testing. Motivation The distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a ''t''-test. The distribution is named for Harold Hotelling, who developed it as a generalization of Student's ''t''-distribution. Definition If the vector d is Gaussian multivariate-distributed with zero mean and u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Multivariate Analysis
The ''Journal of Multivariate Analysis'' is a monthly peer-reviewed scientific journal that covers applications and research in the field of multivariate statistical analysis. The journal's scope includes theoretical results as well as applications of new theoretical methods in the field. Some of the research areas covered include copula modeling, functional data analysis, graphical modeling, high-dimensional data analysis, image analysis, multivariate extreme-value theory, sparse modeling, and spatial statistics. According to the ''Journal Citation Reports'', the journal has a 2017 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 1.009. See also * List of statistics journals References External links * Statistics journals Monthly journals Engli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roy's Greatest Root
Roy's is an upscale American restaurant that specializes in Hawaiian and Japanese fusion cuisine, with a focus on sushi, seafood and steak. The chain was founded by James Beard Foundation Award Winner Roy Yamaguchi in 1988 in Honolulu, Hawaii. The concept was well received among critics upon inception. The concept has grown to include 21 Roy's restaurants in the continental United States, six in Hawaii, one in Japan and one in Guam. Roy's is known best for its eclectic blend of Hawaiian, Japanese, and Classic French cuisine created by founder Roy Yamaguchi who was born in Tokyo, Japan, and spent his childhood visiting his grandparents who owned a tavern in Wailuku, Maui. Yamaguchi then graduated from the Culinary Institute of America where he received his formal culinary training and credits these factors to inspiring his unique culinary vision that is brought to life at Roy's. Twenty mainland locations were owned and operated by Bloomin' Brands, Inc., until December 2014 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |