|
Mersenne's Laws
Mersenne's laws are laws describing the frequency of oscillation of a stretched string or monochord, useful in musical tuning and musical instrument construction. Overview The equation was first proposed by French mathematician and music theorist Marin Mersenne in his 1636 work '' Harmonie universelle''.Mersenne, Marin (1636)''Harmonie universelle'' Cited in, '' Wolfram.com''. Mersenne's laws govern the construction and operation of string instruments, such as pianos and harps, which must accommodate the total tension force required to keep the strings at the proper pitch. Lower strings are thicker, thus having a greater mass per length. They typically have lower tension. Guitars are a familiar exception to this: string tensions are similar, for playability, so lower string pitch is largely achieved with increased mass per length. Higher-pitched strings typically are thinner, have higher tension, and may be shorter. "This result does not differ substantially from Galileo's, yet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a polymath. He was born in the city of Pisa, then part of the Duchy of Florence. Galileo has been called the father of observational astronomy, modern-era classical physics, the scientific method, and modern science. Galileo studied speed and velocity, gravity and free fall, the principle of relativity, inertia, projectile motion and also worked in applied science and technology, describing the properties of the pendulum and "hydrostatic balances". He was one of the earliest Renaissance developers of the thermoscope and the inventor of various sector (instrument), military compasses. With an improved telescope he built, he observed the stars of the Milky Way, the phases of Venus, the Galilean moons, four largest satellites of Jupiter, Saturn's r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
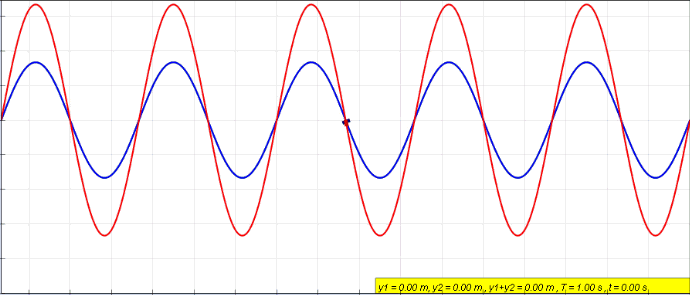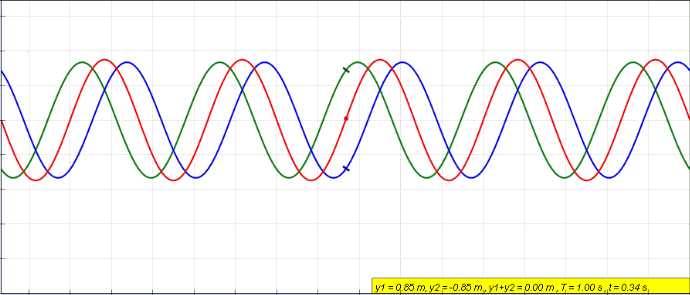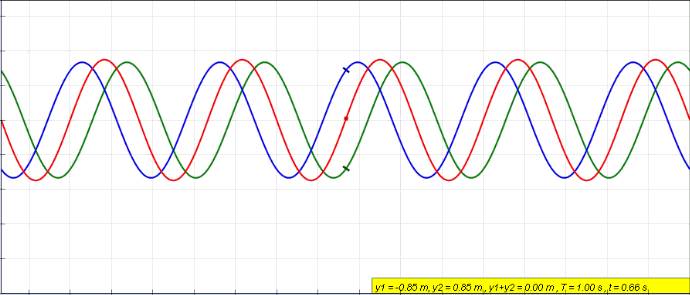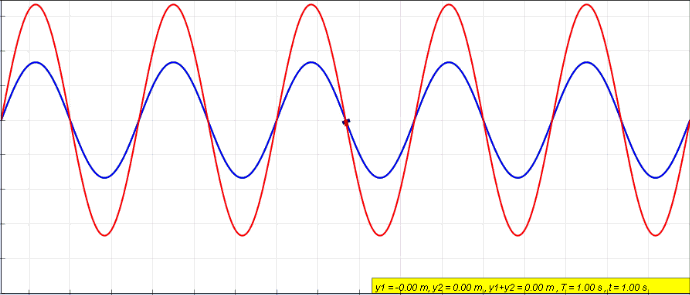
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called node (physics), nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first described scientifically by Michael Faraday in 1831. Faraday observed Faraday wave, standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overtone
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound. Using the model of Fourier analysis, the fundamental and the overtones together are called Harmonic series (music)#Partial, partials. Harmonics, or more precisely, harmonic partials, are partials whose frequencies are numerical integer multiples of the fundamental (including the fundamental, which is 1 times itself). These overlapping terms are variously used when discussing the acoustic behavior of musical instruments.Alexander John Ellis, A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long-string Instrument
The long-string instrument is a musical instrument in which the string is of such a length that the fundamental transverse wave is below what a person can hear as a tone (±20 Hz). If the tension and the length result in sounds with such a frequency, the tone becomes a beating frequency that ranges from a short reverb (approx 5–10 meters) to longer echo sounds (longer than 10 meters). Besides the beating frequency, the string also gives higher pitched natural overtones. Since the length is that long, this has an effect on the attack tone. The attack tone shoots through the string in a longitudinal wave and generates the typical science-fiction laser-gun sound as heard in ''Star Wars''. The sound is also similar to that occurring in upper electricity cables for trains. History A long string instrument was one of the techniques by which Mersenne tested Galileo's hypothesis, now known under Mersenne's name, by making string vibration speed visible and countable. For exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wind Instrument
A wind instrument is a musical instrument that contains some type of resonator (usually a tube) in which a column of air is set into vibration by the player blowing into (or over) a mouthpiece set at or near the end of the resonator. The pitch of the vibration is determined by the length of the tube and by manual modifications of the effective length of the vibrating column of air. In the case of some wind instruments, sound is produced by blowing through a reed; others require buzzing into a metal mouthpiece, while yet others require the player to blow into a hole at an edge, which splits the air column and creates the sound. Methods for obtaining different notes * Using different air columns for different tones, such as in the pan flute. These instruments can play several notes at once. * Changing the length of the vibrating air column by changing the length of the tube through engaging valves ''(see rotary valve, piston valve)'' which route the air through additional tubing, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship between given quantities. The plural of ''formula'' can be either ''formulas'' (from the most common English plural noun form) or, under the influence of scientific Latin, ''formulae'' (from the original Latin). In mathematics In mathematics, a formula generally refers to an equation or inequality relating one mathematical expression to another, with the most important ones being mathematical theorems. For example, determining the volume of a sphere requires a significant amount of integral calculus or its geometrical analogue, the method of exhaustion. However, having done this once in terms of some parameter (the radius for example), mathematicians have produced a formula to describe the volume of a sphere in terms of its radius: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4^2 = (-4)^2 = 16. Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'' or simply ''the square root'' (with a definite article, see below), which is denoted by \sqrt, where the symbol "\sqrt" is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case, 9. For non-negative , the principal square root can also be written in exponent notation, as x^. Every positive number has two square roots: \sqrt (which is positive) and -\sqrt (which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, from which all other units are derived. In the International System of Units (SI) system, the base unit for length is the metre. Length is commonly understood to mean the most extended size, dimension of a fixed object. However, this is not always the case and may depend on the position the object is in. Various terms for the length of a fixed object are used, and these include height, which is vertical length or vertical extent, width, breadth, and depth. ''Height'' is used when there is a base from which vertical measurements can be taken. ''Width'' and ''breadth'' usually refer to a shorter dimension than ''length''. ''Depth'' is used for the measure of a third dimension. Length is the measure of one spatial dimension, whereas area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proportionality (mathematics)
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio. The ratio is called ''coefficient of proportionality'' (or ''proportionality constant'') and its reciprocal is known as ''constant of normalization'' (or ''normalizing constant''). Two sequences are inversely proportional if corresponding elements have a constant product. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely related to ''linearity''. Direct proportionality Given an independent variable ''x'' and a dependent variable ''y'', ''y'' is directly proportional to ''x'' if there is a positive constant ''k'' such that: : y = kx The relation is oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a Periodic signal, periodic waveform. In music, the fundamental is the musical pitch (music), pitch of a note that is perceived as the lowest Harmonic series (music)#Partial, partial present. In terms of a superposition of Sine wave, sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency Zero-based numbering, counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc.) According to Benward and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |