|
Max Planck Institute For Mathematics In The Sciences
The Max Planck Institute for Mathematics in the Sciences (MPI MiS) in Leipzig is a research institute of the Max Planck Society. Founded on March 1, 1996, the institute works on projects which apply mathematics in various areas of natural sciences, in particular physics, biology, chemistry and material science. Research groups * Geometry and Complex Systems ( Jürgen Jost) * Pattern formation, energy landscapes and scaling laws ( Felix Otto) * Nonlinear algebra ( Bernd Sturmfels) * Applied analysis () * Geometry, groups and dynamics ( Anna Wienhard) * Discrete sets in geometry (Samantha Fairchild) * Geometry on surfaces (James Reed Farre) * Stochastic partial differential equations () * Mathematical software (Michael Joswig) * Mathematical machine learning (Guido Montúfar) * Learning and inference (Sayan Mukherjee) * Interdisciplinary frontiers of algebraic geometry (İrem Portakal) * Probability and variational methods in PDEs (Tobias Ried) * Mathematical structures in phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
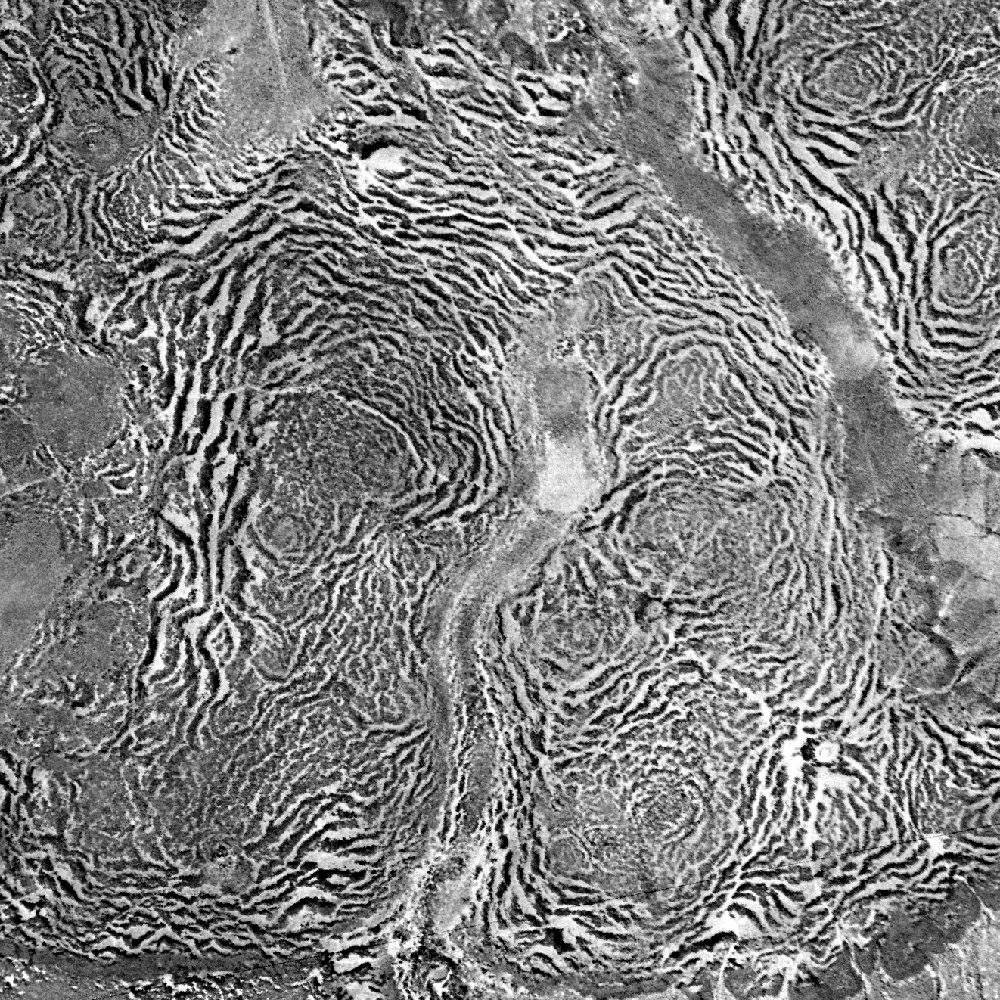
Pattern Formation
The science of pattern formation deals with the visible, (statistically) orderly outcomes of self-organization and the common principles behind similar patterns in nature. In developmental biology, pattern formation refers to the generation of complex organizations of cell fate determination, cell fates in space and time. The role of genes in pattern formation is an aspect of morphogenesis, the creation of diverse anatomy, anatomies from similar genes, now being explored in the science of evolutionary developmental biology or evo-devo. The mechanisms involved are well seen in the anterior-posterior patterning of embryos from the model organism ''Drosophila melanogaster'' (a fruit fly), one of the first organisms to have its morphogenesis studied, and in the eyespot (mimicry), eyespots of butterflies, whose development is a variant of the standard (fruit fly) mechanism. Patterns in nature Examples of pattern formation can be found in biology, physics, and science, and can readily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematics, mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and Industrial sector, industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the profession, professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of Mathematical analysis, applied analysis, most notably differential equations; approximation theory (broadly construed, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anna Wienhard
Anna Katharina Wienhard (born 1977)European Research Council Funds Heidelberg Mathematician Press Release, Ruprecht-Karls-Universität Heidelberg, February 5, 2014, retrieved 2015-01-18. is a German mathematician whose research concerns differential geometry, and especially the use of higher Teichmüller spaces to study the deformation theory of symmetry, symmetric geometric structures. She is a director at the Max Planck Institute for Mathematics in the Sciences.Anna Wienhard Scientific Members, Max-Planck-Gesellschaft, retrieved 2023-09-09 Education and career Wienhard did her undergraduate ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernd Sturmfels
Bernd Sturmfels (born March 28, 1962, in Kassel, West Germany) is a Professor of Mathematics and Computer Science at the University of California, Berkeley and is a director of the Max Planck Institute for Mathematics in the Sciences in Leipzig since 2017. Education and career He received his PhD in 1987 from the University of Washington and the Technische Universität Darmstadt. After two postdoctoral years at the Institute for Mathematics and its Applications in Minneapolis, Minnesota, and the Research Institute for Symbolic Computation in Linz, Austria, he taught at Cornell University, before joining University of California, Berkeley in 1995. His Ph.D. students include Melody Chan, Jesús A. De Loera, Mike Develin, Diane Maclagan, Rekha R. Thomas, Caroline Uhler, and Cynthia Vinzant. Contributions Bernd Sturmfels has made contributions to a variety of areas of mathematics, including algebraic geometry, commutative algebra, discrete geometry, Gröbner bases, toric varie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Algebra
Nonlinear algebra is the nonlinear analogue to linear algebra, generalizing notions of spaces and transformations coming from the linear setting. Algebraic geometry is one of the main areas of mathematical research supporting nonlinear algebra, while major components coming from computational mathematics support the development of the area into maturity. The topological setting for nonlinear algebra is typically the Zariski topology, where closed sets are the algebraic sets. Related areas in mathematics are tropical geometry, commutative algebra, and optimization. Algebraic geometry Nonlinear algebra is closely related to algebraic geometry, where the main objects of study include algebraic equations, algebraic varieties, and schemes. Computational nonlinear algebra Current methods in computational nonlinear algebra can be broadly broken into two domains: symbolic and numerical. Symbolic methods often rely on the computation of Gröbner bases and resultants. On the othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Otto (mathematician)
Felix Otto (born 19 May 1966) is a German mathematician. Biography He studied mathematics at the University of Bonn, finishing his PhD thesis in 1993 under the supervision of Stephan Luckhaus. After postdoctoral studies at the Courant Institute of Mathematical Sciences of New York University and at Carnegie Mellon University, in 1997 he became a professor at the University of California, Santa Barbara. From 1999 to 2010 he was professor for applied mathematics at the University of Bonn, and currently serves as one of the directors of the Max Planck Institute for Mathematics in the Sciences, Leipzig. Work Otto specialises in materials science, including work on the theory of partial differential equations. He is known for his work on the Otto–Villani theorem and the invention of the Otto calculus. Honours In 2006, he received the Gottfried Wilhelm Leibniz Prize of the Deutsche Forschungsgemeinschaft, which is the highest honour awarded in German research. In 2009, he was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scaling Law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy Landscape
Energy () is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat and light. Energy is a conserved quantity—the law of conservation of energy states that energy can be converted in form, but not created or destroyed. The unit of measurement for energy in the International System of Units (SI) is the joule (J). Forms of energy include the kinetic energy of a moving object, the potential energy stored by an object (for instance due to its position in a field), the elastic energy stored in a solid object, chemical energy associated with chemical reactions, the radiant energy carried by electromagnetic radiation, the internal energy contained within a thermodynamic system, and rest energy associated with an object's rest mass. These are not mutually exclusive. All living organisms constantly take in and release energy. The Earth's climate and ecosystems processes are driven pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jürgen Jost
Jürgen Jost (born 9 June 1956) is a German mathematician specializing in geometry. He has been a director of the Max Planck Institute for Mathematics in the Sciences in Leipzig since 1996. Life and work In 1975, he began studying mathematics, physics, economics and philosophy. In 1980 he received a Dr. rer. nat. from the University of Bonn under the supervision of . In 1984 he was at the University of Bonn for the habilitation. After his habilitation, he was at the Ruhr University Bochum, the chair of Mathematics X, Analysis. During this time he was the coordinator of the project "Stochastic Analysis and systems with infinitely many degrees of freedom" July 1987 to December 1996. For this work he received the 1993 Gottfried Wilhelm Leibniz Prize, awarded by the Deutsche Forschungsgemeinschaft. Since 1996, he has been director and scientific member at the Max Planck Institute for Mathematics in the Sciences in Leipzig. After more than 10 years of work in Bochum, this he follo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leipzig
Leipzig (, ; ; Upper Saxon: ; ) is the most populous city in the States of Germany, German state of Saxony. The city has a population of 628,718 inhabitants as of 2023. It is the List of cities in Germany by population, eighth-largest city in Germany and is part of the Central German Metropolitan Region. The name of the city is usually interpreted as a Slavic term meaning ''place of linden trees'', in line with many other Slavic placenames in the region. Leipzig is located about southwest of Berlin, in the southernmost part of the North German Plain (the Leipzig Bay), at the confluence of the White Elster and its tributaries Pleiße and Parthe. The Leipzig Riverside Forest, Europe's largest intra-city riparian forest, has developed along these rivers. Leipzig is at the centre of Neuseenland (''new lake district''). This district has Bodies of water in Leipzig, several artificial lakes created from former lignite Open-pit_mining, open-pit mines. Leipzig has been a trade city s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Science
A material is a substance or mixture of substances that constitutes an object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical and chemical properties, or on their geological origin or biological function. Materials science is the study of materials, their properties and their applications. Raw materials can be processed in different ways to influence their properties, by purification, shaping or the introduction of other materials. New materials can be produced from raw materials by synthesis. In industry, materials are inputs to manufacturing processes to produce products or more complex materials, and the nature and quantity of materials used may form part of the calculation for the cost of a product or delivery under contract, such as where contract costs are calculated on a " time and materials" basis. Historical elements Materials chart the history of humanity. The system of the three prehist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |