|
List Of Things Named After Lev Landau
{{Short description, none Lev Landau (1908 – 1968), Soviet physicist who made fundamental contributions to many areas of theoretical physics, is the eponym of the topics in physics listed below. Physics *Darrieus–Landau instability *DLVO theory, Derjaguin–Landau–Verwey–Overbeek theory *Ivanenko–Landau–Kähler equation *Ginzburg–Landau theory *Guderley–Landau–Stanyukovich problem *Landau damping *Landau derivative *Diamagnetism#In_metals, Landau diamagnetism *Landau distribution *Fermi liquid theory, Landau's Fermi-liquid theory *Landau gauge *Landau kinetic equation *Landau theory, Landau's phase transition theory *Landau pole *Landau potential *S-matrix_theory#Basic_principles, Landau principle *Landau quantization or Landau quantization, Landau levels *Landau–Hopf theory of turbulence *Landau-Levich problem *Landau–Lifshitz model *Landau-Lifshitz pseudotensor *Landau–Lifshitz–Gilbert equation *Aeroacoustics, Landau–Lifshitz aeroacoustic equation *L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lev Landau
Lev Davidovich Landau (russian: Лев Дави́дович Ланда́у; 22 January 1908 – 1 April 1968) was a Soviet-Azerbaijani physicist of Jewish descent who made fundamental contributions to many areas of theoretical physics. His accomplishments include the independent co-discovery of the density matrix method in quantum mechanics (alongside John von Neumann), the quantum mechanical theory of diamagnetism, the theory of superfluidity, the theory of second-order phase transitions, the Ginzburg–Landau theory of superconductivity, the theory of Fermi liquids, the explanation of Landau damping in plasma physics, the Landau pole in quantum electrodynamics, the two-component theory of neutrinos, and Landau's equations for ''S'' matrix singularities. He received the 1962 Nobel Prize in Physics for his development of a mathematical theory of superfluidity that accounts for the properties of liquid helium II at a temperature below (). Life Early years Landau was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
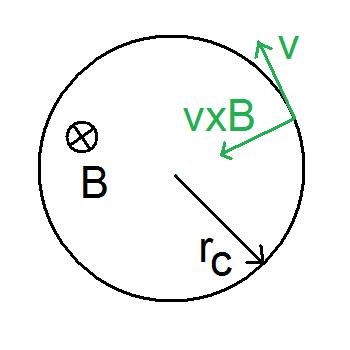
Landau Quantization
In quantum mechanics, Landau quantization refers to the quantization of the cyclotron orbits of charged particles in a uniform magnetic field. As a result, the charged particles can only occupy orbits with discrete, equidistant energy values, called Landau levels. These levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. It is named after the Soviet physicist Lev Landau. Landau quantization is directly responsible for the electronic susceptibility of metals, known as Landau diamagnetism. Under strong magnetic fields, Landau quantization leads to oscillations in electronic properties of materials as a function of the applied magnetic field known as De Haas–Van Alphen and Shubnikov–de Haas effects. Landau quantization is a key ingredient to explain the integer quantum Hall effect. Derivation Consider a system of non-interacting particles with charge and spin confined to an area in the plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Zener Formula
The Landau–Zener formula is an analytic solution to the equations of motion governing the transition dynamics of a two-state quantum system, with a time-dependent Hamiltonian varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic (not adiabatic) transition between the two energy states, was published separately by Lev Landau, Clarence Zener, Ernst Stueckelberg, and Ettore Majorana, in 1932. If the system starts, in the infinite past, in the lower energy eigenstate, we wish to calculate the probability of finding the system in the upper energy eigenstate in the infinite future (a so-called Landau–Zener transition). For infinitely slow variation of the energy difference (that is, a Landau–Zener velocity of zero), the adiabatic theorem tells us that no such transition will take place, as the system will always be in an instantaneous eigenstate of the Hamiltonian at that moment in time. At non ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Yang Theorem
In quantum mechanics, the Landau–Yang theorem is a selection rule for particles that decay into two on-shell photons. The theorem states that a massive particle with spin 1 cannot decay into two photons. Assumptions A photon here is any particle with spin 1, without mass and without internal degrees of freedom. The photon is the only known particle with these properties. Consequences The theorem has several consequences in particle physics. For example: * The meson ρ cannot decay into two photons, differently from the neutral pion, that almost always decays into this final state (98.8% of times). * The boson Z cannot decay into two photons. * The Higgs boson The Higgs boson, sometimes called the Higgs particle, is an elementary particle in the Standard Model of particle physics produced by the quantum excitation of the Higgs field, one of the fields in particle physics theory. In the St ..., whose spin was not measured before 2013, but whose decay into ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau-Raychaudhuri Equation
In general relativity, the Raychaudhuri equation, or Landau–Raychaudhuri equation, is a fundamental result describing the motion of nearby bits of matter. The equation is important as a fundamental lemma for the Penrose–Hawking singularity theorems and for the study of exact solutions in general relativity, but has independent interest, since it offers a simple and general validation of our intuitive expectation that gravitation should be a universal attractive force between any two bits of mass-energy in general relativity, as it is in Newton's theory of gravitation. The equation was discovered independently by the Indian physicist Amal Kumar Raychaudhuri and the Soviet physicist Lev Landau.''The large scale structure of space-time'' by Stephen W. Hawking and G. F. R. Ellis, Cambridge University Press, 1973, p. 84, . Mathematical statement Given a timelike unit vector field \vec (which can be interpreted as a family or congruence of nonintersecting world lines via the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Pomeranchuk–Migdal Effect
In high-energy physics, the Landau–Pomeranchuk–Migdal effect, also known as the Landau–Pomeranchuk effect and the Pomeranchuk effect, or simply LPM effect, is a reduction of the bremsstrahlung and pair production cross sections at high energies or high matter densities. It is named in honor to Lev Landau, Isaak Pomeranchuk and Arkady Migdal. Overview A high energy particle undergoing multiple soft scatterings from a medium will experience interference effects between adjacent scattering sites. From uncertainty as the longitudinal momentum transfer gets small the particles wavelength will increase, if the wavelength becomes longer than the mean free path in the medium (the average distance between scattering sites) then the scatterings can no longer be treated as independent events, this is the LPM effect. The Bethe–Heitler spectrum for multiple scattering induced radiation assumes that the scatterings are independent, the quantum interference between successive scatterings c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Placzek Ratio
Landau–Placzek ratio is a ratio of the integrated intensity of Rayleigh scattering to the combined integrated intensity of Brillouin scattering of a triplet frequency spectrum of light scattered by homogenous liquids or gases. The triplet consists of two frequency shifted Brillouin scattering and a central unshifted Rayleigh scattering line split. The triplet structure was explained by Lev Landau and George Placzek in 1934 in a short publication, summarizing major results of their analysis. Landau and Placzek noted in their short paper that a more detailed discussion will be published later although that paper does not seem to have been published. However, a detailed discussion is provided in Lev Landau and Evgeny Lifshitz's book. The Landau–Placzek ratio is defined as :R_ = \frac where *I_c is the integral intensity of central Rayleigh peak *I_B is the integral intensity of Brillouin peak. The Landau–Placzek formula provides an approximate theoretical prediction for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Peierls Instability
Landau–Peierls instability refers to the phenomenon in which the mean square displacements due to thermal fluctuatuions diverge in the thermodynamic limit and is named after Lev Landau (1937) and Rudolf Peierls (1934). This instability prevails in one-dimensional ordering of atoms/molecules in 3D space such as 1D crystals and smectics and also in two-dimensional ordering in 2D space such as a monomolecular adsorbed filsms at the interface between two isotrophic phases. The divergence is logarthmic, which is rather slow and therefore it is possible to realize substances (such as the smectics) in practice that are subject to Landau–Peierls instability. Mathematical description Consider a one-dimensionally ordered crystal in 3D space. The density function is then given by \rho=\rho(z). Since this is a 1D system, only the displacement u along the z-direction due to thermal fluctuations can smooth out the density function; displacements in other two directions are irrelevant. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aeroacoustics
Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects. Although no complete scientific theory of the generation of noise by aerodynamic flows has been established, most practical aeroacoustic analysis relies upon the so-called ''aeroacoustic analogy'', proposed by Sir James Lighthill in the 1950s while at the University of Manchester. whereby the governing equations of motion of the fluid are coerced into a form reminiscent of the wave equation of "classical" (i.e. linear) acoustics in the left-hand side with the remaining terms as sources in the right-hand side. History The modern discipline of aeroacoustics can be said to have originated with the first publication of Lighthill in the early 1950s, when noise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Lifshitz–Gilbert Equation
In physics, the Landau–Lifshitz–Gilbert equation, named for Lev Landau, Evgeny Lifshitz, and T. L. Gilbert, is a name used for a differential equation describing the precessional motion of magnetization in a solid. It is a modification by Gilbert of the original equation of Landau and Lifshitz. The various forms of the equation are commonly used in micromagnetics to model the effects of a magnetic field on ferromagnetic materials. In particular it can be used to model the time domain behavior of magnetic elements due to a magnetic field. An additional term was added to the equation to describe the effect of spin polarized current on magnets. Landau–Lifshitz equation In a ferromagnet, the magnetization can vary internally but at each point its magnitude is equal to the saturation magnetization . The Landau–Lifshitz–Gilbert equation predicts the rotation of the magnetization in response to torques. An earlier, but equivalent, equation (the Landau–Lifshitz equation) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |