|
List Of Things Named After James Clerk Maxwell
This is a list of things named for James Clerk Maxwell. Science * MaxwellŌĆōBetti reciprocal work theorem * MaxwellŌĆōBloch equations * MaxwellŌĆōHuberŌĆōHenckyŌĆōvon Mises theory * Maxwell coupling * MaxwellŌĆōCremona correspondence ** CremonaŌĆōMaxwell diagram * Maxwell's discs * Maxwell's theorem * Maxwell's theorem (geometry) * Maxwell's Wheel * Maxwell's fisheye lens Electromagnetism * MaxwellŌĆōWagnerŌĆōSillars polarization * MaxwellŌĆōWien bridge, see Maxwell bridge * Maxwell bivector * Maxwell bridge * Maxwell coil * Maxwell displacement current * Maxwell's equations (electromagnetism) ** MaxwellŌĆōProca equation ** MaxwellŌĆōAmpere law * The maxwell (Mx), a compound derived CGS unit measuring magnetic flux * Maxwell tensor, also Maxwell stress tensor * MaxwellŌĆōLodge effect Thermodynamics and kinetic theory * MaxwellŌĆōBoltzmann statistics ** MaxwellŌĆōBoltzmann distribution (statistical thermodynamics), also known as Maxwellian curve, or Maxwellian for sho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 ŌĆō 5 November 1879) was a Scottish mathematician and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the " second great unification in physics" where the first one had been realised by Isaac Newton. With the publication of " A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society. His statement that "light and magnetism are affections of the same substance" is at page 499.) The unification of light and electri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Equations
Maxwell's equations, or MaxwellŌĆōHeaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric field, electric and magnetic fields are generated by electric charge, charges, electric current, currents, and changes of the fields.''Electric'' and ''magnetic'' fields, according to the theory of relativity, are the components of a single electromagnetic field. The equations are named after the physicist and mathematician James Clerk Maxwell, who, in 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon. The modern f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Thermodynamic Surface
MaxwellŌĆÖs thermodynamic surface is an 1874 sculpture made by Scottish physicist James Clerk Maxwell (1831ŌĆō1879). This model provides a three-dimensional space of the various states of a fictitious substance with water-like properties. This plot has coordinates volume (x), entropy (y), and energy (z). It was based on the American scientist Josiah Willard GibbsŌĆÖ graphical thermodynamics papers of 1873. The model, in Maxwell's words, allowed "the principal features of known substances obe represented on a convenient scale." Construction of the model Gibbs' papers defined what Gibbs called the "thermodynamic surface," which expressed the relationship between the volume, entropy, and energy of a substance at different temperatures and pressures. However, Gibbs did not include any diagrams of this surface. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell's Relations
file:Thermodynamic map.svg, 400px, Flow chart showing the paths between the Maxwell relations. P is pressure, T temperature, V volume, S entropy, \alpha coefficient of thermal expansion, \kappa compressibility, C_V heat capacity at constant volume, C_P heat capacity at constant pressure. Maxwell's relations are a set of equations in thermodynamics which are derivable from the symmetry of second derivatives and from the definitions of the thermodynamic potentials. These relations are named for the nineteenth-century physicist James Clerk Maxwell. Equations The structure of Maxwell relations is a statement of equality among the second derivatives for continuous functions. It follows directly from the fact that the order of differentiation of an analytic function of two variables is irrelevant ( Schwarz theorem). In the case of Maxwell relations the function considered is a thermodynamic potential and x_i and x_j are two different natural variables for that potential, we ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
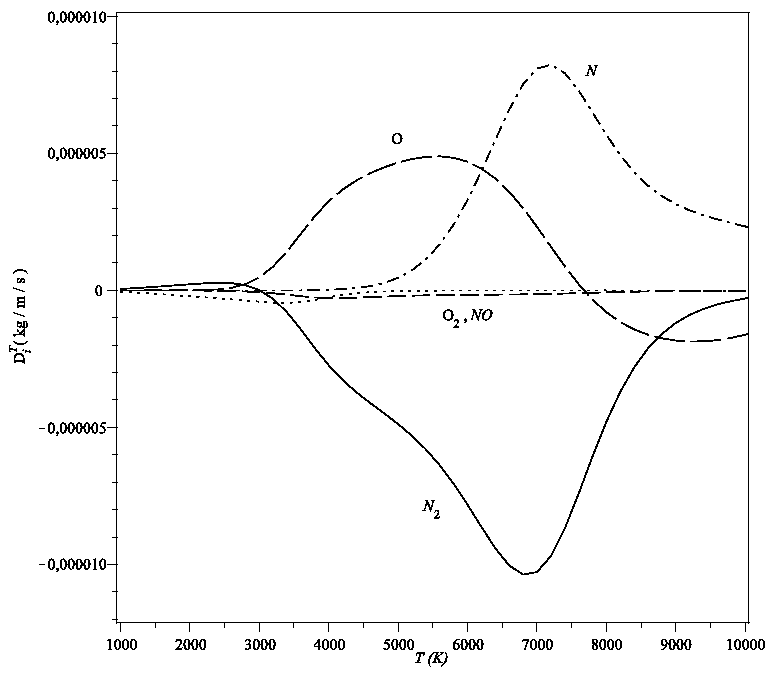
MaxwellŌĆōStefan Diffusion
The MaxwellŌĆōStefan diffusion (or StefanŌĆōMaxwell diffusion) is a model for describing diffusion in multicomponent systems. The equations that describe these transport processes have been developed independently and in parallel by James Clerk MaxwellJ. C. Maxwell: ''On the dynamical theory of gases'', The Scientific Papers of J. C. Maxwell, 1965, 2, 26ŌĆō78. for dilute gases and Josef StefanJ. Stefan: ''├£ber das Gleichgewicht und Bewegung, insbesondere die Diffusion von Gemischen'', Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften Wien, 2te Abteilung a, 1871, 63, 63-124. for liquids. The MaxwellŌĆōStefan equation is \frac = \nabla \ln a_i = \sum_^ = \sum_^ * Ōłć: vector differential operator * Žć: Mole fraction * ╬╝: Chemical potential * a: Activity * i, j: Indexes for component i and j * n: Number of components * \mathfrak_: MaxwellŌĆōStefan-diffusion coefficient * \vec v_i: Diffusion velocity of component i * c_i: Molar concentration of component i * c: Total ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxwellŌĆōJ├╝ttner Distribution
In physics, the MaxwellŌĆōJ├╝ttner distribution is the distribution of speeds of particles in a hypothetical gas of relativistic particles. Similar to Maxwell's distribution, the MaxwellŌĆōJ├╝ttner distribution considers a classical ideal gas where the particles are dilute and do not significantly interact with each other. The distinction from Maxwell's case is that effects of special relativity are taken into account. In the limit of low temperatures T much less than mc^2/k (where m is the mass of the kind of particle making up the gas, c is the speed of light and k is Boltzmann's constant), this distribution becomes identical to the MaxwellŌĆōBoltzmann distribution. The distribution can be attributed to Ferencz J├╝ttner, who derived it in 1911. It has become known as the MaxwellŌĆōJ├╝ttner distribution by analogy to the name Maxwell-Boltzmann distribution that is commonly used to refer to Maxwell's distribution. Definition As the gas becomes hotter and kT approaches or excee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxwellŌĆōBoltzmann Distribution
In physics (in particular in statistical mechanics), the MaxwellŌĆōBoltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used for describing particle speeds in idealized gases, where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. The term "particle" in this context refers to gaseous particles only ( atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.''Statistical Physics'' (2nd Edition), F. Mandl, Manchester Physics, John Wiley & Sons, 2008, The energies of such particles follow what is known as MaxwellŌĆōBoltzmann statistics, and the statistical distribution of speeds is derived by equating particle energies with kinetic energy. Mathem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxwellŌĆōBoltzmann Statistics
In statistical mechanics, MaxwellŌĆōBoltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible. The expected number of particles with energy \varepsilon_i for MaxwellŌĆōBoltzmann statistics is :\langle N_i \rangle = \frac = \frac\,g_i e^, where: *\varepsilon_i is the energy of the ''i''-th energy level, *\langle N_i \rangle is the average number of particles in the set of states with energy \varepsilon_i, *g_i is the degeneracy of energy level ''i'', that is, the number of states with energy \varepsilon_i which may nevertheless be distinguished from each other by some other means,For example, two simple point particles may have the same energy, but different momentum vectors. They may be distinguished from each other on this basis, and the degeneracy will be the number of poss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxwellŌĆōLodge Effect
The Maxwell-Lodge effect is a phenomenon of electromagnetic induction in which an electric charge, near a solenoid in which current changes slowly, feels an electromotive force (e.m.f.) even if the magnetic field is practically static inside and null outside. It can be considered a classical analogue of the quantum mechanical AharonovŌĆōBohm effect, where instead the field is exactly static inside and null outside. The term appeared in the scientific literature in a 2008 article, referring to an article of 1889 by physicist Oliver Lodge. Description Consider an infinite solenoid (ideal solenoid) with ''n'' turns per length unit, through which a current I(t) flows. The magnetic field inside the solenoid is, : \mathbf B = \mu n I(t) (1) while the field outside the solenoid is null. From the second and third Maxwell's equations, : \begin \nabla \times \mathbf &= -\dfrac \\ \nabla \cdot \mathbf &= 0 \end and from definitions of magnetic potential and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell Stress Tensor
The Maxwell stress tensor (named after James Clerk Maxwell) is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand. In the relativistic formulation of electromagnetism, the Maxwell's tensor appears as a part of the electromagnetic stressŌĆōenergy tensor which is the electromagnetic component of the total stressŌĆōenergy tensor. The latter describes the density and flux of energy and momentum in spacetime. Motivatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Flux
In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field B over that surface. It is usually denoted or . The SI unit of magnetic flux is the weber (Wb; in derived units, voltŌĆōseconds), and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils and electronics, that evaluates the change of voltage in the measuring coils to calculate the measurement of magnetic flux. Description The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force). Since a vector field is quite difficult to visualize at first, in elementary physics one may instead visualize this field with field lines. The magnetic flux through some surface, in this simplified picture, is proportional to the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |