|
List Of Spacetimes
This is a list of well-known spacetimes in general relativity. Where the metric tensor is given, a particular choice of coordinates is used, but there are often other useful choices of coordinate available. In general relativity, spacetime is described mathematically by a metric tensor (on a smooth manifold), conventionally denoted g or ds^2. This metric is sufficient to formulate the vacuum Einstein field equations. If matter is included, described by a stress-energy tensor, then one has the Einstein field equations with matter. On certain regions of spacetime (and possibly the entire spacetime) one can describe the points by a set of coordinate chart, coordinates. In this case, the metric can be written down in terms of the coordinates, or more precisely, the coordinate one-forms and coordinates. During the course of the development of the field of general relativity, a number of explicit metrics have been found which satisfy the Einstein field equations, a number of which are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur. Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The physicist Albert Einstein helped develop the idea of spacetime as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Einstein based a work on special relativity on two postulates: * The laws of physics are invari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Sitter Space
In mathematical physics, ''n''-dimensional de Sitter space (often abbreviated to dS''n'') is a maximally symmetric Lorentzian manifold with constant positive scalar curvature. It is the Lorentzian analogue of an ''n''-sphere (with its canonical Riemannian metric). The main application of de Sitter space is its use in general relativity, where it serves as one of the simplest mathematical models of the universe consistent with the observed accelerating expansion of the universe. More specifically, de Sitter space is the maximally symmetric vacuum solution of Einstein's field equations with a positive cosmological constant \Lambda (corresponding to a positive vacuum energy density and negative pressure). There is cosmological evidence that the universe itself is asymptotically de Sitter, i.e. it will evolve like the de Sitter universe in the far future when dark energy dominates. de Sitter space and anti-de Sitter space are named after Willem de& ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pp-wave Spacetime
In general relativity, the pp-wave spacetimes, or pp-waves for short, are an important family of exact solutions of Einstein's field equation. The term ''pp'' stands for ''plane-fronted waves with parallel propagation'', and was introduced in 1962 by Jürgen Ehlers and Wolfgang Kundt. Overview The pp-waves solutions model radiation moving at the speed of light. This radiation may consist of: * electromagnetic radiation, * gravitational radiation, * massless radiation associated with Weyl fermions, * ''massless'' radiation associated with some hypothetical distinct type relativistic classical field, or any combination of these, so long as the radiation is all moving in the ''same'' direction. A special type of pp-wave spacetime, the plane wave spacetimes, provide the most general analogue in general relativity of the plane waves familiar to students of electromagnetism. In particular, in general relativity, we must take into account the gravitational effects of the energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemaître–Tolman Metric
In physics, the Lemaître–Tolman metric, also known as the Lemaître–Tolman–Bondi metric or the Tolman metric, is a Lorentzian metric based on an exact solution of Einstein's field equations; it describes an isotropic and expanding (or contracting) universe which is not homogeneous, and is thus used in cosmology as an alternative to the standard Friedmann–Lemaître–Robertson–Walker metric to model the expansion of the universe. It has also been used to model a universe which has a fractal distribution of matter to explain the accelerating expansion of the universe. It was first found by Georges Lemaître in 1933 and Richard Tolman in 1934 and later investigated by Hermann Bondi in 1947. Details In a synchronous reference system where g_=1 and g_=0, the time coordinate x^0=t (we set G=c=1) is also the proper time \tau=\sqrt x^0 and clocks at all points can be synchronized. For a dust-like medium where the pressure is zero, dust particles move freely i.e., along th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boyer–Lindquist Coordinates
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole. The Hamiltonian for test particle motion in Kerr spacetime is separable in Boyer–Lindquist coordinates. Using Hamilton–Jacobi theory one can derive a fourth constant of the motion known as Carter's constant. The 1967 paper introducing Boyer–Lindquist coordinates was a posthumous publication for Robert H. Boyer, who was killed in the 1966 University of Texas tower shooting. Line element The line element for a black hole with a total mass equivalent M, angular momentum J, and charge Q in Boyer–Lindquist coordinates and natural units (G=c=1) is : ds^2 = -\frac\left(dt - a \sin^2\theta \,d\phi \right)^2 +\frac\Big(\left(r^2+a^2\right)\,d\phi - a \,dt\Big)^2 + \fracdr^2 + \rho^2 \,d\theta^2 where :\Delta = r^2 - 2Mr + a^2 + Q^2, called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerr–Newman Metric
The Kerr–Newman metric is the most general asymptotically flat, stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions, that is, of solutions to the Einstein–Maxwell equations which account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions. This solution has not been especially useful for describing astrophysical phenomena, because observed astronomical objects do not possess an appreciable net electric charge, and the magnetic fields of stars arise through other processes. As a model of realistic black ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
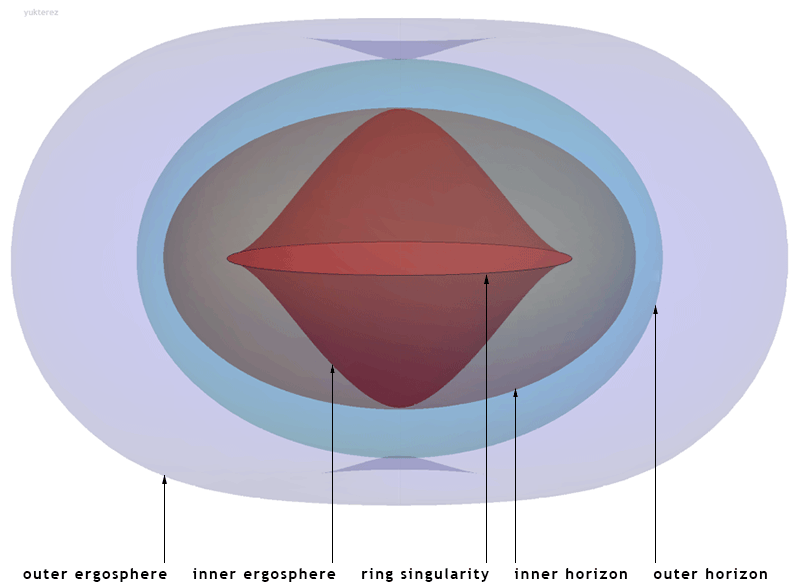
Kerr Spacetime
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black hole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Function
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0. An implicit function is a function that is defined by an implicit equation, that relates one of the variables, considered as the value of the function, with the others considered as the arguments. For example, the equation x^2 + y^2 - 1 = 0 of the unit circle defines as an implicit function of if , and is restricted to nonnegative values. The implicit function theorem provides conditions under which some kinds of implicit equations define implicit functions, namely those that are obtained by equating to zero multivariable functions that are continuously differentiable. Examples Inverse functions A common type of implicit function is an inverse function. Not all functions have a unique inverse function. If is a function of that has a unique inv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kruskal–Szekeres Coordinates
In general relativity, Kruskal–Szekeres coordinates, named after Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole. These coordinates have the advantage that they cover the entire spacetime manifold of the maximally extended Schwarzschild solution and are well-behaved everywhere outside the physical singularity. There is no misleading coordinate singularity at the horizon. The Kruskal–Szekeres coordinates also apply to space-time around a spherical object, but in that case do not give a description of space-time inside the radius of the object. Space-time in a region where a star is collapsing into a black hole is approximated by the Kruskal–Szekeres coordinates (or by the Schwarzschild coordinates). The surface of the star remains outside the event horizon in the Schwarzschild coordinates, but crosses it in the Kruskal–Szekeres coordinates. (In any "black hole" which we observe, we see it at a time when its m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |