|
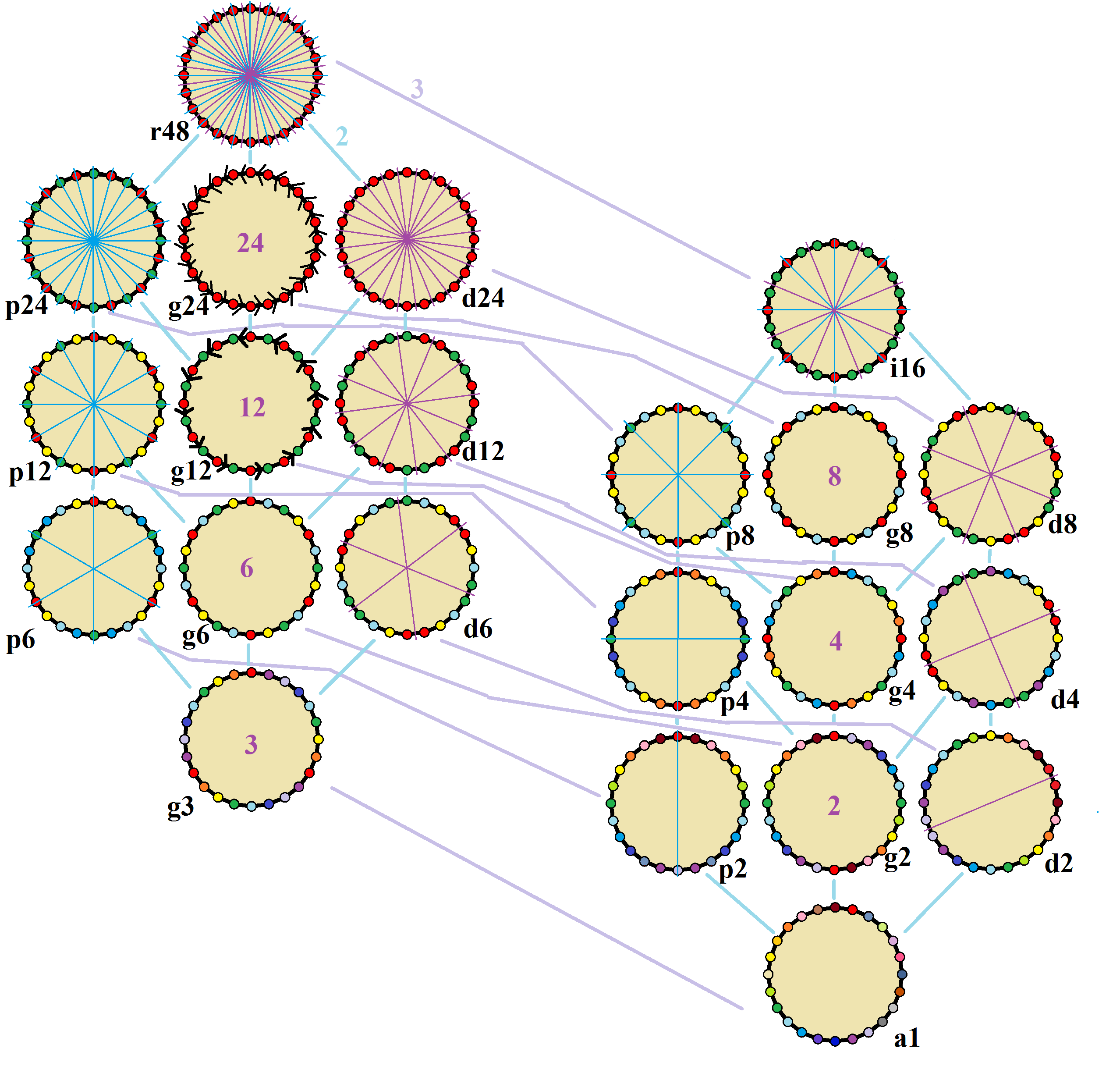
List Of Self-intersecting Polygons
Self-intersecting polygons, crossed polygons, or self-crossing polygons are polygons some of whose edges cross each other. They contrast with simple polygons, whose edges never cross. Some types of self-intersecting polygons are: *the crossed quadrilateral, with four edges **the antiparallelogram, a crossed quadrilateral with alternate edges of equal length ***the crossed rectangle, an antiparallelogram whose edges are two opposite sides and the two diagonals of a rectangle, hence having two edges parallel * Star polygons ** pentagram, with five edges ** hexagram, with six edges ** heptagram, with seven edges ** octagram, with eight edges ** enneagram or nonagram, with nine edges ** decagram, with ten edges ** hendecagram, with eleven edges **dodecagram, with twelve edges ** icositetragram, with twenty four edges ** 257-gram, with two hundred and fifty seven edges See also * *Complex polygon The term ''complex polygon'' can mean two different things: * In geometry, a polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octagram
In geometry, an octagram is an eight-angled star polygon. The name ''octagram'' combine a Greek numeral prefix, ''wikt:octa-, octa-'', with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''-gram'' suffix derives from γραμμή (''grammḗ'') meaning "line". Detail In general, an octagram is any self-intersecting octagon (8-sided polygon). The regular polygon, regular octagram is labeled by the Schläfli symbol , which means an 8-sided star, connected by every third point. Variations These variations have a lower dihedral, Dih4, symmetry: The symbol Rub el Hizb is a Unicode glyph ۞ at U+06DE. As a quasitruncated square Deeper truncations of the square can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths. A truncated square is an octagon, t=. A quasitruncated square, inverted as , is an octagram, t=.The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Polygon
The term ''complex polygon'' can mean two different things: * In geometry, a polygon in the unitary plane, which has two complex dimensions. * In computer graphics, a polygon whose boundary is not simple. Geometry In geometry, a complex polygon is a polygon in the complex Hilbert plane, which has two complex dimensions. A complex number may be represented in the form (a + ib), where a and b are real numbers, and i is the square root of -1. Multiples of i such as ib are called ''imaginary numbers''. A complex number lies in a complex plane having one real and one imaginary dimension, which may be represented as an Argand diagram. So a single complex dimension comprises two spatial dimensions, but of different kinds - one real and the other imaginary. The unitary plane comprises two such complex planes, which are orthogonal to each other. Thus it has two real dimensions and two imaginary dimensions. A complex polygon is a (complex) two-dimensional (i.e. four spatial dime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
257-gon
In geometry, a 257-gon is a polygon with 257 sides. The sum of the interior angles of any non- self-intersecting 257-gon is 45,900°. Regular 257-gon The area of a regular 257-gon is (with ) :A = \frac t^2 \cot \frac\approx 5255.751t^2. A whole regular 257-gon is not visually discernible from a circle, and its perimeter differs from that of the circumscribed circle by about 24 parts per million. Construction The regular 257-gon (one with all sides equal and all angles equal) is of interest for being a constructible polygon: that is, it can be constructed using a compass and an unmarked straightedge. This is because 257 is a Fermat prime, being of the form 22''n'' + 1 (in this case ''n'' = 3). Thus, the values \cos \frac and \cos \frac are 128-degree algebraic numbers, and like all constructible numbers they can be written using square roots and no higher-order roots. Although it was known to Gauss by 1801 that the regular 257-gon was constructible, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icositetragram
In geometry, an icositetragon (or icosikaitetragon) or 24-gon is a twenty-four-sided polygon. The sum of any icositetragon's interior angles is 3960 degrees. Regular icositetragon The ''regular polygon, regular icositetragon'' is represented by Schläfli symbol and can also be constructed as a Truncation (geometry), truncated dodecagon, t, or a twice-truncated hexagon, tt, or thrice-truncated triangle, ttt. One interior angle in a regular polygon, regular icositetragon is 165°, meaning that one exterior angle would be 15°. The area of a regular icositetragon is: (with ''t'' = edge length) : A = 6t^2 \cot \frac = t^2(2+\sqrt+\sqrt+\sqrt). The icositetragon appeared in Archimedes' polygon approximation of pi, along with the hexagon (6-gon), dodecagon (12-gon), tetracontaoctagon (48-gon), and enneacontahexagon (96-gon). Construction As 24 = 23 × 3, a regular icositetragon is constructible polygon, constructible using a compass and straightedge. As a truncated dodecagon, it ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecagram
In geometry, a dodecagram ( Henry George Liddell, Robert Scott, ''A Greek-English Lexicon'', on Perseus) is a star polygon or compound with 12 vertex (geometry), vertices. There is one regular dodecagram polygon (with Schläfli symbol and a turning number of 5). There are also 4 regular compounds and Regular dodecagram There is one regular form: , containing 12 vertices, with a turning number of 5. A regular dodecagram has the same vertex arrangement as a regular dodecagon, which may be regarded as .Dodecagrams as regular compounds There are four regular dodecagram star figure, star figures: =2, =3, =4, and =6. The first is a compound of two hexagon, hexagons, the second is a compound of three square (geometry), squares, the third is a co ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hendecagram
In geometry, a hendecagram (also endecagram or endekagram) is a star polygon that has eleven Vertex (geometry), vertices. The name ''hendecagram'' combines a Greek numeral prefix, ''wikt:hendeca-, hendeca-'', with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''hendeca-'' prefix derives from Greek ἕνδεκα (ἕν + δέκα, one + ten) meaning "11 (number), eleven". The ''-gram'' suffix derives from γραμμῆς (''grammēs'') meaning a line. Regular hendecagrams There are four regular hendecagrams, which can be described by the notation , , , and ; in this notation, the number after the slash indicates the number of steps between pairs of points that are connected by edges. These same four forms can also be considered as Stellation#Stellating polygons, stellations of a regular hendecagon. Since 11 is prime, all hendecagrams are star polygons and not compound figures. Construction As with all odd regular polygons and star polygons whose orders are not produ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decagram (geometry)
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is . The name ''decagram'' combines a numeral prefix, ''wikt:deca-, deca-'', with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''-gram'' suffix derives from ''γραμμῆς'' (''grammēs'') meaning a line. Regular decagram For a regular decagram with unit edge lengths, the proportions of the crossing points on each edge are as shown below. Applications Decagrams have been used as one of the decorative motifs in girih tiles. : Isotoxal variations An isotoxal polygon has two vertices and one edge. There are isotoxal decagram forms, which alternates vertices at two radii. Each form has a freedom of one angle. The first is a variation of a double-wound of a pentagon , and last is a variation of a double-wound of a pentagram . The middle is a variation of a regular decagram, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enneagram (geometry)
In geometry, an enneagram (🟙 U+1F7D9) is a nine-pointed plane figure. It is sometimes called a nonagram, nonangle, or enneagon. The word 'enneagram' combines the numeral prefix ''wikt:ennea-, ennea-'' with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''gram'' suffix derives from ''γραμμῆ'' (''grammē'') meaning a line. Regular enneagram A regular enneagram is a 9-sided star polygon. It is constructed using the same points as the regular enneagon, but the points are connected in fixed steps. Two forms of regular enneagram exist: *One form connects every second point and is represented by the Schläfli symbol . *The other form connects every fourth point and is represented by the Schläfli symbol . There is also a star figure, or 3, made from the regular enneagon points but connected as a compound of three equilateral triangles. (If the triangles are alternately interlaced, this results in a Brunnian link.) This star figure is sometimes known as the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptagram
A heptagram, septagram, septegram or septogram is a seven-point star polygon, star drawn with seven straight strokes. The name ''heptagram'' combines a numeral prefix, ''hepta-'', with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''-gram'' suffix derives from ''γραμμῆ'' (''grammē'') meaning a line. Geometry In general, a heptagram is any self-intersecting heptagon (7-sided polygon). There are two ''regular'' heptagrams, labeled as and , with the second number representing the vertex interval step from a regular heptagon, . This is the smallest star polygon that can be drawn in two forms, as irreducible fractions. The two heptagrams are sometimes called the ''heptagram'' (for ) and the ''great heptagram'' (for ). The previous one, the regular hexagram , is a compound of two triangles. The smallest star polygon is the pentagram. The next one is the octagram and its related star figure (a compound of two squares), followed by the regular enneag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge (geometry)
In geometry, an edge is a particular type of line segment joining two vertex (geometry), vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two Face (geometry), faces (or polyhedron sides) meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal. An ''edge'' may also be an infinite line (geometry), line separating two half-planes. The ''sides'' of a plane angle are semi-infinite Half-line (geometry), half-lines (or rays). Relation to edges in graphs In graph theory, an Edge (graph theory), edge is an abstract object connecting two vertex (graph theory), graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment. However, any polyhedron can be represented by its n-s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
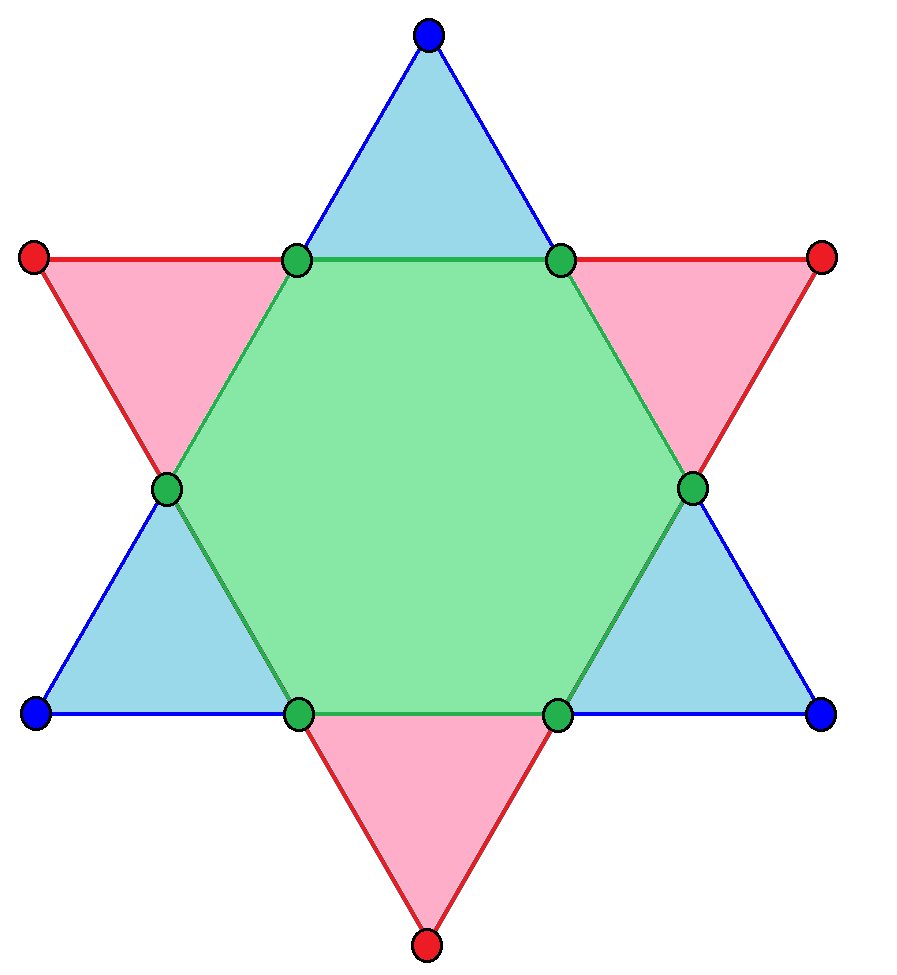
Hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green). A hexagram (Greek language, Greek) or sexagram (Latin language, Latin) is a six-pointed geometric star figure with the Schläfli symbol , 2, or . The term is used to refer to a compound figure of two equilateral triangles. The intersection is a regular hexagon. The hexagram is part of an infinite series of shapes which are compounds of two n-dimensional simplex, simplices. In three dimensions, Compound of two tetrahedra, the analogous compound is the stellated octahedron, and in four dimensions the compound of two 5-cells is obtained. It has been historically used in various religious and cultural contexts and as decorative motifs. The symbol was used as a decorative motif in medieval Christian churches and Jewish synagogues. In the medieval period, a Muslim mystical symbol known as the Seal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |