|
List Of B7 Polytopes
In 7-dimensional geometry, there are 128 uniform 7-polytope, uniform polytopes with B7 symmetry. There are two regular forms, the 7-orthoplex, and 8-cube with 14 and 128 vertices respectively. The 7-demicube is added with half of the symmetry. They can be visualized as symmetric orthographic projections in Coxeter planes of the B7 Coxeter group, and other subgroups. __TOC__ Graphs Symmetric orthographic projections of these 128 polytopes can be made in the B7, B6, B5, B4, B3, B2, A5, A3, Coxeter planes. Ak has ''[k+1]'' symmetry, and Bk has ''[2k]'' symmetry. These 128 polytopes are each shown in these 8 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position. References * Harold Scott MacDonald Coxeter, H.S.M. Coxeter: ** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 * Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
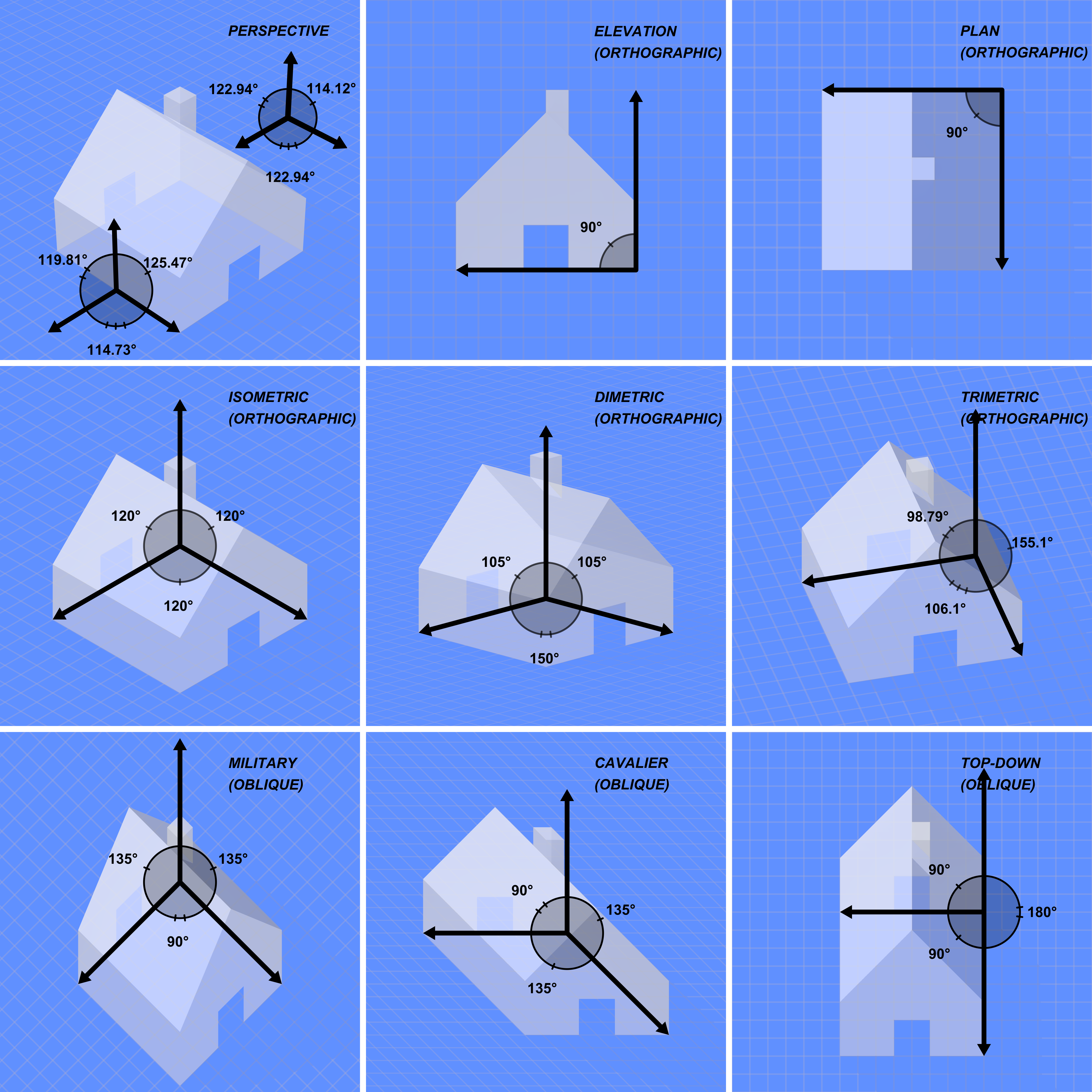
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Axonometric projection'' is synonymous with ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-cube T6 B4
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces. It can be named by its Schläfli symbol , being composed of 3 6-cubes around each 5-face. It can be called a hepteract, a portmanteau of tesseract (the ''4-cube'') and ''hepta'' for seven (dimensions) in Greek. It can also be called a regular tetradeca-7-tope or tetradecaexon, being a 7 dimensional polytope constructed from 14 regular facets. Related polytopes The ''7-cube'' is 7th in a series of hypercube: The dual of a 7-cube is called a 7-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the hepteract, creates another uniform polytope, called a demihepteract, (part of an infinite family called demihypercubes), which has 14 demihexeractic and 64 6-simplex 6-faces. As a configuration Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified 7-orthoplex
In seven-dimensional geometry, a rectified 7-orthoplex is a convex uniform 7-polytope, being a rectification of the regular 7-orthoplex. There are unique 7 degrees of rectifications, the zeroth being the 7-orthoplex, and the 6th and last being the 7-cube. Vertices of the rectified 7-orthoplex are located at the edge-centers of the 7-orthoplex. Vertices of the birectified 7-orthoplex are located in the triangular face centers of the 7-orthoplex. Vertices of the trirectified 7-orthoplex are located in the tetrahedral cell centers of the 7-orthoplex. Rectified 7-orthoplex The ''rectified 7-orthoplex'' is the vertex figure for the demihepteractic honeycomb. The rectified 7-orthoplex's 84 vertices represent the kissing number of a sphere-packing constructed from this honeycomb. : or Alternate names * rectified heptacross * rectified hecatonicosoctaexon (Acronym rez) (Jonathan Bowers) - rectified 128-faceted polyexon Images Construction There are two Coxeter groups ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-cube T5 A3
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces. It can be named by its Schläfli symbol , being composed of 3 6-cubes around each 5-face. It can be called a hepteract, a portmanteau of tesseract (the ''4-cube'') and ''hepta'' for seven (dimensions) in Greek. It can also be called a regular tetradeca-7-tope or tetradecaexon, being a 7 dimensional polytope constructed from 14 regular facets. Related polytopes The ''7-cube'' is 7th in a series of hypercube: The dual of a 7-cube is called a 7-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the hepteract, creates another uniform polytope, called a demihepteract, (part of an infinite family called demihypercubes), which has 14 demihexeractic and 64 6-simplex 6-faces. As a configuration Thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-cube T5
In geometry, a 7-cube is a seven-dimensional hypercube with 128 vertices, 448 edges, 672 square faces, 560 cubic cells, 280 tesseract 4-faces, 84 penteract 5-faces, and 14 hexeract 6-faces. It can be named by its Schläfli symbol , being composed of 3 6-cubes around each 5-face. It can be called a hepteract, a portmanteau of tesseract (the ''4-cube'') and ''hepta'' for seven (dimensions) in Greek. It can also be called a regular tetradeca-7-tope or tetradecaexon, being a 7 dimensional polytope constructed from 14 regular facets. Related polytopes The ''7-cube'' is 7th in a series of hypercube: The dual of a 7-cube is called a 7-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the hepteract, creates another uniform polytope, called a demihepteract, (part of an infinite family called demihypercubes), which has 14 demihexeractic and 64 6-simplex 6-faces. As a configuration Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |