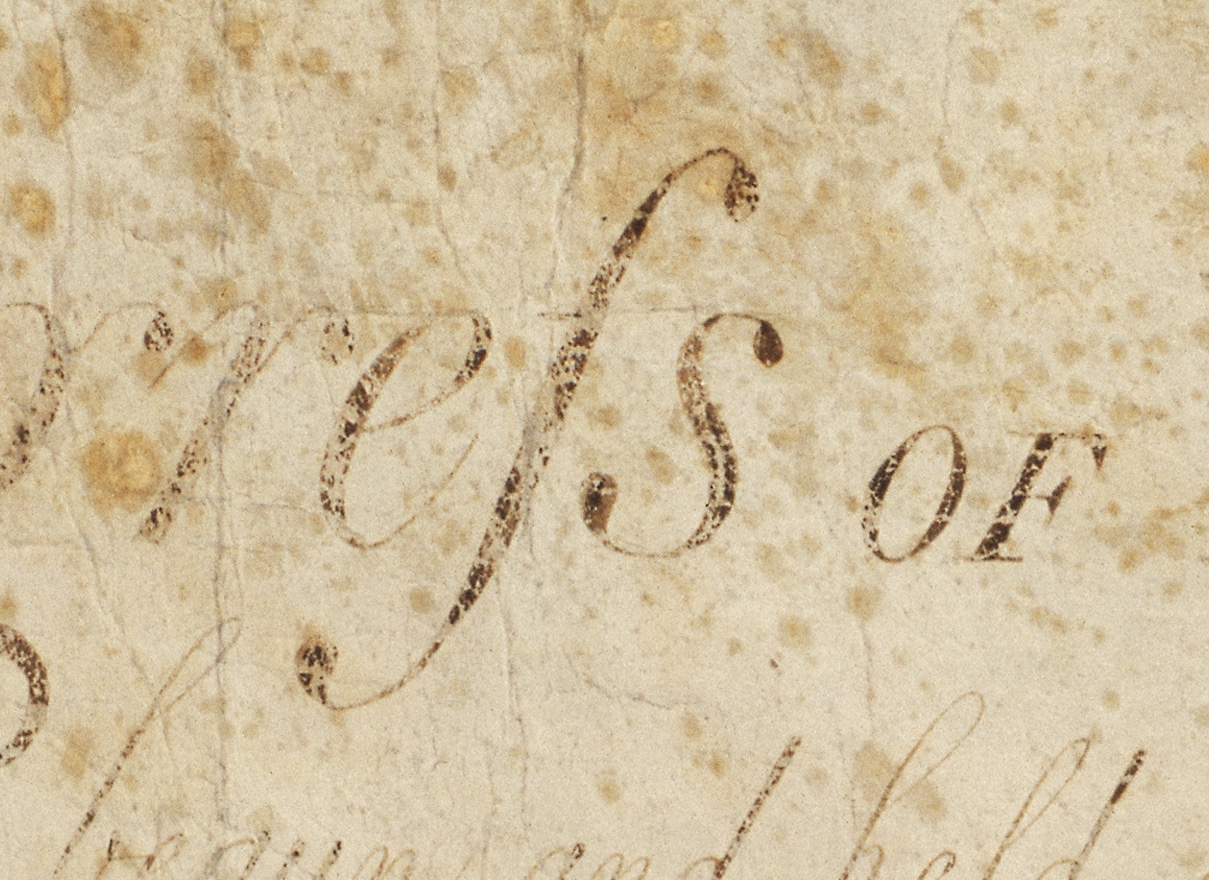|
Leibniz's Notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols and to represent infinitely small (or infinitesimal) increments of and , respectively, just as and represent finite increments of and , respectively. Consider as a function of a variable , or = . If this is the case, then the derivative of with respect to , which later came to be viewed as the limit :\lim_\frac = \lim_\frac, was, according to Leibniz, the quotient of an infinitesimal increment of by an infinitesimal increment of , or :\frac=f'(x), where the right hand side is Joseph-Louis Lagrange's notation for the derivative of at . The infinitesimal increments are called . Related to this is the integral in which the infinitesimal increments are summed (e.g. to compute lengths, areas and volumes as sums of tiny pieces), for which Leibniz also supplied a closely related notation involving the same differentials ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gottfried Wilhelm Leibniz C1700
Gottfried is a masculine German given name. It is derived from the Old High German name , recorded since the 7th century, and composed of the elements (conflated from the etyma for "God" and "good", and possibly further conflated with ) and ("peace" or "protection"). The German name was commonly hypocoristically abbreviated as '' Götz'' from the late medieval period. ''Götz'' and variants (including '' Göthe, Göthke'' and ''Göpfert'') also came into use as German surnames. Gottfried is also a common surname among Ashkenazi Jews. Given name The given name ''Gottfried'' became extremely frequent in Germany in the High Middle Ages, to the point of eclipsing most other names in ''God-'' (such as ''Godabert, Gotahard, Godohelm, Godomar, Goduin, Gotrat, Godulf'', etc.) The name was Latinised as ''Godefridus''. Medieval bearers of the name include: * Gotfrid, Duke of Alemannia and Raetia (d. 709) *Godefrid (d. c. 720), son of Drogo of Champagne, Frankish nobleman. *Godfrid H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Forms
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics. For instance, the expression f(x) \, dx is an example of a 1-form, -form, and can be integral, integrated over an interval [a,b] contained in the domain of f: \int_a^b f(x)\,dx. Similarly, the expression f(x,y,z) \, dx \wedge dy + g(x,y,z) \, dz \wedge dx + h(x,y,z) \, dy \wedge dz is a -form that can be integrated over a Surface (mathematics), surface S: \int_S \left(f(x,y,z) \, dx \wedge dy + g(x,y,z) \, dz \wedge dx + h(x,y,z) \, dy \wedge dz\right). The symbol \wedge denotes the exterior product, sometimes called the ''wedge product'', of two differential forms. Likewise, a -form f(x,y,z) \, dx \wedge dy \wedge dz represents a volume element that can be integrated over a region of space. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent And Independent Variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function (mathematics), function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Of Variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary differential equation, ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation. Ordinary differential equations (ODE) A differential equation for the unknown f(x) is separable if it can be written in the form :\frac f(x) = g(x)h(f(x)) where g and h are given functions. This is perhaps more transparent when written using y = f(x) as: :\frac=g(x)h(y). So now as long as ''h''(''y'') ≠ 0, we can rearrange terms to obtain: : = g(x) \, dx, where the two variables ''x'' and ''y'' have been separated. Note ''dx'' (and ''dy'') can be viewed, at a simple level, as just a convenient notation, which provides a handy mnemonic aid for assisting with manipulations. A formal definition of ''dx'' as a differential (infinitesimal) is somewhat advanced. Al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nova Methodus Pro Maximis Et Minimis
"Nova Methodus pro Maximis et Minimis" is the first published work on the subject of calculus. It was published by Gottfried Leibniz in the ''Acta Eruditorum'' in October 1684. It is considered to be the birth of infinitesimal calculus. Full title The full title of the published work is "Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus." In English, the full title can be translated as "A new method for maxima and minima, and for tangents, that is not hindered by fractional or irrational quantities, and a singular kind of calculus for the above mentioned." It is from this title that this branch of mathematics takes the name calculus. Influence Although calculus was independently co-invented by Isaac Newton Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scienti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Association Of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university A university () is an educational institution, institution of tertiary education and research which awards academic degrees in several Discipline (academia), academic disciplines. ''University'' is derived from the Latin phrase , which roughly ..., college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists; statisticians; and many others in academia, government, business, and industry. The MAA was founded in 1915 and is headquartered at 11 Dupont in the Dupont Circle, Washington, D.C., Dupont Circle neighborhood of Washington, D.C. The organization publishes mathematics journals and books, including the ''American Mathematical Monthly'' (established in 1894 by Benjamin Finkel), the most widely read mathematics journal in the world according to re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acta Eruditorum
(from Latin: ''Acts of the Erudite'') was the first scientific journal of the German-speaking lands of Europe, published from 1682 to 1782. History ''Acta Eruditorum'' was founded in 1682 in Leipzig by Otto Mencke, who became its first editor, with support from Gottfried Leibniz in Hanover, who contributed 13 articles over the journal's first four years. It was published by Johann Friedrich Gleditsch, with sponsorship from the Duke of Saxony, and was patterned after the French '' Journal des savants'' and the Italian ''Giornale de'letterati''. The journal was published monthly, entirely in Latin, and contained excerpts from new writings, reviews, small essays and notes. Most of the articles were devoted to the natural sciences and mathematics, including contributions (apart from Leibniz) from, e.g., Jakob Bernoulli, Humphry Ditton, Leonhard Euler, Ehrenfried Walther von Tschirnhaus, Pierre-Simon Laplace and Jérôme Lalande, but also from humanists and philosophers s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Sign
The integral symbol (''see below'') is used to denote integrals and antiderivatives in mathematics, especially in calculus. History The notation was introduced by the German mathematician Gottfried Wilhelm Leibniz in 1675 in his private writings; it first appeared publicly in the article "" (On a hidden geometry and analysis of indivisibles and infinites), published in ''Acta Eruditorum'' in June 1686. The symbol was based on the ſ (long s) character and was chosen because Leibniz thought of the integral as an infinite sum of infinitesimal summands. Typography in Unicode and LaTeX Fundamental symbol The integral symbol is in Unicode and \int in LaTeX. In HTML, it is written as ∫ (hexadecimal), ∫ (decimal) and ∫ ( named entity). The original IBM PC code page 437 character set included a couple of characters ⌠,⎮ and ⌡ (codes 244 and 245 respectively) to build the integral symbol. These were deprecated in subsequent MS-DOS code ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long S
The long s, , also known as the medial ''s'' or initial ''s'', is an Archaism, archaic form of the lowercase letter , found mostly in works from the late 8th to early 19th centuries. It replaced one or both of the letters ''s'' in a double-''s'' sequence (e.g., "ſinfulneſs" for "sinfulness" and "poſſeſs" or "poſseſs" for "possess", but never "poſſeſſ"). The modern letterform is known as the "short", "terminal", or "round" ''s''. In typography, the long ''s'' is known as a type of swash letter, commonly referred to as a "swash ''s''". The long ''s'' is the basis of the first half of the grapheme of the German alphabet Orthographic ligature, ligature letter , ( or , 'sharp ''s'''). As with other letters, the long ''s'' may have a variant appearance depending on typeface: , , , . Rules English This list of rules for the long ''s'' is not exhaustive, and it applies only to books printed during the 17th to early 19th centuries in English-speaking countries. Similar r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Symbol
The integral symbol (''see below'') is used to denote integrals and Antiderivative, antiderivatives in mathematics, especially in calculus. History The notation was introduced by the Germany, German mathematician Gottfried Wilhelm Leibniz in 1675 in his private writings; it first appeared publicly in the article "" (On a hidden geometry and analysis of indivisibles and infinites), published in ''Acta Eruditorum'' in June 1686. The symbol was based on the ſ (long s) character and was chosen because Leibniz thought of the integral as an infinite summation, sum of infinitesimal summands. Typography in Unicode and LaTeX Fundamental symbol The integral symbol is in Unicode and \int in LaTeX. In HTML, it is written as ∫ (hexadecimal), ∫ (decimal) and ∫ (List of XML and HTML character entity references#Character entity references in HTML, named entity). The original IBM PC code page 437 character set included a couple of characters ⌠,⎮ an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |