|
Laue Equations
In crystallography and solid state physics, the Laue equations relate incoming waves to outgoing waves in the process of elastic scattering, where the photon energy or light temporal frequency does not change upon scattering by a crystal lattice. They are named after physicist Max von Laue (1879–1960). The Laue equations can be written as \mathbf= \mathbf_ - \mathbf_ = \mathbf as the condition of elastic wave scattering by a crystal lattice, where \mathbf is the scattering vector, \mathbf_, \mathbf k_ are incoming and outgoing ''wave vectors'' (to the crystal and from the crystal, by scattering), and \mathbf is a crystal ''reciprocal lattice vector''. Due to elastic scattering , \mathbf_, ^2=, \mathbf_, ^2, three vectors. \mathbf, \mathbf_, and -\mathbf_ , form a rhombus if the equation is satisfied. If the scattering satisfies this equation, all the crystal lattice points scatter the incoming wave toward the scattering direction (the direction along \mathbf k_). If the equatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
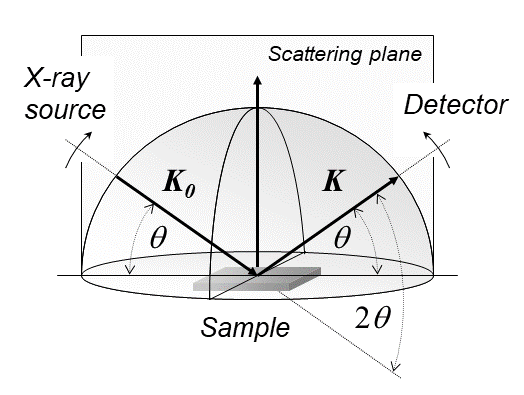
Laue Diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms. This article provides an overview of X-ray diffraction, starting with the early history of x-rays and the discovery that they have the right spacings to be diffracted by crystals. In many cases these diffraction patterns can be Interpreted using a single scattering or kinematical theory with conservation of energy (wave vector). Many different types of X-ray sources exist, ranging from ones u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Miller Index
Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices. In particular, a family of lattice planes of a given (direct) Bravais lattice is determined by three integers ''h'', ''k'', and ''ℓ'', the ''Miller indices''. They are written (''hkℓ''), and denote the family of (parallel) lattice planes (of the given Bravais lattice) orthogonal to \mathbf_ = h\mathbf_1 + k\mathbf_2 + \ell\mathbf_3 , where \mathbf_i are the basis or primitive translation vectors of the reciprocal lattice for the given Bravais lattice. (Note that the plane is not always orthogonal to the linear combination of direct or original lattice vectors h\mathbf_1 + k\mathbf_2 + \ell\mathbf_3 because the direct lattice vectors need not be mutually orthogonal.) This is based on the fact that a reciprocal lattice vector \mathbf (the vector indicating a reciprocal lattice point from the reciprocal lattice origin) is the wavevector of a plane wave in the Fouri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefront
In physics, the wavefront of a time-varying ''wave field (physics), field'' is the set (locus (mathematics), locus) of all point (geometry), points having the same ''phase (waves), phase''. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined). Wavefronts usually move with time. For waves propagating in a dimension (mathematics), unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surface (mathematics), surfaces in a three-dimensional one. For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (geometry)
In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement. A Euclidean plane with a chosen Cartesian coordinate system is called a '' Cartesian plane''. The set \mathbb^2 of the ordered pairs of real numbers (the real coordinate plane), equipped with the dot product, is often called ''the'' Euclidean plane or ''standard Euclidean plane'', since every Euclidean plane is isomorphic to it. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can move no faster than the speed of light measured in vacuum. The photon belongs to the class of boson particles. As with other elementary particles, photons are best explained by quantum mechanics and exhibit wave–particle duality, their behavior featuring properties of both waves and particles. The modern photon concept originated during the first two decades of the 20th century with the work of Albert Einstein, who built upon the research of Max Planck. While Planck was trying to explain how matter and electromagnetic radiation could be in thermal equilibrium with one another, he proposed that the energy stored within a material object should be regarded as composed of an integer number of discrete, equal-sized parts. To explain the pho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and directions, each attached to a point on the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout three dimensional space, such as the wind, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point. The elements of differential and integral calculus extend naturally to vector fields. When a vector field represents force, the line integral of a vector field represents the work done by a force moving along a path, and under this interpretation conservation of energy is exhibited as a special case of the fundamental theorem of calculus. Vector fields can usefully be thought of as representing the velocit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical quantity (with units). In a physical context, scalar fields are required to be independent of the choice of reference frame. That is, any two observers using the same units will agree on the value of the scalar field at the same absolute point in space (or spacetime) regardless of their respective points of origin. Examples used in physics include the temperature distribution throughout space, the pressure distribution in a fluid, and spin-zero quantum fields, such as the Higgs field. These fields are the subject of scalar field theory. Definition Mathematically, a scalar field on a region ''U'' is a real or complex-valued function or distribution on ''U''. The region ''U'' may be a set in some Euclidean space, Minkowski spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar (mathematics)
A scalar is an element of a field which is used to define a ''vector space''. In linear algebra, real numbers or generally elements of a field are called scalars and relate to vectors in an associated vector space through the operation of scalar multiplication (defined in the vector space), in which a vector can be multiplied by a scalar in the defined way to produce another vector. Generally speaking, a vector space may be defined by using any field instead of real numbers (such as complex numbers). Then scalars of that vector space will be elements of the associated field (such as complex numbers). A scalar product operation – not to be confused with scalar multiplication – may be defined on a vector space, allowing two vectors to be multiplied in the defined way to produce a scalar. A vector space equipped with a scalar product is called an inner product space. A quantity described by multiple scalars, such as having both direction and magnitude, is called a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Vector
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Optics
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or '' superposition'', of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts (also called phasefronts) whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium. A curved phasefront may be synthesized from an infinite number of these "natural modes" i.e., from plane wave phasefronts oriented in different directions in space. When an expanding spherical wave is far from its sources, it is locally tangent to a planar phase front (a single plane wave out of the infinite spectrum), which is transverse to the radial direction of prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |