|
Langlands
Langlands is a traditional English surname stemming from Middle English. It refers to the land holdings of the original person so named, and literally means “long (or vast) lands”. It may refer to: People * Alex Langlands, British archaeologist and historian * Alan Langlands, vice chancellor of the University of Leeds * Anders Langlands, visual effects supervisor * Geoffrey Langlands (1917–2019), British army officer and educator * George Langlands (1886–1951), Scottish footballer * Graeme Langlands (1941–2018), Australian rugby player and coach * Langlands and Bell, English artists * Robert Langlands (born 1936), Canadian mathematician ** Langlands classification ** Langlands decomposition ** Langlands dual ** Langlands group ** Langlands program In mathematics, the Langlands program is a set of conjectures about connections between number theory, the theory of automorphic forms, and geometry. It was proposed by . It seeks to relate the structure of Galois group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Langlands
Robert Phelan Langlands, (; born October 6, 1936) is a Canadian mathematician. He is best known as the founder of the Langlands program, a vast web of conjectures and results connecting representation theory and automorphic forms to the study of Galois groups in number theory, for which he received the 2018 Abel Prize. He is emeritus professor and occupied Albert Einstein's office at the Institute for Advanced Study in Princeton, until 2020 when he retired. Early life and career Langlands was born in New Westminster, British Columbia, Canada, in 1936 to Robert Langlands and Kathleen J Phelan. He has two younger sisters (Mary b. 1938; Sally b. 1941). In 1945, his family moved to White Rock, near the US border, where his parents had a building supply and construction business. He graduated from Semiahmoo Secondary School and started enrolling at the University of British Columbia at the age of 16, receiving his undergraduate degree in mathematics in 1957; he continued at UBC t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
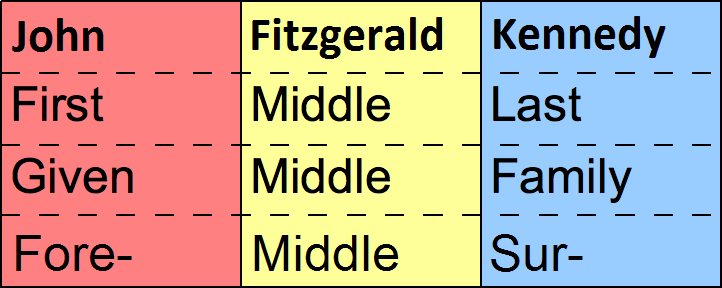
Surname
In many societies, a surname, family name, or last name is the mostly hereditary portion of one's personal name that indicates one's family. It is typically combined with a given name to form the full name of a person, although several given names and surnames are possible in the full name. In modern times most surnames are hereditary, although in most countries a person has a right to name change, change their name. Depending on culture, the surname may be placed either at the start of a person's name, or at the end. The number of surnames given to an individual also varies: in most cases it is just one, but in Portuguese-speaking countries and many Spanish-speaking countries, two surnames (one inherited from the mother and another from the father) are used for legal purposes. Depending on culture, not all members of a family unit are required to have identical surnames. In some countries, surnames are modified depending on gender and family membership status of a person. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands, Queensland
Langlands is a rural locality in the Western Downs Region, Queensland, Australia. In the , Langlands had a population of 30 people. Geography The locality is bounded loosely by Canaga Creek to the north, Canaga Creek Road to the west, Lower Jinghi Road to the south and Carlishs Road and Gadsbys Road to the east. The land is flat at above sea level. The predominant land use is crop growing. The Chinchilla–Wondai Road runs along the northern boundary. History Langlands State School opened on 18 April 1922. It closed on 29 January 1962. It was at 1033 Langlands Hall Road (). It was opposite the Langlands Hall (also called the East Canaga Hall) at (). Demographics In the , Langlands had a population of 7 people. In the , Langlands had a population of 30 people. Economy There are a number of homesteads in the locality: * Elouera () * Langlands () * Pleasant View () * Ponderosa () * Torquay () Education There are no schools in Langlands. The nearest primary schools ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Program
In mathematics, the Langlands program is a set of conjectures about connections between number theory, the theory of automorphic forms, and geometry. It was proposed by . It seeks to relate the structure of Galois groups in algebraic number theory to automorphic forms and, more generally, the representation theory of algebraic groups over local fields and adeles. It was described by Edward Frenkel as the " grand unified theory of mathematics." Background The Langlands program is built on existing ideas: the philosophy of cusp forms formulated a few years earlier by Harish-Chandra and , the work and Harish-Chandra's approach on semisimple Lie groups, and in technical terms the trace formula of Selberg and others. What was new in Langlands' work, besides technical depth, was the proposed connection to number theory, together with its rich organisational structure hypothesised (so-called functoriality). Harish-Chandra's work exploited the principle that what can be d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Group
In mathematics, the Langlands group is a conjectural group ''L''''F'' attached to each local or global field ''F'', that satisfies properties similar to those of the Weil group. It was given that name by Robert Kottwitz. In Kottwitz's formulation, the Langlands group should be an extension of the Weil group by a compact group. When ''F'' is local archimedean, ''LF'' is the Weil group of ''F'', when ''F'' is local non-archimedean, ''LF'' is the product of the Weil group of ''F'' with SU(2). When ''F'' is global, the existence of ''LF'' is still conjectural, though James Arthur gives a conjectural description of it. The Langlands correspondence for ''F'' is a "natural" correspondence between the irreducible ''n''-dimensional complex representations of ''LF'' and, in the global case, the cuspidal automorphic representations of GL''n''(A''F''), where A''F'' denotes the adele Adele Laurie Blue Adkins (; born 5 May 1988) is an English singer-songwriter. Regarded as a British cul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Dual
In representation theory, a branch of mathematics, the Langlands dual ''L''''G'' of a reductive algebraic group ''G'' (also called the ''L''-group of ''G'') is a group that controls the representation theory of ''G''. If ''G'' is defined over a field (mathematics), field ''k'', then ''L''''G'' is an extension of the absolute Galois group of ''k'' by a complex Lie group. There is also a variation called the Weil form of the ''L''-group, where the Galois group is replaced by a Weil group. Here, the letter ''L'' in the name also indicates the connection with the theory of L-functions, particularly the ''automorphic'' L-functions. The Langlands dual was introduced by in a letter to A. Weil. The ''L''-group is used heavily in the Langlands conjectures of Robert Langlands. It is used to make precise statements from ideas that automorphic forms are in a sense functorial in the group ''G'', when ''k'' is a global field. It is not exactly ''G'' with respect to which automorphic forms and r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup ''P'' of a semisimple Lie group as a product P=MAN of a reductive subgroup ''M'', an abelian subgroup ''A'', and a nilpotent subgroup ''N''. Applications A key application is in parabolic induction, which leads to the Langlands program In mathematics, the Langlands program is a set of conjectures about connections between number theory, the theory of automorphic forms, and geometry. It was proposed by . It seeks to relate the structure of Galois groups in algebraic number t ...: if G is a reductive algebraic group and P=MAN is the Langlands decomposition of a parabolic subgroup ''P'', then parabolic induction consists of taking a representation of MA, extending it to P by letting N act trivially, and inducing the result from P to G. See also * Lie group decompositions References Sources * A. W. Knapp, Structure theory of semisimple Lie groups. . Lie groups Algebraic groups {{Mathan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Classification
In mathematics, the Langlands classification is a description of the irreducible representations of a reductive Lie group ''G'', suggested by Robert Langlands (1973). There are two slightly different versions of the Langlands classification. One of these describes the irreducible Admissible representation, admissible (''g'', ''K'')-module (mathematics), modules, for ''g'' a Lie algebra of a reductive Lie group ''G'', with maximal compact subgroup ''K'', in terms of tempered representations of smaller groups. The tempered representations were in turn classified by Anthony W. Knapp, Anthony Knapp and Gregg Zuckerman. The other version of the Langlands classification divides the irreducible representations into L-packets, and classifies the L-packets in terms of certain homomorphisms of the Weil group of R or C into the Langlands dual group. Notation *''g'' is the Lie algebra of a real reductive Lie group ''G'' in the Harish-Chandra class. *''K'' is a maximal compact subgroup of ''G'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands And Bell
Langlands & Bell are two artists who work collaboratively. Ben Langlands (born London 1955) and Nikki Bell (born London 1959), began collaborating in 1978, while studying Fine Art at Middlesex Polytechnic in North London, from 1977 to 1980. Artistic practice and career Their artistic practice ranges from sculpture, film and video, to innovative digital media projects, art installations and full-scale architecture. Their work focuses on the complex web of relationships linking people with architecture and the built environment, and on a wider global level, the coded systems of mass-communications and exchange we use to negotiate an increasingly fast-changing technological world. Their first collaboration, in 1978, was an installation called ''The Kitchen'', consisting of two side-by-side kitchens, one created by Langlands and the other by Bell. In the mid-1980s, they became known for making monochromatic sculptures and reliefs, often in the form of furniture or architectural m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Middle English
Middle English (abbreviated to ME) is a form of the English language that was spoken after the Norman Conquest of 1066, until the late 15th century. The English language underwent distinct variations and developments following the Old English period. Scholarly opinion varies, but the University of Valencia states the period when Middle English was spoken as being from 1150 to 1500. This stage of the development of the English language roughly coincided with the High Middle Ages, High and Late Middle Ages. Middle English saw significant changes to its vocabulary, grammar, pronunciation, and orthography. Writing conventions during the Middle English period varied widely. Examples of writing from this period that have survived show extensive regional variation. The more standardized Old English literary variety broke down and writing in English became fragmented and localized and was, for the most part, being improvised. By the end of the period (about 1470), and aided by the movabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graeme Langlands
Graeme Frank Langlands, Member of the Most Excellent Order of the British Empire, MBE, (2 September 1941 – 20 January 2018), also known by the nickname of "Changa", was an Australian professional rugby league footballer who played from the 1950s till the 1970s and Coach (sport), coached in the 1970s. He retired as the most-capped player for the Australia national rugby league team, Australia national team with 45 international appearances from 1963 to 1975, and captained his country in 15 Test matches and Rugby League World Cup, World Cup games. Langlands was the and goal-kicker for the St. George Dragons in the latter half of their 11-year consecutive premiership-winning run from 1956 to 1966. Background Langlands was born on 2 September 1941 in Wollongong, New South Wales, Australia to Frank Horace Langlands and Hazel Miriam Ferguson. He had an unhappy childhood brought up by his alcoholic father. Playing career Langlands represented Combined NSW High Schools from 1955 to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Langlands
George Milne Langlands (1886–1951) was a Scottish footballer who played as an inside left for Dundee and Forfar Athletic. He was a member of the Dundee team that won the Scottish Cup in 1910 (in the first of three matches in the final, he scored the last-minute equaliser which forced a replay), having been runners-up in the Scottish Football League the previous season. In a career interrupted by World War I, he returned to hometown club Forfar Athletic (where he had also started out) after the conflict and was an important member of the team during the years when they moved up from the Scottish Football Alliance The Scottish Football Alliance was a league football structure set up in Scotland in competition with the Scottish Football League. Its success in the early years of professional football in both England and Scotland made the Alliance the basis for ... to become an SFL club. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |