|
Krippendorff's Alpha
Krippendorff's alpha coefficient, named after academic Klaus Krippendorff, is a statistical measure of the agreement achieved when coding a set of units of analysis. Since the 1970s, ''alpha'' has been used in content analysis where textual units are categorized by trained readers, in counseling and survey research where experts code open-ended interview data into analyzable terms, in psychological testing where alternative tests of the same phenomena need to be compared, or in observational studies where unstructured happenings are recorded for subsequent analysis. Krippendorff's alpha generalizes several known statistics, often called measures of inter-coder agreement, inter-rater reliability, reliability of coding given sets of units (as distinct from unitizing) but it also distinguishes itself from statistics that are called reliability coefficients but are unsuitable to the particulars of coding data generated for subsequent analysis. Krippendorff's alpha is applicable to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klaus Krippendorff
Klaus Krippendorff (March 21, 1932 – October 10, 2022) was a communication scholar, social science methodologist, and cyberneticist. and was the Gregory Bateson professor for Cybernetics, Language, and Culture at the University of Pennsylvania's Annenberg School for Communication. He wrote an influential textbook on content analysis and is the creator of the widely used and eponymous measure of interrater reliability, Krippendorff's alpha. In 1984–1985, he served as the president of the International Communication Association, one of the two largest professional associations for scholars of communication. Overview Krippendorff was born in 1932 in Frankfurt am Main in Germany. His father was an engineer at Junkers. In 1954, he graduated with an engineering degree from the State Engineering School Hannover (now Hanover University of Applied Sciences and Arts). In 1961, he graduated as diplom-designer from the Ulm School of Design (''Hochschule für Gestaltung Ulm''), Germa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spearman's Rank Correlation Coefficient
In statistics, Spearman's rank correlation coefficient or Spearman's ''ρ'' is a number ranging from -1 to 1 that indicates how strongly two sets of ranks are correlated. It could be used in a situation where one only has ranked data, such as a tally of gold, silver, and bronze medals. If a statistician wanted to know whether people who are high ranking in sprinting are also high ranking in long-distance running, they would use a Spearman rank correlation coefficient. The coefficient is named after Charles Spearman and often denoted by the Greek letter \rho (rho) or as r_s. It is a nonparametric measure of rank correlation ( statistical dependence between the rankings of two variables). It assesses how well the relationship between two variables can be described using a monotonic function. The Spearman correlation between two variables is equal to the Pearson correlation between the rank values of those two variables; while Pearson's correlation assesses linear relationshi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concordance Correlation Coefficient
In statistics, the concordance correlation coefficient measures the agreement between two variables, e.g., to evaluate reproducibility or for inter-rater reliability. Definition The form of the concordance correlation coefficient \rho_c as :\rho_c = \frac, where \mu_x and \mu_y are the means for the two variables and \sigma^2_x and \sigma^2_y are the corresponding variances. \rho is the Pearson's correlation coefficient between the two variables. This follows from its definition as :\rho_c = 1 - \frac . When the concordance correlation coefficient is computed on a N-length data set (i.e., N paired data values (x_n, y_n), for n=1,...,N), the form is :\hat_c = \frac, where the mean is computed as :\bar = \frac \sum_^N x_n and the variance :s_x^2 = \frac \sum_^N (x_n - \bar)^2 and the covariance :s_ = \frac \sum_^N (x_n - \bar)(y_n - \bar) . Whereas the ordinary correlation coefficient (Pearson's) is immune to whether the biased or unbiased versions for estimation of the variance i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goodman And Kruskal's Lambda
In probability theory and statistics, Goodman & Kruskal's lambda (\lambda) is a measure of proportional reduction in error in cross tabulation analysis. For any sample with a nominal independent variable and dependent variable (or ones that can be treated nominally), it indicates the extent to which the modal categories and frequencies for each value of the independent variable differ from the overall modal category and frequency, i.e., for all values of the independent variable together. \lambda is defined by the equation :\lambda = \frac. where :\varepsilon_1 is the overall non-modal frequency, and :\varepsilon_2 is the sum of the non-modal frequencies for each value of the independent variable. Values for lambda range from zero (no association between independent and dependent variables) to one ( perfect association). Weaknesses Although Goodman and Kruskal's lambda is a simple way to assess the association between variables, it yields a value of 0 (no association) wheneve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Psychometrika
''Psychometrika'' is the official journal of the Psychometric Society, a professional body dedicated to psychometrics and quantitative psychology. The journal focuses on quantitative methods for the measurement and evaluation of human behavior, including statistical methods and other mathematical techniques. Past editors include Marion Richardson, Dorothy Adkins, Norman Cliff, and Willem J. Heiser. According to ''Journal Citation Reports'', the journal had an impact factor of 2.9 in 2023. History In 1935, LL Thurstone, EL Thorndike and JP Guilford founded ''Psychometrika'' and also the Psychometric Society. Editors-in-chief The current editor of the journal is Sandip Sinharay of Educational Testing Service. The complete list of editor-in-chief of Psychometrika can be found at: https://www.psychometricsociety.org/content/past-psychometrika-editors The following is a subset of persons who have been editor-in-chief of Psychometrika: * Paul Horst * Albert K. Kurtz * Dorot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cronbach's Alpha
Cronbach's alpha (Cronbach's \alpha), also known as tau-equivalent reliability (\rho_T) or coefficient alpha (coefficient \alpha), is a reliability coefficient and a measure of the internal consistency of tests and measures. It was named after the American psychologist Lee Cronbach. Numerous studies warn against using Cronbach's alpha unconditionally. Statisticians regard reliability coefficients based on structural equation modeling (SEM) or generalizability theory as superior alternatives in many situations. History In his initial 1951 publication, Lee Cronbach described the coefficient as ''Coefficient'' ''alpha'' and included an additional derivation. ''Coefficient alpha'' had been used implicitly in previous studies, but his interpretation was thought to be more intuitively attractive relative to previous studies and it became quite popular. * In 1967, Melvin Novick and Charles Lewis proved that it was equal to reliability if the true scores of the compared tests ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cohen's Kappa
Cohen's kappa coefficient ('κ', lowercase Greek kappa) is a statistic that is used to measure inter-rater reliability (and also intra-rater reliability) for qualitative (categorical) items. It is generally thought to be a more robust measure than simple percent agreement calculation, as κ takes into account the possibility of the agreement occurring by chance. There is controversy surrounding Cohen's kappa due to the difficulty in interpreting indices of agreement. Some researchers have suggested that it is conceptually simpler to evaluate disagreement between items. History The first mention of a kappa-like statistic is attributed to Galton in 1892. The seminal paper introducing kappa as a new technique was published by Jacob Cohen (statistician), Jacob Cohen in the journal ''Educational and Psychological Measurement'' in 1960. Definition Cohen's kappa measures the agreement between two raters who each classify ''N'' items into ''C'' mutually exclusive categories. The definit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Association (statistics)
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
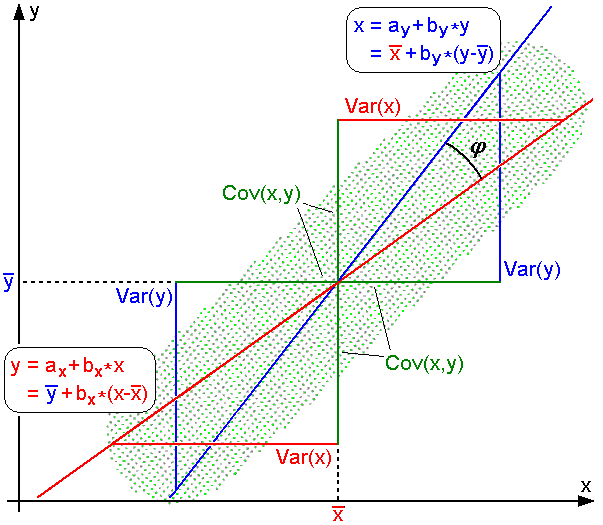
Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The namin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Level Of Measurement
Level of measurement or scale of measure is a classification that describes the nature of information within the values assigned to variables. Psychologist Stanley Smith Stevens developed the best-known classification with four levels, or scales, of measurement: nominal, ordinal, interval, and ratio. This framework of distinguishing levels of measurement originated in psychology and has since had a complex history, being adopted and extended in some disciplines and by some scholars, and criticized or rejected by others. Other classifications include those by Mosteller and Tukey, and by Chrisman. Stevens's typology Overview Stevens proposed his typology in a 1946 ''Science'' article titled "On the theory of scales of measurement". In that article, Stevens claimed that all measurement in science was conducted using four different types of scales that he called "nominal", "ordinal", "interval", and "ratio", unifying both " qualitative" (which are described by his "nominal" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a family of statistical methods used to compare the Mean, means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''within'' each group. If the between-group variation is substantially larger than the within-group variation, it suggests that the group means are likely different. This comparison is done using an F-test. The underlying principle of ANOVA is based on the law of total variance, which states that the total variance in a dataset can be broken down into components attributable to different sources. In the case of ANOVA, these sources are the variation between groups and the variation within groups. ANOVA was developed by the statistician Ronald Fisher. In its simplest form, it provides a statistical test of whether two or more population means are equal, and therefore generalizes the Student's t-test#Independent two-sample t-test, ''t''- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |