|
Kirchhoff–Love Plate Theory
The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by LoveA. E. H. Love, ''On the small free vibrations and deformations of elastic shells'', Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 p. 491–549. using assumptions proposed by Kirchhoff. The theory assumes that a mid-surface plane can be used to represent a three-dimensional plate in two-dimensional form. The following kinematic assumptions that are made in this theory:Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis. * straight lines normal to the mid-surface remain straight after deformation * straight lines normal to the mid-surface remain normal to the mid-surface after deformation * the thickness of the plate does not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plaque Mince Deplacement Element Matiere
Plaque may refer to: Commemorations or awards * Commemorative plaque, a plate, usually fixed to a wall or other vertical surface, meant to mark an event, person, etc. * Memorial Plaque (medallion), issued to next-of-kin of dead British military personnel after World War I * Plaquette, a small plaque in bronze or other materials Science and healthcare * Amyloid plaque * Atheroma or atheromatous plaque, a buildup of deposits within the wall of an artery * Dental plaque, a biofilm that builds up on teeth * A broad papule, a type of cutaneous condition * Pleural plaque, associated with mesothelioma, cancer often caused by exposure to asbestos * Senile plaques, an extracellular protein deposit in the brain implicated in Alzheimer's disease * Skin plaque, a plateau-like lesion that is greater in its diameter than in its depth * Viral plaque, a visible structure formed by virus propagation within a cell culture Other uses * Plaque, a rectangular casino token See also * * * Builder's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theodore Von Kármán
Theodore von Kármán ( , May 11, 1881May 6, 1963) was a Hungarian-American mathematician, aerospace engineer, and physicist who worked in aeronautics and astronautics. He was responsible for crucial advances in aerodynamics characterizing supersonic and hypersonic airflow. The human-defined threshold of outer space is named the " Kármán line" in recognition of his work. Kármán is regarded as an outstanding aerodynamic theoretician of the 20th century. Early life Theodore von Kármán was born into a Jewish family in Budapest, then part of Austria-Hungary, as Kármán Tódor, the son of Helene (Konn or Kohn, ) and . Among his ancestors were Rabbi Judah Loew ben Bezalel, who was said to be the creator of the Golem of Prague, and Rabbi , who wrote about Zohar. His father, Mór, was a well-known educator, who reformed the Hungarian school system and founded Minta Gymnasium in Budapest. He became an influential figure and became a commissioner of the Ministry of Educa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
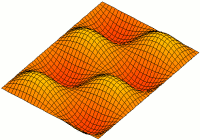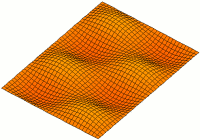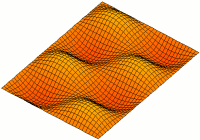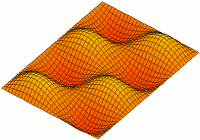
Vibration Of Plates
The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This permits a two-dimensional plate theory to give an excellent approximation to the actual three-dimensional motion of a plate-like object.Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis. There are several theories that have been developed to describe the motion of plates. The most commonly used are the Kirchhoff-Love theory and the Uflyand-Mindlin. The latter theory is discussed in detail by Elishakoff. Solutions to the governing equations predicted by these theories can give us insight into the behavior of plate-like objects both under free and forced conditions. This includes the propagation of waves and the study of standing waves and vibration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamilton's Principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action. It states that the dynamics of a physical system are determined by a variational problem for a functional based on a single function, the Lagrangian, which may contain all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the '' differential'' equations of motion of the physical system. Although formulated originally for classical mechanics, Hamilton's principle also applies to classical fields such as the electromagnetic and gravitational fields, and plays an important role in quantum mechanics, quantum field theory and criticality theories. Mathematical formulation Hamilton's principle states that the true evolution of a system described by generalized coordinates between two specified states and at two specified times and is a stationary point (a point where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Action (physics)
In physics, action is a scalar quantity that describes how the balance of kinetic versus potential energy of a physical system changes with trajectory. Action is significant because it is an input to the principle of stationary action, an approach to classical mechanics that is simpler for multiple objects. Action and the variational principle are used in Feynman's formulation of quantum mechanics and in general relativity. For systems with small values of action close to the Planck constant, quantum effects are significant. In the simple case of a single particle moving with a constant velocity (thereby undergoing uniform linear motion), the action is the momentum of the particle times the distance it moves, added up along its path; equivalently, action is the difference between the particle's kinetic energy and its potential energy, times the duration for which it has that amount of energy. More formally, action is a mathematical functional which takes the trajectory ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending Of Plates
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load. Bending of Kirchhoff-Love plates Definitions For a thin rectangular plate of thickness H, Young's modulus E, and Poisson's ratio \nu, we can define parameters in terms of the plate deflection, w. The flexural rigidity is given by : D = \frac Moments The bending moments per unit length are given by : M_ = -D \left( \frac + \nu \frac \right) : M_ = -D \left( \nu \frac + \frac \right) The twisting moment per unit length is given by : M_ = -D \left( 1 - \nu \right) \frac Forces The shear fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biharmonic Equation
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. Specifically, it is used in the modeling of thin structures that react Elasticity (physics), elastically to external forces. Notation It is written as \nabla^4 \varphi = 0 or \nabla^2 \nabla^2 \varphi = 0 or \Delta^2 \varphi = 0 where \nabla^4, which is the fourth power of the del operator and the square of the Laplacian operator \nabla^2 (or \Delta), is known as the biharmonic operator or the bilaplacian operator. In Cartesian coordinates, it can be written in n dimensions as: \nabla^4 \varphi = \sum_^n\sum_^n \partial_i\partial_i\partial_j\partial_j \varphi = \left(\sum_^n \partial_i\partial_i\right) \left(\sum_^n \partial_j\partial_j\right) \varphi. Because the formula here contains a summation of indices, many mathematicians prefer the notation \Delta^2 over \nabla^4 because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Bending
In solid mechanics Solid mechanics (also known as mechanics of solids) is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation (mechanics), deformation under the action of forces, temperature chang ..., pure bending (also known as the theory of simple bending) is a condition of Stress (mechanics), stress where a bending moment is applied to a Beam (structure), beam without the simultaneous presence of Cylinder stress, axial, Shear stress, shear, or Torsion (mechanics), torsional forces. Pure bending occurs only under a constant bending moment () since the shear force (), which is equal to \tfrac, has to be equal to zero. In reality, a state of pure bending does Idealization (philosophy of science), not practically exist, because such a state needs an absolutely weightless member. The state of pure bending is an approximation made to derive formulas. Kinematics of pure bending #In pure bending the axial lines ben ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus (or the Young modulus) is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress (force per unit area) applied to the object and the resulting axial strain (displacement or deformation) in the linear elastic region of the material. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first experiments that used the concept of Young's modulus in its modern form were performed by the Italian scientist Giordano Riccati in 1782, pre-dating Young's work by 25 years. The term modulus is derived from the Latin root term '' modus'', which means ''measure''. Definition Young's modulus, E, quantifies the relationship between tensile or compressive stress \sigma (force per unit ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson's Ratio
In materials science and solid mechanics, Poisson's ratio (symbol: ( nu)) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Poisson's ratio is the negative of the ratio of transverse strain to axial strain. For small values of these changes, is the amount of transversal elongation divided by the amount of axial compression. Most materials have Poisson's ratio values ranging between 0.0 and 0.5. For soft materials, such as rubber, where the bulk modulus is much higher than the shear modulus, Poisson's ratio is near 0.5. For open-cell polymer foams, Poisson's ratio is near zero, since the cells tend to collapse in compression. Many typical solids have Poisson's ratios in the range of 0.2 to 0.3. The ratio is named after the French mathematician and physicist Siméon Poisson. Origin Poisson's ratio is a measure of the Poisson effect, the phenomenon in whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plaque Moment Torsion Contrainte New
Plaque may refer to: Commemorations or awards * Commemorative plaque, a plate, usually fixed to a wall or other vertical surface, meant to mark an event, person, etc. * Memorial Plaque (medallion), issued to next-of-kin of dead British military personnel after World War I * Plaquette, a small plaque in bronze or other materials Science and healthcare * Amyloid plaque * Atheroma or atheromatous plaque, a buildup of deposits within the wall of an artery * Dental plaque, a biofilm that builds up on teeth * A broad papule, a type of cutaneous condition * Pleural plaque, associated with mesothelioma, cancer often caused by exposure to asbestos * Senile plaques, an extracellular protein deposit in the brain implicated in Alzheimer's disease * Skin plaque, a plateau-like lesion that is greater in its diameter than in its depth * Viral plaque, a visible structure formed by virus propagation within a cell culture Other uses * Plaque, a rectangular casino token See also * * * Builder's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |