|
Kernel Adaptive Filter
In signal processing, a kernel adaptive filter is a type of nonlinear adaptive filter. An adaptive filter is a filter that adapts its transfer function to changes in signal properties over time by minimizing an error or loss function that characterizes how far the filter deviates from ideal behavior. The adaptation process is based on learning from a sequence of signal samples and is thus an online algorithm. A nonlinear adaptive filter is one in which the transfer function is nonlinear. Kernel adaptive filters implement a nonlinear transfer function using kernel methods. In these methods, the signal is mapped to a high-dimensional linear feature space and a nonlinear function is approximated as a sum over kernels, whose domain is the feature space. If this is done in a reproducing kernel Hilbert space, a kernel method can be a universal approximator for a nonlinear function. Kernel methods have the advantage of having convex loss functions, with no local minima, and of being only m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
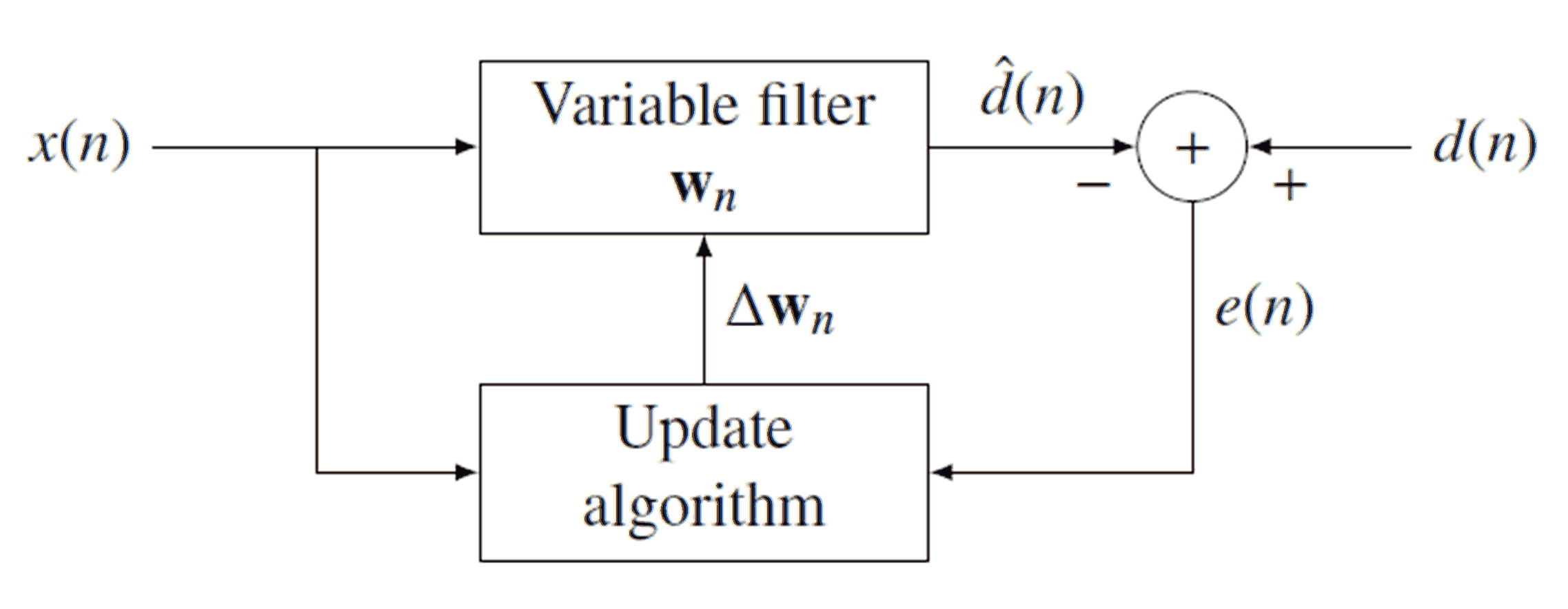
Adaptive Filter
An adaptive filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm. Because of the complexity of the optimization algorithms, almost all adaptive filters are digital filters. Adaptive filters are required for some applications because some parameters of the desired processing operation (for instance, the locations of reflective surfaces in a reverberant space) are not known in advance or are changing. The closed loop adaptive filter uses feedback in the form of an error signal to refine its transfer function. Generally speaking, the closed loop adaptive process involves the use of a cost function, which is a criterion for optimum performance of the filter, to feed an algorithm, which determines how to modify filter transfer function to minimize the cost on the next iteration. The most common cost function is the mean square of the error signal. As the pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible input. It is widely used in electronic engineering tools like Electronic circuit simulation, circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph (function), graph of an independent scalar (mathematics), scalar input versus the dependent scalar output (known as a transfer curve or characteristic curve). Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. Dimensions and units of the transfer function model the output response of the device for a range of possible inputs. The transfer function of a two-port electronic circuit, such as an amplifier, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
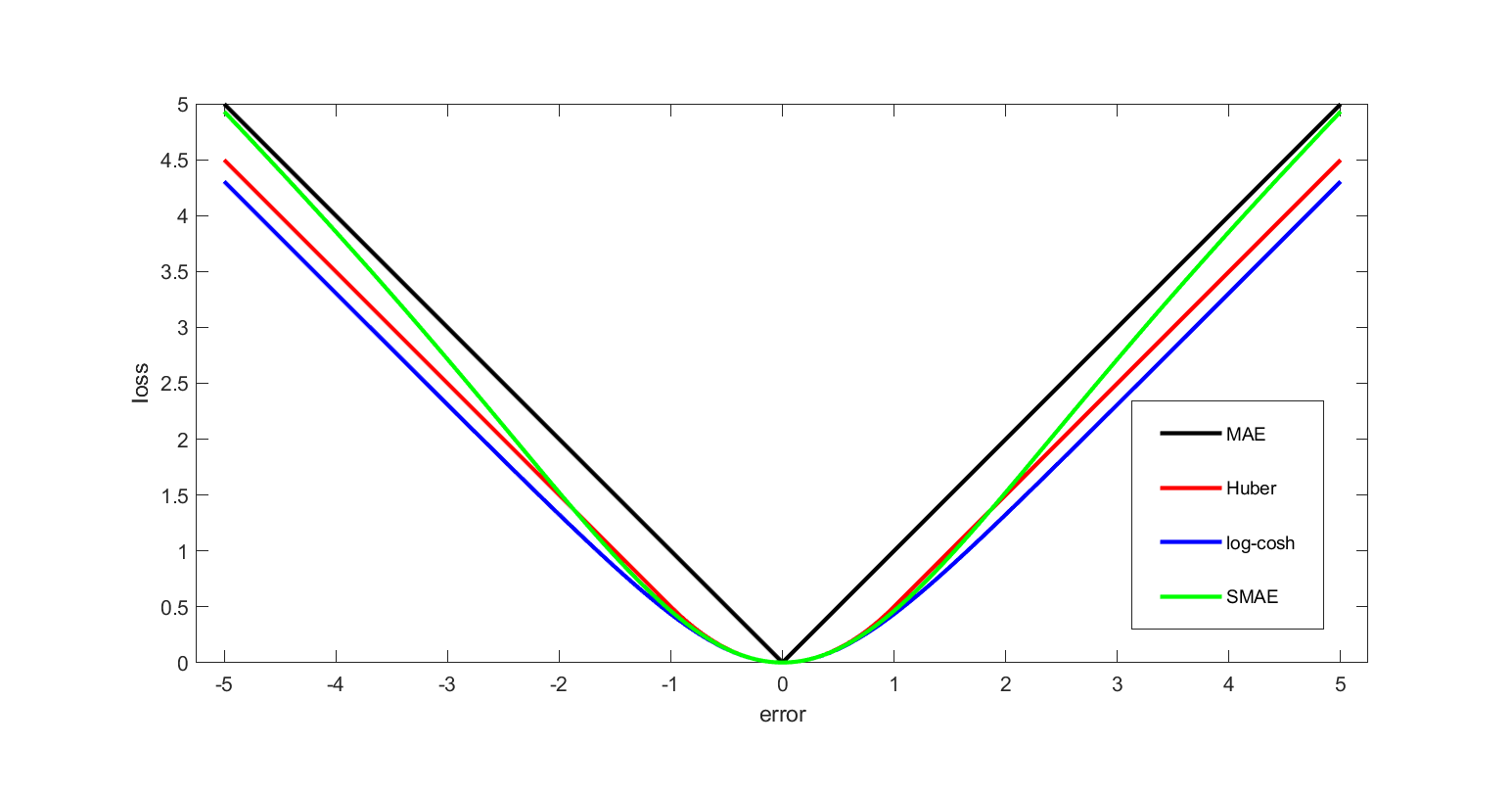
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Online Machine Learning
In computer science, online machine learning is a method of machine learning in which data becomes available in a sequential order and is used to update the best predictor for future data at each step, as opposed to batch learning techniques which generate the best predictor by learning on the entire training data set at once. Online learning is a common technique used in areas of machine learning where it is computationally infeasible to train over the entire dataset, requiring the need of out-of-core algorithms. It is also used in situations where it is necessary for the algorithm to dynamically adapt to new patterns in the data, or when the data itself is generated as a function of time, e.g., prediction of prices in the financial international markets. Online learning algorithms may be prone to catastrophic interference, a problem that can be addressed by incremental learning approaches. Introduction In the setting of supervised learning, a function of f : X \to Y is to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Methods
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). These methods involve using linear classifiers to solve nonlinear problems. The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feature (machine Learning)
In machine learning and pattern recognition, a feature is an individual measurable property or characteristic of a data set. Choosing informative, discriminating, and independent features is crucial to produce effective algorithms for pattern recognition, classification, and regression tasks. Features are usually numeric, but other types such as strings and graphs are used in syntactic pattern recognition, after some pre-processing step such as one-hot encoding. The concept of "features" is related to that of explanatory variables used in statistical techniques such as linear regression. Feature types In feature engineering, two types of features are commonly used: numerical and categorical. Numerical features are continuous values that can be measured on a scale. Examples of numerical features include age, height, weight, and income. Numerical features can be used in machine learning algorithms directly. Categorical features are discrete values that can be grouped into ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reproducing Kernel Hilbert Space
In functional analysis, a reproducing kernel Hilbert space (RKHS) is a Hilbert space of functions in which point evaluation is a continuous linear functional. Specifically, a Hilbert space H of functions from a set X (to \mathbb or \mathbb) is an RKHS if the point-evaluation functional L_x:H\to\mathbb, L_x(f)=f(x), is continuous for every x\in X. Equivalently, H is an RKHS if there exists a function K_x \in H such that, for all f \in H,\langle f, K_x \rangle = f(x).The function K_x is then called the ''reproducing kernel'', and it reproduces the value of f at x via the inner product. An immediate consequence of this property is that convergence in norm implies uniform convergence on any subset of X on which \, K_x\, is bounded. However, the converse does not necessarily hold. Often the set X carries a topology, and \, K_x\, depends continuously on x\in X, in which case: convergence in norm implies uniform convergence on compact subsets of X. It is not entirely straightforwar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of logic gate, gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Mean Squares Filter
Least mean squares (LMS) algorithms are a class of adaptive filter used to mimic a desired filter by finding the filter coefficients that relate to producing the least mean square of the error signal (difference between the desired and the actual signal). It is a stochastic gradient descent method in that the filter is only adapted based on the error at the current time. It was invented in 1960 by Stanford University professor Bernard Widrow and his first Ph.D. student, Ted Hoff, based on their research in single-layer neural networks ( ADALINE). Specifically, they used gradient descent to train ADALINE to recognize patterns, and called the algorithm "delta rule". They then applied the rule to filters, resulting in the LMS algorithm. Problem formulation The picture shows the various parts of the filter. x is the input signal, which is then transformed by an unknown filter h that we wish to match using \hat h. The output from the unknown filter is y, which is then interfered wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recursive Least Squares Filter
Recursive least squares (RLS) is an adaptive filter algorithm that recursively finds the coefficients that minimize a weighted linear least squares cost function relating to the input signals. This approach is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic, while for the LMS and similar algorithms they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity. Motivation RLS was discovered by Gauss but lay unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as :x(n)=\sum_^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Risk Minimization
Structural risk minimization (SRM) is an inductive principle of use in machine learning. Commonly in machine learning, a generalized model must be selected from a finite data set, with the consequent problem of overfitting – the model becoming too strongly tailored to the particularities of the training set and generalizing poorly to new data. The SRM principle addresses this problem by balancing the model's complexity against its success at fitting the training data. This principle was first set out in a 1974 book by Vladimir Vapnik and Alexey Chervonenkis and uses the VC dimension. In practical terms, Structural Risk Minimization is implemented by minimizing E_ + \beta H(W), where E_ is the train error, the function H(W) is called a regularization function, and \beta is a constant. H(W) is chosen such that it takes large values on parameters W that belong to high-capacity subsets of the parameter space. Minimizing H(W) in effect limits the capacity of the accessible subse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |