|
Kepler's Laws Of Planetary Motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in the heliocentric theory of Nicolaus Copernicus with elliptical orbits and explained how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law establishes that when a planet is closer to the Sun, it travels fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Laws Diagram
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer Astrology is a range of Divination, divinatory practices, recognized as pseudoscientific since the 18th century, that propose that information about human affairs and terrestrial events may be discerned by studying the apparent positions ..., Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his Kepler's laws of planetary motion, laws of planetary motion, and his books ''Astronomia nova'', ''Harmonice Mundi'', and ''Epitome Astronomiae Copernicanae'', influencing among others Isaac Newton, providing one of the foundations for his theory of Newton's law of universal gravitation, universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, Natural science, natural and modern science. He has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voltaire
François-Marie Arouet (; 21 November 169430 May 1778), known by his ''Pen name, nom de plume'' Voltaire (, ; ), was a French Age of Enlightenment, Enlightenment writer, philosopher (''philosophe''), satirist, and historian. Famous for his wit and his criticism of Christianity (especially Criticism of the Catholic Church, of the Roman Catholic Church) and of slavery, Voltaire was an advocate of freedom of speech, freedom of religion, and separation of church and state. Voltaire was a versatile and prolific writer, producing works in almost every literary form, including Stageplay, plays, poems, novels, essays, histories, and even scientific Exposition (narrative), expositions. He wrote more than 20,000 letters and 2,000 books and pamphlets. Voltaire was one of the first authors to become renowned and commercially successful internationally. He was an outspoken advocate of civil liberties and was at constant risk from the strict censorship laws of the Catholic French monarchy. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solstice
A solstice is the time when the Sun reaches its most northerly or southerly sun path, excursion relative to the celestial equator on the celestial sphere. Two solstices occur annually, around 20–22 June and 20–22 December. In many countries, the seasons of the year are defined by reference to the solstices and the equinoxes. The term ''solstice'' can also be used in a broader sense, as the day when this occurs. For locations not too close to the equator or the poles, the dates with the longest and shortest periods of daylight are the summer and winter solstices, respectively. Terms with no ambiguity as to which hemisphere is the context are "June solstice" and "December solstice", referring to the months in which they take place every year. Etymology The word ''solstice'' is derived from the Latin () and (), because at the solstices, the Sun's declination appears to "stand still"; that is, the seasonal movement of the Sun's sun path, daily path (as seen from Earth) paus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values. Apsides pertaining to orbits around different bodies have distinct names to differentiate themselves from other apsides. Apsides pertaining to geocentric orbits, orbits around the Earth, are at the farthest point called the ''apogee'', and at the nearest point the ''perigee'', like with orbits of satellites and the Moon around Earth. Apsides pertaining to orbits around the Sun are named ''aphelion'' for the farthest and ''perihelion'' for the nearest point in a heliocentric orbit. Earth's two apsides are the farthest point, ''aphelion'', and the nearest point, ''perihelion'', of its orbit around the host Sun. The terms ''aphelion'' and ''perihelion'' apply in the same way to the orbits of Jupiter and the other planets, the comets, and the asteroids of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
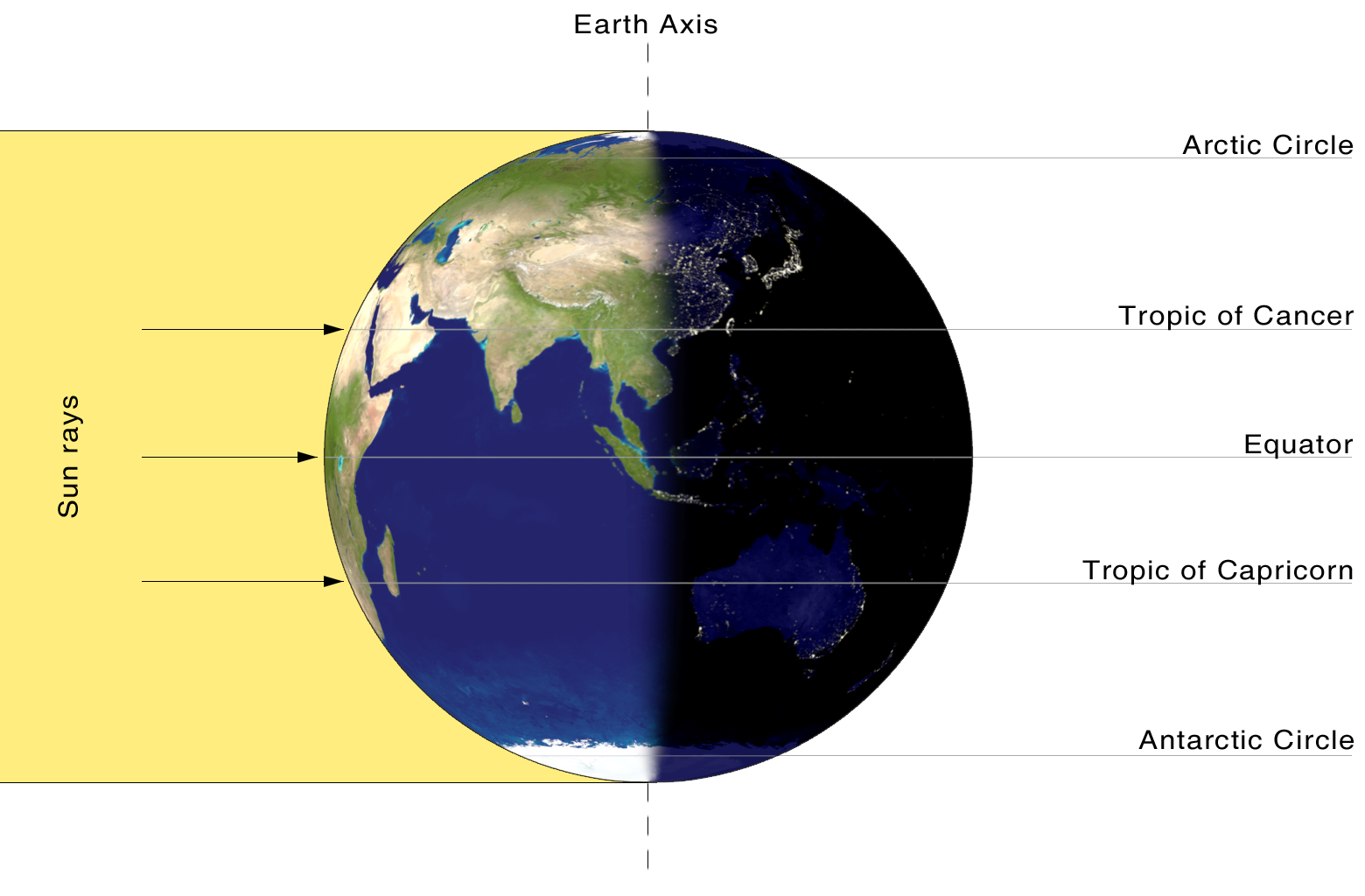
Equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumference, halfway between the North Pole, North and South Pole, South poles. The term can also be used for any other celestial body that is roughly spherical. In three-dimensional space, spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its geographical pole, poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane (geometry), plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
September Equinox
The September equinox (or southward equinox) is the moment when the Sun appears to cross the celestial equator, heading southward. Because of differences between the calendar year and the tropical year, the September equinox may occur from September 21 to 24. At the equinox, the Sun as viewed from the equator rises due east and sets due west. Before the Southward equinox, the Sun rises and sets more northerly, and afterwards, it rises and sets more southerly. The equinox may be taken to mark the end of astronomical summer and the beginning of astronomical autumn (autumnal equinox) in the Northern Hemisphere, while marking the end of astronomical winter and the start of astronomical spring (vernal equinox) in the Southern Hemisphere. Occurrences The September equinox is one point in time commonly used to determine the length of the tropical year. The dates and times of the September equinoxes that occur from the year 2018 to 2028 (UTC) are listed as follows: Const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
March Equinox
The March equinox or northward equinox is the equinox on the Earth when the subsolar point appears to leave the Southern Hemisphere and cross the celestial equator, heading northward as seen from Earth. The March equinox is known as the vernal equinox (or spring equinox) in the Northern Hemisphere and as the autumnal equinox (or fall equinox) in the Southern Hemisphere. On the Gregorian calendar at 0° longitude, the northward equinox can occur as early as 19 March (which happened most recently in 1796, and will happen next in 2044), and it can occur as late as 21 March (which happened most recently in 2007, and will happen next in 2102). For a common year the computed time slippage is about 5 hours 49 minutes ''later'' than the previous year, and for a leap year about 18 hours 11 minutes ''earlier'' than the previous year. Balancing the increases of the common years against the losses of the leap years keeps the calendar date of the March equinox from drifting more than ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit Of The Earth
Earth orbits the Sun at an astronomical unit, average distance of , or 8.317 light-second, light-minutes, in a retrograde and prograde motion, counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes days (1 sidereal year), during which time Earth has traveled .Jean Meeus, ''Astronomical Algorithms'' 2nd ed, (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough. Ignoring the influence of other Solar System bodies, Earth's orbit, also called Earth's revolution, is an ellipse with the Earth–Sun barycenter as one focus (geometry), focus with a current orbital eccentricity, eccentricity of 0.0167. Since this value is close to zero, the center of the orbit is relatively close to the center of the Sun (relative to the size of the orbit). As seen from Earth, the planet's orbital prograde motion makes the Sun diurnal motion, appear to move with respect to fixed stars, other star ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total angular momentum of a closed system remains constant. Angular momentum has both a direction (geometry), direction and a magnitude, and both are conserved. Bicycle and motorcycle dynamics, Bicycles and motorcycles, flying discs, Rifling, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Areal Velocity
In classical mechanics, areal velocity (also called sector velocity or sectorial velocity) is a pseudovector whose vector length, length equals the Rate of change (mathematics), rate of change at which area is swept out by a particle as it moves along a curve. It has SI units of square meters per second (m2/s) and dimension (physics), dimension of square length per time L2 T−1. In the adjoining figure, suppose that a particle moves along the blue curve. At a certain time ''t'', the particle is located at point ''B'', and a short while later, at time ''t'' + Δ''t'', the particle has moved to point ''C''. The region (mathematics), region swept out by the particle is shaded in green in the figure, bounded by the line segments ''AB'' and ''AC'' and the curve along which the particle moves. The areal velocity magnitude (i.e., the ''areal speed'') is this region's area divided by the time interval Δ''t'' in the limit that Δ''t'' becomes vanishingly small. The vector direction is po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |