|
Kempe's Universality Theorem
In 1876 Alfred B. Kempe published his article ''On a General Method of describing Plane Curves of the nth degree by Linkwork,'' which showed that for an arbitrary algebraic plane curve a linkage can be constructed that draws the curve. This direct connection between linkages and algebraic curves has been named Kempe's universality theorem that any bounded subset of an algebraic curve may be traced out by the motion of one of the joints in a suitably chosen linkage. Kempe's proof was flawed and the first complete proof was provided in 2002 based on his ideas. This theorem has been popularized by describing it as saying, "One can design a linkage which will sign your name!" Kempe recognized that his results demonstrate the existence of a drawing linkage but it would not be practical. He states It is hardly necessary to add, that this method would not be practically useful on account of the complexity of the linkwork employed, a necessary consequence of the perfect generality o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Kempe
Sir Alfred Bray Kempe FRS (6 July 1849 – 21 April 1922) was a mathematician best known for his work on linkages and the four colour theorem. Biography Kempe was the son of the Rector of St James's Church, Piccadilly, the Rev. John Edward Kempe. He was educated at St Paul's School, London and then studied at Trinity College, Cambridge, where Arthur Cayley was one of his teachers. He graduated BA (22nd wrangler) in 1872. Despite his interest in mathematics he became a barrister, specialising in the ecclesiastical law. He was knighted in 1913, the same year he became the Chancellor for the Diocese of London. He was also Chancellor of the dioceses of Newcastle, Southwell, St Albans, Peterborough, Chichester, and Chelmsford. He received the honorary degree DCL from the University of Durham and he was elected a Bencher of the Inner Temple in 1909. In 1876 he published his article ''On a General Method of describing Plane Curves of the nth degree by Linkwork,'' which presented ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linkage (mechanical)
A mechanical linkage is an assembly of systems connected to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain. Linkages may be constructed from open chains, closed chains, or a combination of open and closed chains. Each link in a chain is connected by a joint to one or more other links. Thus, a kinematic chain can be modeled as a graph in which the links are paths and the joints are vertices, which is called a linkage graph. The movement of an ideal joint is generally associated with a subgroup of the group of Euclidean displacements. The number of parameters in the subgroup is called the degrees of freedom (DOF) of the joint. Mechanical linkages are usually designed to trans ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curves
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential (mechanical Device)
A differential is a gear train with three drive shafts that has the property that the rotational speed of one shaft is the average of the speeds of the others, or a fixed multiple of that average. Functional description The following description of a differential applies to a traditional rear-wheel-drive car or truck with an open or limited slip differential combined with a reduction gearset using bevel gears (these are not strictly necessary; see spur-gear differential): Thus, for example, if the car is making a turn to the right, the main ring gear may make 10 full rotations. During that time, the left wheel will make more rotations because it has farther to travel, and the right wheel will make fewer rotations as it has less distance to travel. The sun gears (which drive the axle half-shafts) will rotate at different speeds relative to the ring gear (one faster, one slower) by, say, 2 full turns each (4 full turns relative to each other), resulting in the left wheel ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gear Train
A gear train is a mechanical system formed by mounting gears on a frame so the teeth of the gears engage. Gear teeth are designed to ensure the pitch circles of engaging gears roll on each other without slipping, providing a smooth transmission of rotation from one gear to the next. Features of gears and gear trains include: * The gear ratio of the pitch circles of mating gears defines the speed ratio and the mechanical advantage of the gear set. * A planetary gear train provides high gear reduction in a compact package. * It is possible to design gear teeth for gears that are non-circular, yet still transmit torque smoothly. * The speed ratios of chain and belt drives are computed in the same way as gear ratios. See bicycle gearing. The transmission of rotation between contacting toothed wheels can be traced back to the Antikythera mechanism of Greece and the south-pointing chariot of China. Illustrations by the Renaissance scientist Georgius Agricola show gear trains wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belt (mechanical)
A belt is a loop of flexible material used to link two or more rotating shafts mechanically, most often parallel. Belts may be used as a source of motion, to transmit power efficiently or to track relative movement. Belts are looped over pulleys and may have a twist between the pulleys, and the shafts need not be parallel. In a two pulley system, the belt can either drive the pulleys normally in one direction (the same if on parallel shafts), or the belt may be crossed, so that the direction of the driven shaft is reversed (the opposite direction to the driver if on parallel shafts). The belt drive can also be used to change the speed of rotation, either up or down, by using different sized pulleys. As a source of motion, a conveyor belt is one application where the belt is adapted to carry a load continuously between two points. History The mechanical belt drive, using a pulley machine, was first mentioned in the text the ''Dictionary of Local Expressions'' by the Han Dynas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Quaternion
In mathematics, the dual quaternions are an 8-dimensional real algebra isomorphic to the tensor product of the quaternions In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ... and the dual numbers. Thus, they may be constructed in the same way as the quaternions, except using dual numbers instead of real numbers as coefficients. A dual quaternion can be represented in the form , where ''A'' and ''B'' are ordinary quaternions and ε is the dual unit, which satisfies and commutes with every element of the algebra. Unlike quaternions, the dual quaternions do not form a division algebra. In mechanics, the dual quaternions are applied as a number system to represent rigid transformations in three dimensions. Since the space of dual quaternions is 8-dimensional and a rigid transforma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin(''nx'') and cos(''nx'') with ''n'' taking on the values of one or more natural numbers. The coefficients may be taken as real numbers, for real-valued functions. For complex coefficients, there is no difference between such a function and a finite Fourier series. Trigonometric polynomials are widely used, for example in trigonometric interpolation applied to the interpolation of periodic functions. They are used also in the discrete Fourier transform. The term ''trigonometric polynomial'' for the real-valued case can be seen as using the analogy: the functions sin(''nx'') and cos(''nx'') are similar to the monomial basis for polynomials. In the complex case the trigonometric polynomials are spanned by the positive and negative powers of ''e''''ix'', Laurent polynomials in ''z'' under the change of variables ''z'' = ''e''''i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. Properties If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & y (\theta) = (R - r) \sin \theta - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k - 1) \cos \theta + r \cos \left( (k - 1) \theta \right) \\ & y (\theta) = r (k - 1) \sin \theta - r \sin \left( (k - 1) \theta \right) \end If is an integer, then the curve is closed, and has cusps (i.e., sharp corners, where the curve is not differentiable). Specially for the curve is a straight line and the circles are called Cardano circles. Girolamo Car ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
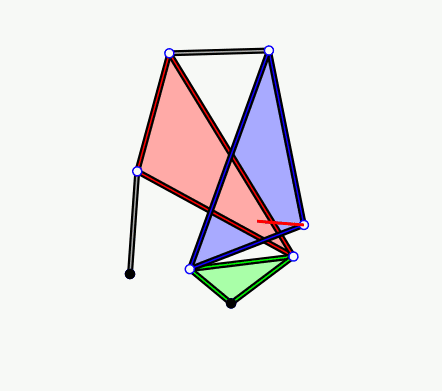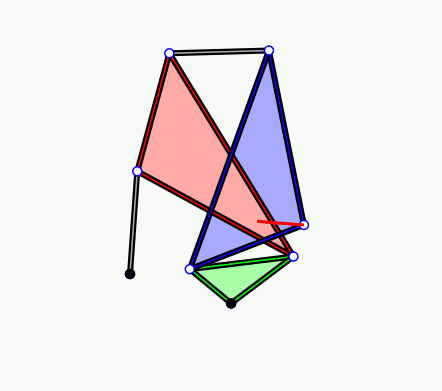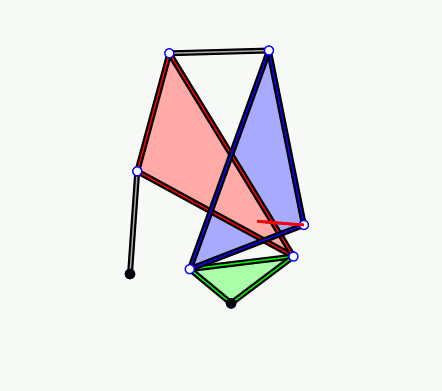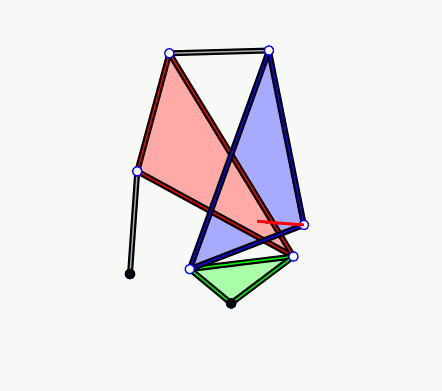
Single Coupled Serial Chain Trifolium Mechanism
Single may refer to: Arts, entertainment, and media * Single (music), a song release Songs * "Single" (Natasha Bedingfield song), 2004 * "Single" (New Kids on the Block and Ne-Yo song), 2008 * "Single" (William Wei song), 2016 * "Single", by Meghan Trainor from the album '' Only 17'' Sports * Single (baseball), the most common type of base hit * Single (cricket), point in cricket * Single (football), Canadian football point * Single-speed bicycle Transportation * Single-cylinder engine, an internal combustion engine design with one cylinder, or a motorcycle using such engine * Single (locomotive), a steam locomotive with a single pair of driving wheels * As a verb: to convert a double-track railway to a single-track railway Other uses * Single (mathematics) (1-tuple), a list or sequence with only one element * Single person, a person who is not in a committed relationship * Single precision, a computer numbering format that occupies one storage location in compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)



