|
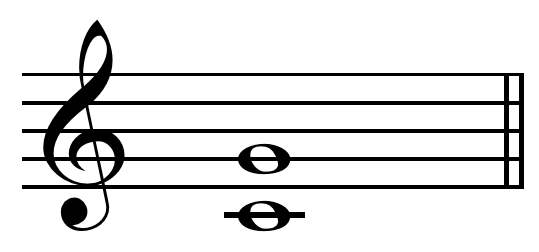
Just Intonation
In music, just intonation or pure intonation is a musical tuning, tuning system in which the space between notes' frequency, frequencies (called interval (music), intervals) is a natural number, whole number ratio, ratio. Intervals spaced in this way are said to be pure, and are called just intervals. Just intervals (and chords created by combining them) consist of tones from a single harmonic series (music), harmonic series of an implied fundamental frequency, fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth (music), fourth. In Western musical practice, bowed instruments such as violins, violas, cellos, and double basses are tuned using pure fifths or fourths. In contrast, keyboard instruments are rarely tuned using only pure intervals—the desire fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series Klang
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renaissance
The Renaissance ( , ) is a Periodization, period of history and a European cultural movement covering the 15th and 16th centuries. It marked the transition from the Middle Ages to modernity and was characterized by an effort to revive and surpass the ideas and achievements of classical antiquity. Associated with great social change in most fields and disciplines, including Renaissance art, art, Renaissance architecture, architecture, politics, Renaissance literature, literature, Renaissance exploration, exploration and Science in the Renaissance, science, the Renaissance was first centered in the Republic of Florence, then spread to the Italian Renaissance, rest of Italy and later throughout Europe. The term ''rinascita'' ("rebirth") first appeared in ''Lives of the Artists'' () by Giorgio Vasari, while the corresponding French word was adopted into English as the term for this period during the 1830s. The Renaissance's intellectual basis was founded in its version of Renaiss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Five-limit Tuning
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as . Powers of 2 represent intervallic movements by octaves. Powers of 3 represent movements by intervals of perfect fifths (plus one octave, which can be removed by multiplying by 1/2, i.e., 2−1). Powers of 5 represent intervals of major thirds (plus two octaves, removable by multiplying by 1/4, i.e., 2−2). Thus, 5-limit tunings are constructed entirely from stacking of three basic purely-tuned intervals (octaves, thirds and fifths). Since the perception of consonance seems related to low numbers in the harmonic series, and 5-limit tuning relies on the three lowest primes, 5-limit tuning should be capable of producing very conson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meantone Temperament
Meantone temperaments are musical temperaments; that is, a variety of Musical tuning#Tuning systems, tuning systems constructed, similarly to Pythagorean tuning, as a sequence of equal fifths, both rising and descending, scaled to remain within the same octave. But rather than using perfect fifths, consisting of frequency ratios of value 3:2, these are ''tempered'' by a suitable factor that narrows them to ratios that are slightly less than 3:2, in order to bring the major or minor thirds closer to Just intonation, the just intonation ratio of 5:4 or 6:5 , respectively. Among temperaments constructed as a sequence of fifths, a regular temperament is one in which all the fifths are chosen to be of the same size. Twelve-tone equal temperament () is obtained by making all semitones the same size, with each equal to one-twelfth of an octave; i.e. with ratios . Relative to Pythagorean tuning, it narrows the perfect fifths by about 2 cents (music), cents or of a Pythagorean co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Analysis
Musical analysis is the study of musical structure in either compositions or performances. According to music theorist Ian Bent, music analysis "is the means of answering directly the question 'How does it work?'". The method employed to answer this question, and indeed exactly what is meant by the question, differs from analyst to analyst, and according to the purpose of the analysis. According to Bent, "its emergence as an approach and method can be traced back to the 1750s. However it existed as a scholarly tool, albeit an auxiliary one, from the Middle Ages onwards." The principle of analysis has been variously criticized, especially by composers, such as Edgard Varèse's claim that, "to explain by means of nalysisis to decompose, to mutilate the spirit of a work". Analyses Some analysts, such as Donald Tovey (whose '' Essays in Musical Analysis'' are among the most accessible musical analyses) have presented their analyses in prose. Others, such as Hans Keller (who d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ninth
In music, a ninth is a compound interval consisting of an octave plus a second. Like the second, the interval of a ninth is classified as a dissonance in common practice tonality. Since a ninth is an octave larger than a second, its sonority level is considered less dense. Major ninth A major ninth is a compound musical interval spanning 14 semitones, or an octave plus 2 semitones. If transposed into a single octave, it becomes a major second or minor seventh. The major ninth is somewhat dissonant in sound. Transposition Some common transposing instruments sound a major ninth lower than written. These include the tenor saxophone, the bass clarinet, the baritone/euphonium when written in treble clef, and the trombone when written in treble clef ( British brass band music). When baritone/euphonium or trombone parts are written in bass clef or tenor clef they sound as written. Minor ninth A minor ninth (m9 or -9) is a compound musical interval spanning 13 semit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval from the first to the last of the first five consecutive Musical note, notes in a diatonic scale. The perfect fifth (often abbreviated P5) spans seven semitones, while the Tritone, diminished fifth spans six and the augmented fifth spans eight semitones. For example, the interval from C to G is a perfect fifth, as the note G lies seven semitones above C. The perfect fifth may be derived from the Harmonic series (music), harmonic series as the interval between the second and third harmonics. In a diatonic scale, the dominant (music), dominant note is a perfect fifth above the tonic (music), tonic note. The perfect fifth is more consonance and dissonance, consonant, or stable, than any other interval except the unison and the octave. It occu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are determined by choosing a sequence of fifthsBruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. which are " pure" or perfect, with ratio 3:2. This is chosen because it is the next harmonic of a vibrating string, after the octave (which is the ratio 2:1), and hence is the next most consonant "pure" interval, and the easiest to tune by ear. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈ 702 cents wide. The system dates back to Ancient Mesopotamia;. (See .) It is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (six ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Scale
The β (beta) scale is a non-octave-repeating musical scale invented by Wendy Carlos and first used on her album ''Beauty in the Beast'' (1986). It is derived from approximating just intervals using multiples of a single interval without, as is standard in equal temperaments, requiring an octave (2:1). It may be approximated by splitting the perfect fifth (3:2) into eleven equal parts 3:2) ≈ 63.8 cents It may be approximated by splitting the perfect fourth (4:3) into two equal parts 4:3)Milano, Dominic (November 1986)"A Many-Colored Jungle of Exotic Tunings" ''Keyboard''. or eight equal parts 4:3) = 64 centsCarlos, Wendy (2000/1986). "Liner notes", ''Beauty in the Beast''. ESD 81552. totaling approximately 18.8 steps per octave. The scale step may also precisely be derived from using 11:6 (B, 1049.36 cents, ) to approximate the interval , which equals 6:5 . \frac=0.05319411048 and 0.05319411048\times1200=63.832932576 () Although neither has an octave, one advantage to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alpha Scale
The (alpha) scale is a non-octave-repeating musical scale invented by Wendy Carlos and first used on her album ''Beauty in the Beast'' (1986). It is derived from approximating just intervals using multiples of a single interval, but without requiring (as temperaments normally do) an octave (2:1). It may be approximated by dividing the perfect fifth (3:2) into nine equal steps, with frequency ratio \ \left( \tfrac \right)^\ , or by dividing the minor third (6:5) into four frequency ratio steps of \ \left( \tfrac \right)^ ~. The size of this scale step may also be precisely derived from using 9:5 B, 1017.60 cents, to approximate the interval E, 315.64 cents, . : Carlos' (alpha) scale arises from ... taking a value for the scale degree so that nine of them approximate a 3:2 perfect fifth, five of them approximate a 5:4 major third, and four of them approximate a 6:5 minor third. In order to make the approximation as good as possible we minimize the mean s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wendy Carlos
Wendy Carlos (born Walter Carlos; November 14, 1939) is an American musician and composer known for electronic music and film scores. Born and raised in Rhode Island, Carlos studied physics and music at Brown University before moving to New York City in 1962 to study music composition at Columbia University. Studying and working with various electronic musicians and technicians at the city's Computer Music Center, Columbia-Princeton Electronic Music Center, she helped in the development of the Moog synthesizer, Robert Moog's first commercially available keyboard instrument. Carlos came to prominence with ''Switched-On Bach'' (1968), an album of music by Johann Sebastian Bach performed on a Moog synthesizer, which helped popularize its use in the 1970s and won her three Grammy Awards. Its commercial success led to several more albums, including further synthesized classical music adaptations, and experimental music, experimental and ambient music. She composed the score to two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (music)
In music theory, limits or harmonic limits are a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term ''limit'' was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name. The harmonic series and the evolution of music Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance). In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose ( contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |