|
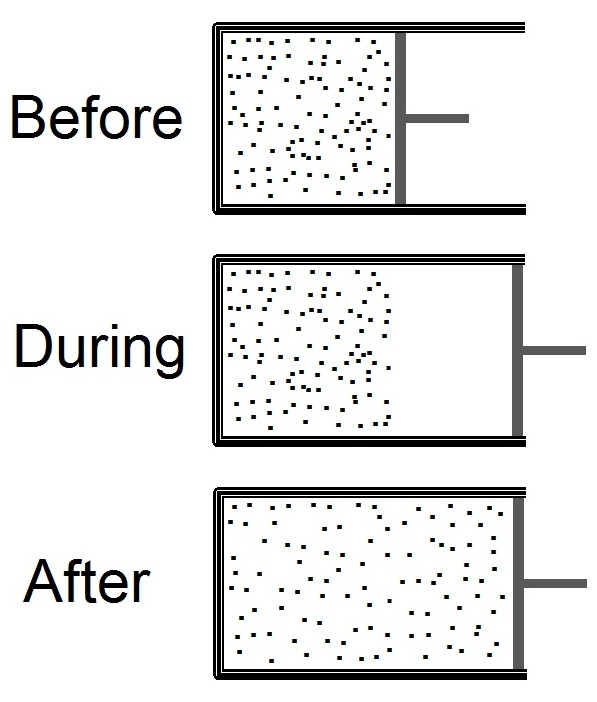
Joule Expansion
The Joule expansion (a subset of free expansion) is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container (via a small partition), with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container. The Joule expansion, treated as a thought experiment involving ideal gases, is a useful exercise in classical thermodynamics. It provides a convenient example for calculating changes in thermodynamic quantities, including the resulting increase in entropy of the universe (entropy production) that results from this inherently irreversible process. An actual Joule expansion experiment necessarily involves real gases; the temperature change in such a process provides a measure of intermolecular forces. This type of expansion is named after James Prescott Joule who used this expansion, in 1845, in his study for the mechanical e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic System
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics. Thermodynamic systems can be passive and active according to internal processes. According to internal processes, passive systems and active systems are distinguished: passive, in which there is a redistribution of available energy, active, in which one type of energy is converted into another. Depending on its interaction with the environment, a thermodynamic system may be an isolated system, a Closed system#In thermodynamics, closed system, or an Open system (systems theory), open system. An isolated system does not exchange matter or energy with its surroundings. A closed system may exchange heat, experience forces, and exert forces, but does not exchange matter. An open system can interact with its surroundings by exchanging both matter and energy. The physical condition of a thermodynamic system at a given time is described by its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Szilard's Engine
Because the mathematical expressions for information theory developed by Claude Shannon and Ralph Hartley in the 1940s are similar to the mathematics of statistical thermodynamics worked out by Ludwig Boltzmann and J. Willard Gibbs in the 1870s, in which the concept of entropy is central, Shannon was persuaded to employ the same term 'entropy' for his measure of uncertainty. Information entropy is often presumed to be equivalent to physical (thermodynamic) entropy. Equivalence of form of the defining expressions The defining expression for entropy in the theory of statistical mechanics established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s, is of the form: : S = - k_\text \sum_i p_i \ln p_i , where p_i is the probability of the microstate ''i'' taken from an equilibrium ensemble, and k_B is the Boltzmann constant. The defining expression for entropy in the theory of information established by Claude E. Shannon in 1948 is of the form: : H = - \sum_i p_i \log_b p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Expansion
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion and cooling of moist air, which can be triggered by w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Thermodynamic Relation
In thermodynamics, the fundamental thermodynamic relation are four fundamental equations which demonstrate how four important thermodynamic quantities depend on variables that can be controlled and measured experimentally. Thus, they are essentially equations of state, and using the fundamental equations, experimental data can be used to determine sought-after quantities like ''G'' (Gibbs free energy) or ''H'' (enthalpy). The relation is generally expressed as a microscopic change in internal energy in terms of microscopic changes in entropy, and volume for a closed system in thermal equilibrium in the following way. \mathrmU= T\,\mathrmS - P\,\mathrmV\, Here, ''U'' is internal energy, ''T'' is absolute temperature, ''S'' is entropy, ''P'' is pressure, and ''V'' is volume. This is only one expression of the fundamental thermodynamic relation. It may be expressed in other ways, using different variables (e.g. using thermodynamic potentials). For example, the fundamental relation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sackur–Tetrode Equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic ideal gas. It is named for Hugo Martin Tetrode (1895–1931) and Otto Sackur (1880–1914), who developed it independently as a solution of Boltzmann's gas statistics and entropy equations, at about the same time in 1912. Formula The Sackur–Tetrode equation expresses the entropy S of a monatomic ideal gas in terms of its thermodynamic state—specifically, its volume V, internal energy U, and the number of particles N: : \frac = \ln \left \frac VN \left(\frac\frac UN\right)^\right , where k_\mathrm is the Boltzmann constant, m is the mass of a gas particle and h is the Planck constant. The equation can also be expressed in terms of the thermal wavelength \Lambda: : \frac = \ln\left(\frac\right)+\frac , For a derivation of the Sackur–Tetrode equation, see the Gibbs paradox. For the constraints placed upon the entropy of an ideal gas by thermodynamics alone, see the ideal gas article. The abov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monatomic Gas
In physics and chemistry, "monatomic" is a combination of the words "mono" and "atomic", and means "single atom". It is usually applied to gases: a monatomic gas is a gas in which atoms are not bound to each other. Examples at standard conditions of temperature and pressure include all the noble gases (helium, neon, argon, krypton, xenon, and radon), though all chemical elements will be monatomic in the gas phase at sufficiently high temperature (or very low pressure). The thermodynamic behavior of a monatomic gas is much simpler when compared to polyatomic gases because it is free of any rotational or vibrational energy. Noble gases The only chemical elements that are stable single atoms (so they are not molecules) at standard temperature and pressure (STP) are the noble gases. These are helium, neon, argon, krypton, xenon, and radon. Noble gases have a full outer valence shell making them rather non-reactive species. While these elements have been described historically as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Process
An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an '' adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The noun '' isotherm'' is derived from the Ancient Greek words (), meaning "equal", and (), meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Of State
In the thermodynamics of equilibrium, a state function, function of state, or point function for a thermodynamic system is a mathematical function relating several state variables or state quantities (that describe equilibrium states of a system) that depend only on the current equilibrium thermodynamic state of the system (e.g. gas, liquid, solid, crystal, or emulsion), not the path which the system has taken to reach that state. A state function describes equilibrium states of a system, thus also describing the type of system. A state variable is typically a state function so the determination of other state variable values at an equilibrium state also determines the value of the state variable as the state function at that state. The ideal gas law is a good example. In this law, one state variable (e.g., pressure, volume, temperature, or the amount of substance in a gaseous equilibrium system) is a function of other state variables so is regarded as a state function. A state ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lennard-Jones Potential
In computational chemistry, molecular physics, and physical chemistry, the Lennard-Jones potential (also termed the LJ potential or 12-6 potential; named for John Lennard-Jones) is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential is often used as a building block in molecular models (a.k.a. force fields) for more complex substances. Many studies of the idealized "Lennard-Jones substance" use the potential to understand the physical nature of matter. Overview The Lennard-Jones potential is a simple model that still manages to describe the essential features of interactions between simple atoms and molecules: Two interacting particles repel each other at very close distance, attract each other at moderate distance, and eventually stop intera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Energy
The internal energy of a thermodynamic system is the energy of the system as a state function, measured as the quantity of energy necessary to bring the system from its standard internal state to its present internal state of interest, accounting for the gains and losses of energy due to changes in its internal state, including such quantities as magnetization. It excludes the kinetic energy of motion of the system as a whole and the potential energy of position of the system as a whole, with respect to its surroundings and external force fields. It includes the thermal energy, ''i.e.'', the constituent particles' kinetic energies of motion relative to the motion of the system as a whole. Without a thermodynamic process, the internal energy of an isolated system cannot change, as expressed in the law of conservation of energy, a foundation of the first law of thermodynamics. The notion has been introduced to describe the systems characterized by temperature variations, te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance. The Boltzmann constant and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |