|
Isomorphism (crystallography)
In chemistry, isomorphism has meanings both at the level of crystallography and at a molecular level. In crystallography, crystals are isomorphous if they have identical symmetry and if the atomic positions can be described with a set of parameters (unit cell dimensions and fractional coordinates) whose numerical values differ only slightly. Molecules are isomorphous if they have similar shapes. The coordination complexes tris(acetylacetonato)iron (Fe(acac)3) and tris(acetylacetonato)aluminium (Al(acac)3) are isomorphous. These compounds, both of ''D''3 symmetry have very similar shapes, as determined by bond lengths and bond angles. Isomorphous compounds give rise to isomorphous crystals and form solid solutions. Historically, crystal shape was defined by measuring the angles between crystal faces with a goniometer. Whereas crystals of Fe(acac)3 are deep red and crystals of Al(acac)3 are colorless, a solid solution of the two, i.e. Fe1−xAlx(acac)3 will be deep or pale pi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forsterite
Forsterite (Mg2SiO4; commonly abbreviated as Fo; also known as white olivine) is the magnesium-rich Endmember, end-member of the olivine solid solution series. It is Isomorphism (crystallography), isomorphous with the iron-rich end-member, fayalite. Forsterite crystallizes in the orthorhombic system (space group ''Pbnm'') with cell parameters ''a'' 4.75 Ångström, Å (0.475 Nanometre, nm), ''b'' 10.20 Å (1.020 nm) and ''c'' 5.98 Å (0.598 nm). Forsterite is associated with Igneous rock, igneous and metamorphic rocks and has also been found in meteorites. In 2005 it was also found in cometary dust returned by the Stardust probe. In 2011 it was observed as tiny crystals in the dusty clouds of gas around a forming star. Two Polymorphism (materials science), polymorphs of forsterite are known: wadsleyite (also orthorhombic) and ringwoodite (isometric, cubic crystal system). Both are mainly known from meteorites. Peridot is the gemstone variety of forsterite olivine. Comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zinc
Zinc is a chemical element; it has symbol Zn and atomic number 30. It is a slightly brittle metal at room temperature and has a shiny-greyish appearance when oxidation is removed. It is the first element in group 12 (IIB) of the periodic table. In some respects, zinc is chemically similar to magnesium: both elements exhibit only one normal oxidation state (+2), and the Zn2+ and Mg2+ ions are of similar size. Zinc is the 24th most abundant element in Earth's crust and has five stable isotopes. The most common zinc ore is sphalerite (zinc blende), a zinc sulfide mineral. The largest workable lodes are in Australia, Asia, and the United States. Zinc is refined by froth flotation of the ore, roasting, and final extraction using electricity ( electrowinning). Zinc is an essential trace element for humans, animals, plants and for microorganisms and is necessary for prenatal and postnatal development. It is the second most abundant trace metal in humans after iron, an import ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Goldschmidt Tolerance Factor
Goldschmidt's tolerance factor (from the German word ''Toleranzfaktor'') is an indicator for the stability and distortion of crystal structures. It was originally only used to describe the perovskite ABO3 structure, but now tolerance factors are also used for ilmenite. Alternatively the tolerance factor can be used to calculate the compatibility of an ion with a crystal structure. The first description of the tolerance factor for perovskite was made by Victor Moritz Goldschmidt in 1926. Mathematical expression The Goldschmidt tolerance factor (t) is a dimensionless number that is calculated from the ratio of the ionic radii: In an ideal cubic perovskite structure, the lattice parameter (i.e., length) of the unit cell (a) can be calculated using the following equation: Perovskite structure The perovskite structure has the following tolerance factors (t): See also * Goldschmidt classification * Victor Goldschmidt Victor Moritz Goldschmidt (27 January 1888 – ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polymorphism (materials Science)
In crystallography, polymorphism is the phenomenon where a compound or element can crystallize into more than one crystal structure. The preceding definition has evolved over many years and is still under discussion today. Discussion of the defining characteristics of polymorphism involves distinguishing among types of transitions and structural changes occurring in polymorphism versus those in other phenomena. Overview Phase transitions (phase changes) that help describe polymorphism include polymorphic transitions as well as melting and vaporization transitions. According to IUPAC, a polymorphic transition is "A reversible transition of a solid crystalline phase at a certain temperature and pressure (the inversion point) to another phase of the same chemical composition with a different crystal structure." Additionally, Walter McCrone described the phases in polymorphic matter as "different in crystal structure but identical in the liquid or vapor states." McCrone also def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asterism (gemology)
An asterism () is a star-shaped concentration of light reflected or refracted from a gemstone. It can appear when a suitable stone is cut ''en cabochon'' (i.e. shaped and polished, not faceted). A gemstone that exhibits this effect is called a star stone or asteria. The best known is star sapphire, but many other minerals can also be asteria, usually due to impurities in the crystal structure. Archetype The archetypal asteria is the star sapphire, generally corundum with near uniform impurities which is bluish-grey and milky or opalescent, which when lit has a star of six rays. In the red instance stellate reflection is rarer; the star-ruby occasionally found with the star-sapphire in Sri Lanka is among the most valued of "fancy stones". Other examples are star-topaz (8 rays) and star diopside (4 rays); star garnets may display four-rayed or six-rayed asterisms. Description Asterism is generated by reflections of light from twin-lamellae or from extremely fine needle-shap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ferenc Szabadváry
Ferenc Szabadváry (1 September 1923 – 21 May 2006) was a Hungarians, Hungarian chemist and historian. From 1971 he was director at the Hungarian National Museum for Science and Technology. In 1960 he published a history of analytical chemistry in Hungarian. A translation was made by Gyula Svehla in 1966, first published with Pergamon Press and later Gordon and Breach. Szabadváry received the Dexter Award in 1970. References 1923 births 2006 deaths Hungarian chemists Historians of chemistry 20th-century Hungarian historians {{Hungary-scientist-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eilhard Mitscherlich
Eilhard Mitscherlich (; 7 January 179428 August 1863) was a German chemist, who is perhaps best remembered today for his discovery of the phenomenon of crystallographic isomorphism in 1819. Early life and work Mitscherlich was born at Neuende (now a part of Wilhelmshaven) in the Lordship of Jever, where his father was pastor. His uncle, Christoph Wilhelm Mitscherlich (1760–1854), professor at the University of Göttingen, was in his day a celebrated scholar. Eilhard Mitscherlich was educated at Jever by the historian Friedrich Christoph Schlosser, and in 1811 went to the University of Heidelberg devoting himself to philology, with an emphasis on the Persian language. In 1813 he went to Paris to seek permission to join the embassy which Napoleon I of France was establishing in Persia. The abdication of Napoleon Bonaparte in 1814 put an end to this, and Mitscherlich resolved to study medicine in order that he might enjoy that freedom of travel usually allowed in the East to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Germans
Germans (, ) are the natives or inhabitants of Germany, or sometimes more broadly any people who are of German descent or native speakers of the German language. The Basic Law for the Federal Republic of Germany, constitution of Germany, implemented in 1949 following the end of World War II, defines a German as a German nationality law, German citizen. During the 19th and much of the 20th century, discussions on German identity were dominated by concepts of a common language, culture, descent, and history.. "German identity developed through a long historical process that led, in the late 19th and early 20th centuries, to the definition of the German nation as both a community of descent (Volksgemeinschaft) and shared culture and experience. Today, the German language is the primary though not exclusive criterion of German identity." Today, the German language is widely seen as the primary, though not exclusive, criterion of German identity. Estimates on the total number of Germ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scientific Law
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. The term ''law'' has diverse usage in many cases (approximate, accurate, broad, or narrow) across all fields of natural science (physics, chemistry, astronomy, geoscience, biology). Laws are developed from data and can be further developed through mathematics; in all cases they are directly or indirectly based on empirical evidence. It is generally understood that they implicitly reflect, though they do not explicitly assert, causal relationships fundamental to reality, and are discovered rather than invented. Scientific laws summarize the results of experiments or observations, usually within a certain range of application. In general, the accuracy of a law does not change when a new theory of the relevant phenomenon is worked out, but rather the scope of the law's application, since the mathematics or statement representin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
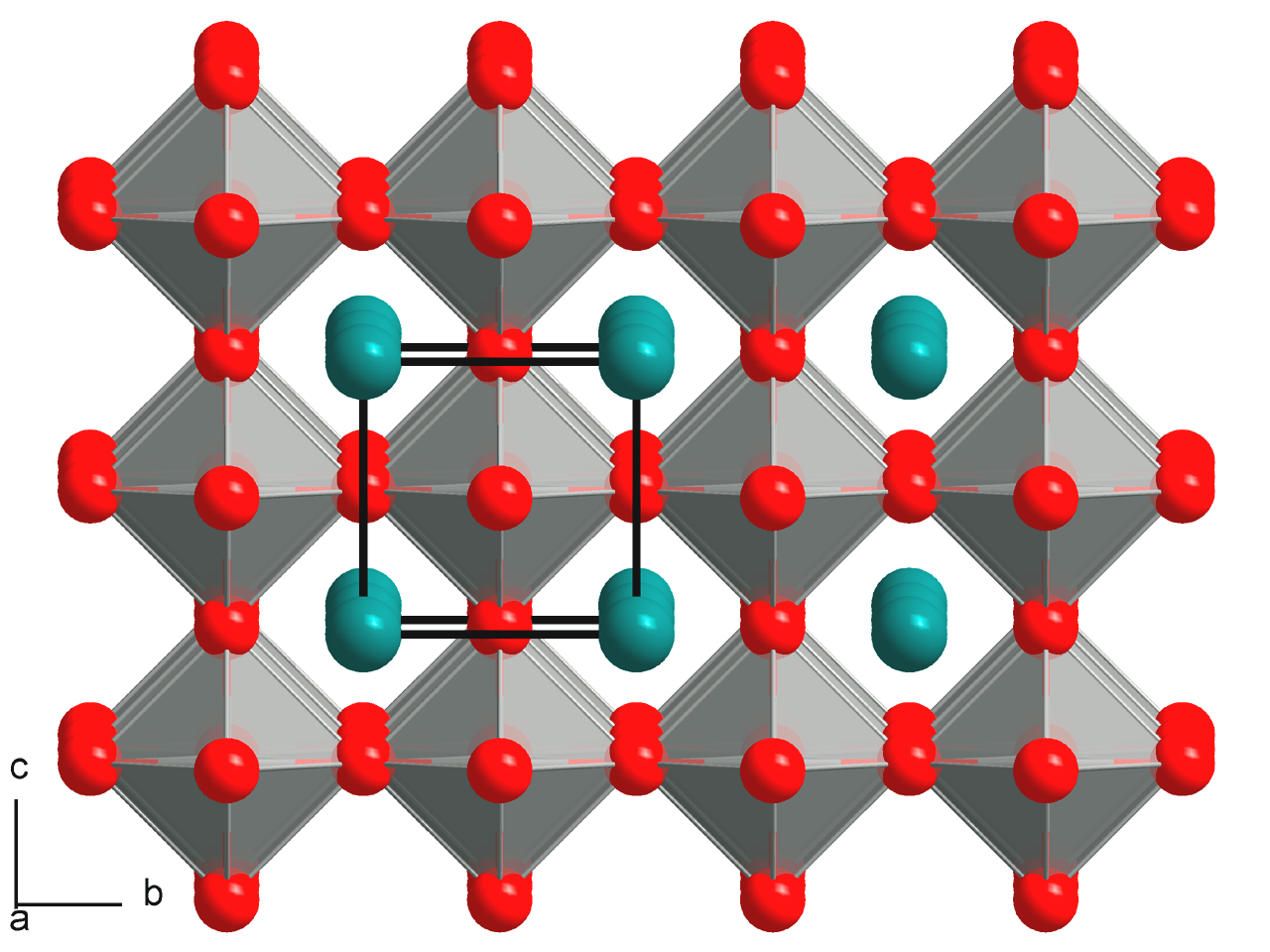
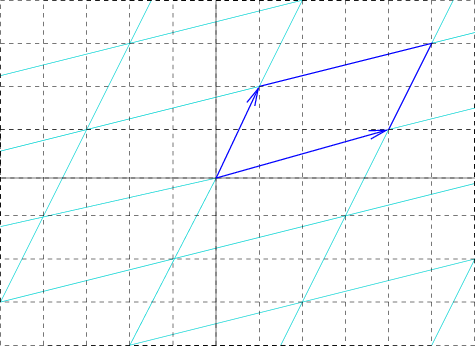
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumfle ..., for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |