|
Inverse Gamma Function
In mathematics, the inverse gamma function \Gamma^(x) is the inverse function of the gamma function. In other words, y = \Gamma^(x) whenever \Gamma(y)=x. For example, \Gamma^(24)=5. Usually, the inverse gamma function refers to the principal branch with domain on the real interval \left[\beta, +\infty\right) and image on the real interval \left[\alpha, +\infty\right), where \beta = 0.8856031\ldots is the minimum value of the gamma function on the positive real axis and \alpha = \Gamma^(\beta) = 1.4616321\ldots is the location of that minimum. Definition The inverse gamma function may be defined by the following integral representation \Gamma^(x)=a+bx+\int_^\left(\frac-\frac\right)d\mu(t)\,, where \mu (t) is a Borel measure such that \int_^\left(\frac\right)d\mu(t)<\infty \,, and and are real numbers with . Approximation To compute the branches of the inverse gamma function one can first compute th ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Borel Measure
In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets (and thus on all Borel sets). Some authors require additional restrictions on the measure, as described below. Formal definition Let X be a locally compact Hausdorff space, and let \mathfrak(X) be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. A Borel measure is any measure \mu defined on the σ-algebra of Borel sets. A few authors require in addition that \mu is locally finite, meaning that every point has an open neighborhood with finite measure. For Hausdorff spaces, this implies that \mu(C) 0 and ''μ''(''B''(''x'', ''r'')) ≤ ''rs'' holds for some constant ''s'' > 0 and for every ball ''B''(''x'', ''r'') in ''X'', then the Hausdorff dimension dimHaus(''X'') ≥ ''s''. A partial converse is provided by the Frostman lemma: Lemma: Let ''A'' be a Borel subset of R''n'', and let ''s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
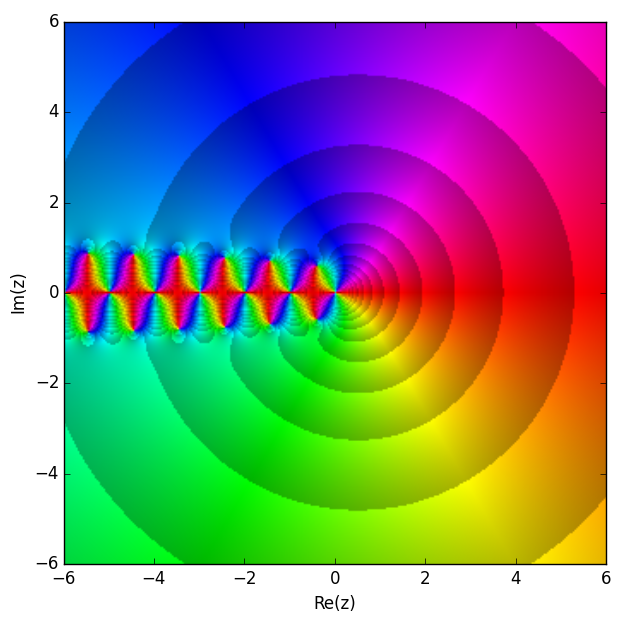 |
Trigamma Function
In mathematics, the trigamma function, denoted or , is the second of the polygamma functions, and is defined by : \psi_1(z) = \frac \ln\Gamma(z). It follows from this definition that : \psi_1(z) = \frac \psi(z) where is the digamma function. It may also be defined as the sum of the series : \psi_1(z) = \sum_^\frac, making it a special case of the Hurwitz zeta function : \psi_1(z) = \zeta(2,z). Note that the last two formulas are valid when is not a natural number. Calculation A double integral representation, as an alternative to the ones given above, may be derived from the series representation: : \psi_1(z) = \int_0^1\!\!\int_0^x\frac\,dy\,dx using the formula for the sum of a geometric series. Integration over yields: : \psi_1(z) = -\int_0^1\frac\,dx An asymptotic expansion as a Laurent series can be obtained via the derivative of the asymptotic expansion of the digamma function: :\begin \psi_1(z) &\sim \left(\ln z - \sum_^\infty \frac\right) \\ &= \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Asymptotic Formula
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior. As an illustration, suppose that we are interested in the properties of a function as becomes very large. If , then as becomes very large, the term becomes insignificant compared to . The function is said to be "''asymptotically equivalent'' to , as ". This is often written symbolically as , which is read as " is asymptotic to ". An example of an important asymptotic result is the prime number theorem. Let denote the prime-counting function (which is not directly related to the constant pi), i.e. is the number of prime numbers that are less than or equal to . Then the theorem states that \pi(x)\sim\frac. Asymptotic analysis is commonly used in computer science as part of the analysis of algorithms and is often expressed there in terms of big O notation. Definition Formally, given functions and , we define a binary relation f(x) \sim g(x) \quad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Lambert W Function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the Branch point, branches of the converse relation of the function , where is any complex number and is the exponential function. The function is named after Johann Heinrich Lambert, Johann Lambert, who considered a related problem in 1758. Building on Lambert's work, Leonhard Euler described the function per se in 1783. For each integer there is one branch, denoted by , which is a complex-valued function of one complex argument. is known as the principal branch. These functions have the following property: if and are any complex numbers, then : w e^ = z holds if and only if : w=W_k(z) \ \ \text k. When dealing with real numbers only, the two branches and suffice: for real numbers and the equation : y e^ = x can be solved for only if ; yields if and the two values and if . The Lambert function's branches cannot be expressed in terms o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Stirling's Approximation
In mathematics, Stirling's approximation (or Stirling's formula) is an asymptotic approximation for factorials. It is a good approximation, leading to accurate results even for small values of n. It is named after James Stirling, though a related but less precise result was first stated by Abraham de Moivre. One way of stating the approximation involves the logarithm of the factorial: \ln(n!) = n\ln n - n +O(\ln n), where the big O notation means that, for all sufficiently large values of n, the difference between \ln(n!) and n\ln n-n will be at most proportional to the logarithm of n. In computer science applications such as the worst-case lower bound for comparison sorting, it is convenient to instead use the binary logarithm, giving the equivalent form \log_2 (n!) = n\log_2 n - n\log_2 e +O(\log_2 n). The error term in either base can be expressed more precisely as \tfrac12\log(2\pi n)+O(\tfrac1n), corresponding to an approximate formula for the factorial itself, n! \sim \sqr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Polygamma Function
In mathematics, the polygamma function of order is a meromorphic function on the complex numbers \mathbb defined as the th derivative of the logarithm of the gamma function: :\psi^(z) := \frac \psi(z) = \frac \ln\Gamma(z). Thus :\psi^(z) = \psi(z) = \frac holds where is the digamma function and is the gamma function. They are holomorphic on \mathbb \backslash\mathbb_. At all the nonpositive integers these polygamma functions have a pole of order . The function is sometimes called the trigamma function. Integral representation When and , the polygamma function equals :\begin \psi^(z) &= (-1)^\int_0^\infty \frac\,\mathrmt \\ &= -\int_0^1 \frac(\ln t)^m\,\mathrmt\\ &= (-1)^m!\zeta(m+1,z) \end where \zeta(s,q) is the Hurwitz zeta function. This expresses the polygamma function as the Laplace transform of . It follows from Bernstein's theorem on monotone functions that, for and real and non-negative, is a completely monotone function. Setting in the above ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |