 |
Introduction To The Analysis Of The Infinite
''Introductio in analysin infinitorum'' (Latin: ''Introduction to the Analysis of the Infinite'') is a two-volume work by Leonhard Euler which lays the foundations of mathematical analysis. Written in Latin and published in 1748, the ''Introductio'' contains 18 chapters in the first part and 22 chapters in the second. It has Eneström numbers E101 and E102. It is considered the first precalculus book. Contents Chapter 1 is on the concepts of variables and functions. Chapters 2 and 3 are concerned with the transformation of functions. Chapter 4 introduces infinite series through rational functions. According to Henk Bos, :The ''Introduction'' is meant as a survey of concepts and methods in analysis and analytic geometry preliminary to the study of the differential and integral calculus. ulermade of this survey a masterly exercise in introducing as much as possible of analysis without using differentiation or integration. In particular, he introduced the elementary transcend ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Hyperbola E
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component (topology), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Besides being a conic section, a hyperbola can arise as the locus (mathematics), locus of points whose difference of distances to two fixed focus (geometry), foci is constant, as a curve for each point of which the rays to two fix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Transcendental Function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation whose coefficients are functions of the independent variable that can be written using only the basic operations of addition, subtraction, multiplication, and division (without the need of taking limits). This is in contrast to an algebraic function. Examples of transcendental functions include the exponential function, the logarithm function, the hyperbolic functions, and the trigonometric functions. Equations over these expressions are called transcendental equations. Definition Formally, an analytic function f of one real or complex variable is transcendental if it is algebraically independent of that variable. This means the function does not satisfy any polynomial equation. For example, the function f given by :f(x)=\frac for all x is not transcendental, but algebraic, because it satisfies the polynomial equation :(ax+b)-(cx+d)f(x)=0. Similarly, the functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. The editor-in-chief An editor-in-chief (EIC), also known as lead editor or chief editor, is a publication's editorial leader who has final responsibility for its operations and policies. The editor-in-chief heads all departments of the organization and is held accoun ... is Vadim Ponomarenko ( San Diego State University). The journal gives the Lester R. Ford Award annually to "authors of articles of expository excellence" published in the journal. Editors-in-chief The following persons are or have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Euclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid. ''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the works of earlier mathematicians such as Hippocrates of Chios, Eudoxus of Cnidus and Theaetetus (mathematician), Theaetetus, the ''Elements'' is a collection in 13 books of definitions, postulates, propositions and mathematical proofs that covers plane and solid Euclidean geometry, elementary number theory, and Commensurability (mathematics), incommensurable lines. These include Pythagorean theorem, Thales' theorem, the Euclidean algorithm for greatest common divisors, Euclid's theorem that there are infinitely many prime numbers, and the Compass-and-straightedge construction, construction of regular polygons and Regular polyhedra, polyhedra. Often referred to as the most successful textbook ever written, the ''Elements'' has continued to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Euclid
Euclid (; ; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of geometry that largely dominated the field until the early 19th century. His system, now referred to as Euclidean geometry, involved innovations in combination with a synthesis of theories from earlier Greek mathematicians, including Eudoxus of Cnidus, Hippocrates of Chios, Thales and Theaetetus. With Archimedes and Apollonius of Perga, Euclid is generally considered among the greatest mathematicians of antiquity, and one of the most influential in the history of mathematics. Very little is known of Euclid's life, and most information comes from the scholars Proclus and Pappus of Alexandria many centuries later. Medieval Islamic mathematicians invented a fanciful biography, and medieval Byzantine and early Renaissance scholars mistook him for the earlier philo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
International Congress Of Mathematicians
The International Congress of Mathematicians (ICM) is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union (IMU). The Fields Medals, the IMU Abacus Medal (known before 2022 as the Nevanlinna Prize), the Carl Friedrich Gauss Prize, Gauss Prize, and the Chern Medal are awarded during the congress's opening ceremony. Each congress is memorialized by a printed set of Proceedings recording academic papers based on invited talks intended to be relevant to current topics of general interest. Being List of International Congresses of Mathematicians Plenary and Invited Speakers, invited to talk at the ICM has been called "the equivalent ... of an induction to a hall of fame". History German mathematicians Felix Klein and Georg Cantor are credited with putting forward the idea of an international congress of mathematicians in the 1890s.A. John Coleman"Mathematics without borders": a book review. ''CMS Notes'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Carl Benjamin Boyer
Carl Benjamin Boyer (November 3, 1906 – April 26, 1976) was an American historian of sciences, and especially mathematics. Novelist David Foster Wallace called him the "Gibbon of math history". It has been written that he was one of few historians of mathematics of his time to "keep open links with contemporary history of science." Life and career Boyer was valedictorian of his high school class. He received a B.A. from Columbia College in 1928 and an M.A. in 1929. He received his Ph.D. in Mathematics from Columbia University in 1939. He was a full professor of Mathematics at the City University of New York's Brooklyn College from 1952 until his death, although he had begun tutoring and teaching at Brooklyn College in 1928. Along with Carolyn Eisele of CUNY's Hunter College; C. Doris Hellman of the Pratt Institute, and later CUNY's Queens College; and Lynn Thorndike of Columbia University, Boyer was instrumental in the 1953 founding of the Metropolitan New York Sectio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Continued Fraction
A continued fraction is a mathematical expression that can be written as a fraction with a denominator that is a sum that contains another simple or continued fraction. Depending on whether this iteration terminates with a simple fraction or not, the continued fraction is finite or infinite. Different fields of mathematics have different terminology and notation for continued fraction. In number theory the standard unqualified use of the term continued fraction refers to the special case where all numerators are 1, and is treated in the article simple continued fraction. The present article treats the case where numerators and denominators are sequences \,\ of constants or functions. From the perspective of number theory, these are called generalized continued fraction. From the perspective of complex analysis or numerical analysis, however, they are just standard, and in the present article they will simply be called "continued fraction". Formulation A continued fraction is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Number Theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example, rational numbers), or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory can often be understood through the study of Complex analysis, analytical objects, such as the Riemann zeta function, that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, as for instance how irrational numbers can be approximated by fractions (Diophantine approximation). Number theory is one of the oldest branches of mathematics alongside geometry. One quirk of number theory is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Partition (number Theory)
In number theory and combinatorics, a partition of a non-negative integer , also called an integer partition, is a way of writing as a sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition.) For example, can be partitioned in five distinct ways: : : : : : The only partition of zero is the empty sum, having no parts. The order-dependent composition is the same partition as , and the two distinct compositions and represent the same partition as . An individual summand in a partition is called a part. The number of partitions of is given by the partition function . So . The notation means that is a partition of . Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symmetric polynomials and of the symmetric group and in group representa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
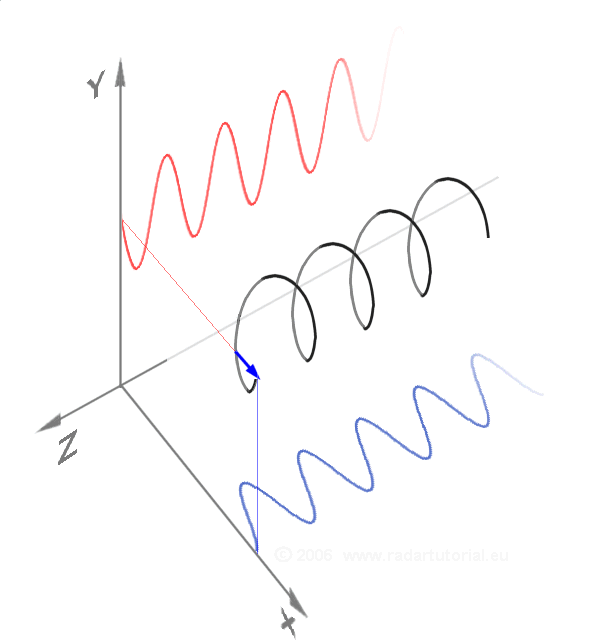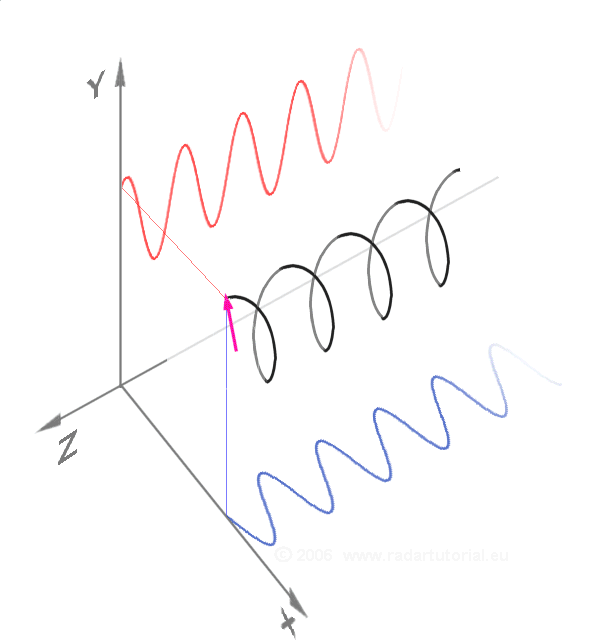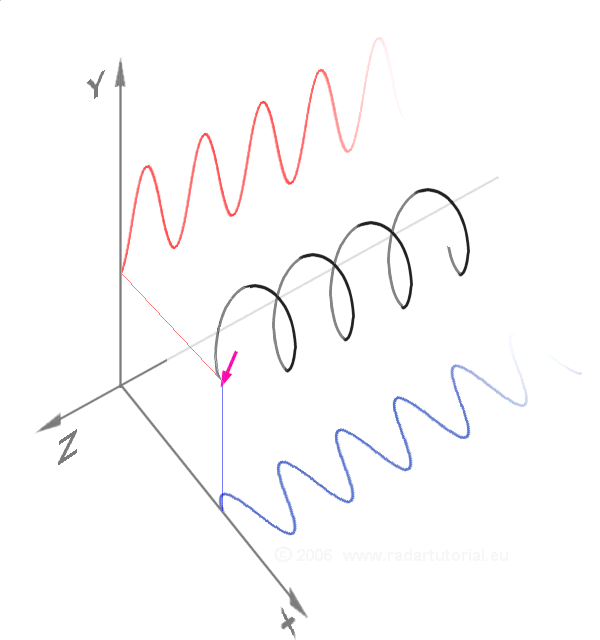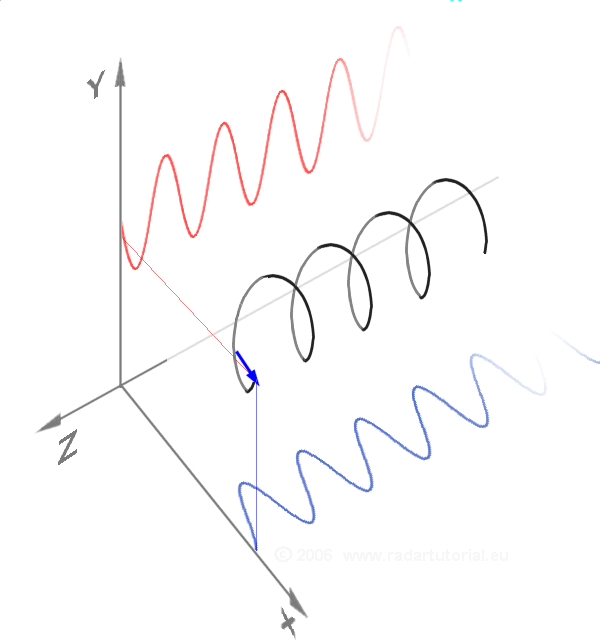 |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |