|
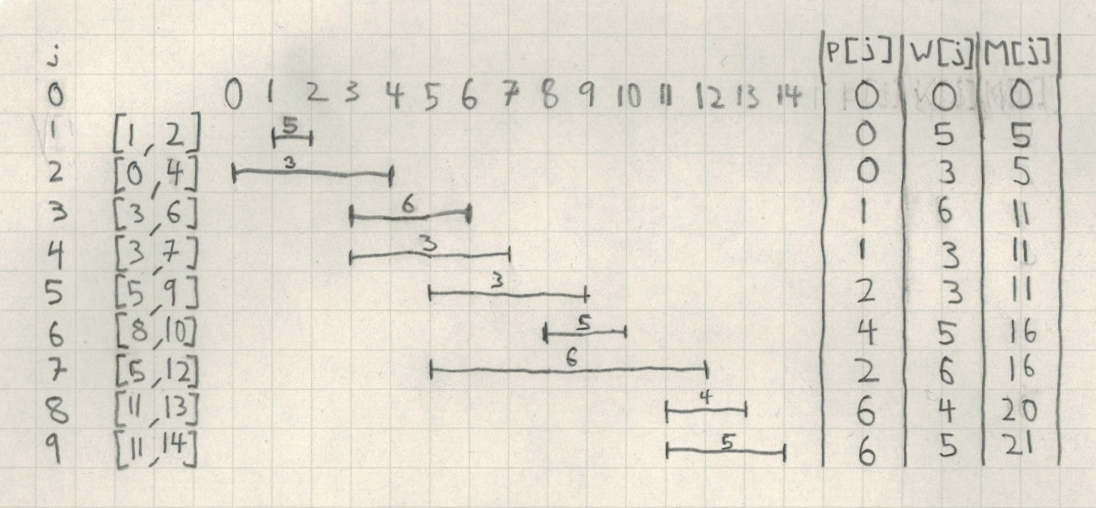
Interval Scheduling
Interval scheduling is a class of problems in computer science, particularly in the area of algorithm design. The problems consider a set of tasks. Each task is represented by an ''interval'' describing the time in which it needs to be processed by some machine (or, equivalently, scheduled on some resource). For instance, task A might run from 2:00 to 5:00, task B might run from 4:00 to 10:00 and task C might run from 9:00 to 11:00. A subset of intervals is ''compatible'' if no two intervals overlap on the machine/resource. For example, the subset is compatible, as is the subset ; but neither nor are compatible subsets, because the corresponding intervals within each subset overlap. The ''interval scheduling maximization problem'' (ISMP) is to find a largest compatible set, i.e., a set of non-overlapping intervals of maximum size. The goal here is to execute as many tasks as possible, that is, to maximize the throughput. It is equivalent to finding a Independent set (graph theor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''. Somewhat more precisely, a problem is NP-complete when: # It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no". # When the answer is "yes", this can be demonstrated through the existence of a short (polynomial length) ''solution''. # The correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. Hence, if we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-machine Scheduling
Single-machine scheduling or single-resource scheduling is an optimization problem in computer science and operations research. We are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on a single machine, in a way that optimizes a certain objective, such as the throughput. Single-machine scheduling is a special case of identical-machines scheduling, which is itself a special case of optimal job scheduling. Many problems, which are NP-hard in general, can be solved in polynomial time in the single-machine case. In the standard three-field notation for optimal job scheduling problems, the single-machine variant is denoted by 1 in the first field. For example, " 1, , \sum C_j" is a single-machine scheduling problem with no constraints, where the goal is to minimize the sum of completion times. The makespan-minimization problem 1, , C_, which is a common objective with multiple machines, is trivial with a single machine, since the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identical-machines Scheduling
Identical-machines scheduling is an optimization problem in computer science and operations research. We are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on ''m'' identical machines, such that a certain objective function is optimized, for example, the makespan is minimized. Identical machine scheduling is a special case of uniform machine scheduling, which is itself a special case of optimal job scheduling. In the general case, the processing time of each job may be different on different machines; in the case of identical machine scheduling, the processing time of each job is the same on each machine. Therefore, identical machine scheduling is equivalent to multiway number partitioning. A special case of identical machine scheduling is single-machine scheduling. In the standard three-field notation for optimal job scheduling problems, the identical-machines variant is denoted by P in the first field. For example, " P, , C_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Disjoint Set
In computational geometry, a maximum disjoint set (MDS) is a largest set of non-overlapping geometric shapes selected from a given set of candidate shapes. Every set of non-overlapping shapes is an independent set (graph theory), independent set in the intersection graph of the shapes. Therefore, the MDS problem is a special case of the maximum independent set (MIS) problem. Both problems are NP complete, but finding a MDS may be easier than finding a MIS in two respects: * For the general MIS problem, the best known exact algorithms are exponential. In some geometric intersection graphs, there are sub-exponential algorithms for finding a MDS. * The general MIS problem is hard to approximate and doesn't even have a constant-factor approximation. In some geometric intersection graphs, there are polynomial-time approximation schemes (PTAS) for finding a MDS. Finding an MDS is important in applications such as automatic label placement, VLSI circuit design, and cellular frequency divi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earliest Deadline First Scheduling
Earliest deadline first (EDF) or least time to go is a dynamic priority scheduling algorithm used in real-time operating systems to place processes in a priority queue. Whenever a scheduling event occurs (task finishes, new task released, etc.) the queue will be searched for the process closest to its deadline. This process is the next to be scheduled for execution. EDF is an ''optimal'' scheduling algorithm on preemptive uniprocessors, in the following sense: if a collection of independent ''jobs,'' each characterized by an arrival time, an execution requirement and a deadline, can be scheduled (by any algorithm) in a way that ensures all the jobs complete by their deadline, the EDF will schedule this collection of jobs so they all complete by their deadline. With scheduling periodic processes that have deadlines equal to their periods, EDF has a utilization bound of 100%. Thus, the schedulability test for EDF is: :U = \sum_^ \frac \leq 1, where the \left\ are the worst-case com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersection Graph
In graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph can be represented as an intersection graph, but some important special classes of graphs can be defined by the types of sets that are used to form an intersection representation of them. Formal definition Formally, an intersection graph is an undirected graph formed from a family of sets : S_i, \,\,\, i = 0, 1, 2, \dots by creating one vertex for each set , and connecting two vertices and by an edge whenever the corresponding two sets have a nonempty intersection, that is, : E(G) = \. All graphs are intersection graphs Any undirected graph may be represented as an intersection graph. For each vertex of , form a set consisting of the edges incident to ; then two such sets have a nonempty intersection if and only if the corresponding vertices share an edge. Therefore, is the intersection graph of the sets . provide a construction that is more ef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Operations Research
''Mathematics of Operations Research'' is a quarterly peer-reviewed scientific journal established in February 1976. It focuses on areas of mathematics relevant to the field of operations research such as continuous optimization, discrete optimization, game theory, machine learning, simulation methodology, and stochastic models. The journal is published by INFORMS (Institute for Operations Research and the Management Sciences). the journal has a 2017 impact factor of 1.078. History The journal was established in 1976. The founding editor-in-chief was Arthur F. Veinott Jr. (Stanford University). He served until 1980, when the position was taken over by Stephen M. Robinson, who held the position until 1986. Erhan Cinlar served from 1987 to 1992, and was followed by Jan Karel Lenstra (1993-1998). Next was Gérard Cornuéjols (1999-2003) and Nimrod Megiddo (2004-2009). Finally came Uri Rothblum (2009-2012), Jim Dai (2012-2018), and the current editor-in-chief Katya Scheinberg (20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming Relaxation
In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable. For example, in a 0–1 integer program, all constraints are of the form :x_i\in\. The relaxation of the original integer program instead uses a collection of linear constraints :0 \le x_i \le 1. The resulting relaxation is a linear program, hence the name. This relaxation technique transforms an NP-hard optimization problem (integer programming) into a related problem that is solvable in polynomial time (linear programming); the solution to the relaxed linear program can be used to gain information about the solution to the original integer program. Example Consider the set cover problem, the linear programming relaxation of which was first considered by Lovász in 1975. In this problem, one is given as input a family of sets ''F'' = ; the task is to find a subfamily, with as few sets as possible, having the same union as ''F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MaxSNP
In computational complexity theory, SNP (from Strict NP) is a complexity class containing a limited subset of NP based on its logical characterization in terms of graph-theoretical properties. It forms the basis for the definition of the class MaxSNP of optimization problems. It is defined as the class of problems that are properties of relational structures (such as graphs) expressible by a second-order logic formula of the following form: : \exists S_1 \dots \exists S_\ell \, \forall v_1 \dots \forall v_m \,\phi(R_1,\dots,R_k,S_1,\dots,S_\ell,v_1,\dots,v_m) where R_1,\dots,R_k are relations of the structure (such as the adjacency relation, for a graph), S_1,\dots,S_\ell are unknown relations (sets of tuples of vertices), and \phi is a quantifier-free formula: any boolean combination of the relations. That is, only existential second-order quantification (over relations) is allowed and only universal first-order quantification (over vertices) is allowed. If existential quantifi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2-SAT
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time. Instances of the 2-satisfiability problem are typically expressed as Boolean formulas of a special type, called conjunctive normal form (2-CNF) or Krom formulas. Alternatively, they may be expressed as a special type of directed graph, the implication graph, which expresses the variables of an instance and their negations as vertices in a graph, and constraints on pairs of variables as directed edges. Both o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2-satisfiability
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time. Instances of the 2-satisfiability problem are typically expressed as Boolean formulas of a special type, called conjunctive normal form (2-CNF) or Krom formulas. Alternatively, they may be expressed as a special type of directed graph, the implication graph, which expresses the variables of an instance and their negations as vertices in a graph, and constraints on pairs of variables as directed edges. Both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |