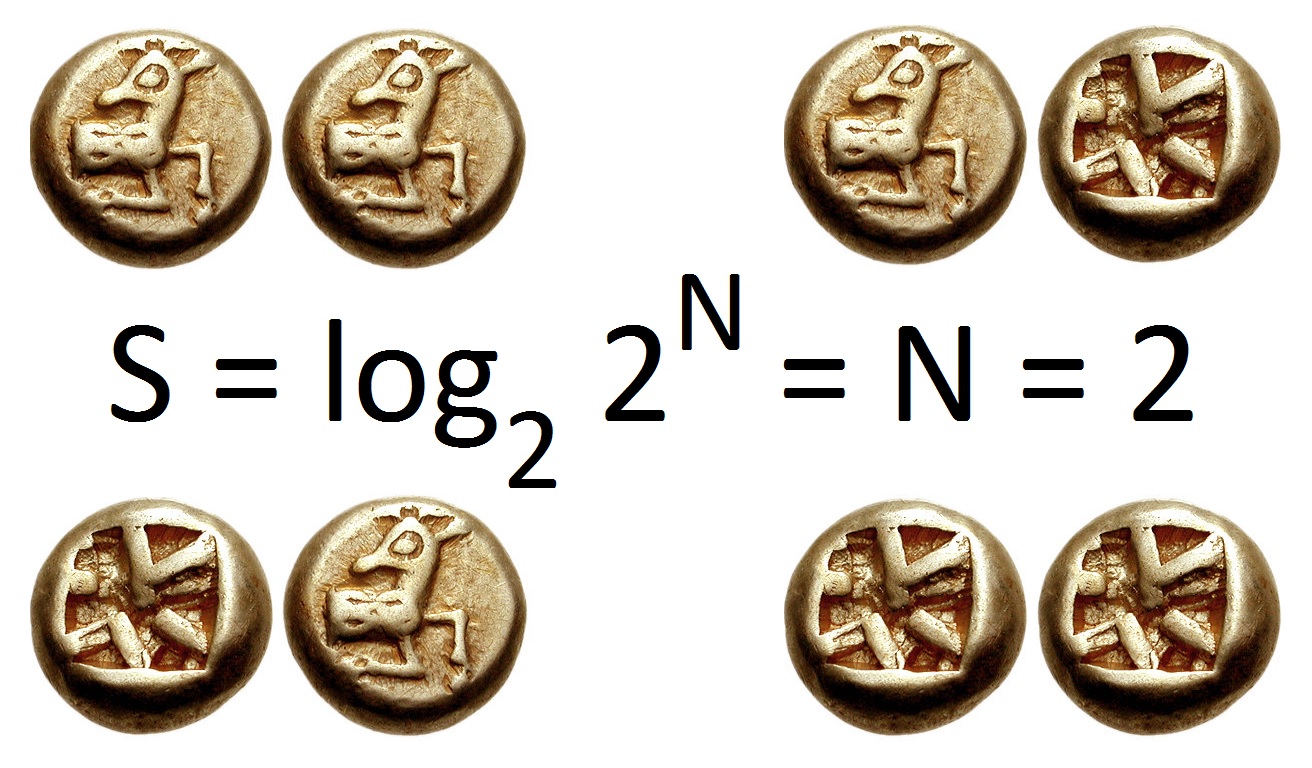|
Information Diagram
An information diagram is a type of Venn diagram used in information theory to illustrate relationships among Shannon's basic measures of information: entropy, joint entropy, conditional entropy and mutual information. Information diagrams are a useful pedagogical tool for teaching and learning about these basic measures of information. Information diagrams have also been applied to specific problems such as for displaying the information theoretic similarity between sets of ontological terms. Entropy-mutual-information-relative-entropy-relation-diagram.svg, Venn diagram showing additive and subtractive relationships among various information measures associated with correlated variables and . The area contained by both circles is the joint entropy . The circle on the left (red and violet) is the individual entropy , with the red being the conditional entropy H(X, Y). The circle on the right (blue and violet) is , with the blue being H(Y, X). The violet is the mutual inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Venn Diagram
A Venn diagram is a widely used diagram style that shows the logical relation between sets, popularized by John Venn (1834–1923) in the 1880s. The diagrams are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses simple closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses. Similar ideas had been proposed before Venn. Christian Weise in 1712 (''Nucleus Logicoe Wiesianoe'') and Leonhard Euler ('' Letters to a German Princess'') in 1768, for instance, came up with similar ideas. The idea was popularised by Venn in ''Symbolic Logic'', Chapter V "Diagrammatic Representation", 1881. Details A Venn diagram may also be called a ''set diagram'' or ''logic diagram''. It is a diagram that shows ''all'' possible logical relations between a finite collection of different sets. These diagrams depict elements as points in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Theory
Information theory is the scientific study of the quantification, storage, and communication of information. The field was originally established by the works of Harry Nyquist and Ralph Hartley, in the 1920s, and Claude Shannon in the 1940s. The field is at the intersection of probability theory, statistics, computer science, statistical mechanics, information engineering, and electrical engineering. A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a die (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy. Important sub-fields of information theory include s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantities Of Information
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of "more", "less", or "equal", or by assigning a numerical value multiple of a unit of measurement. Mass, time, distance, heat, and angle are among the familiar examples of quantitative properties. Quantity is among the basic classes of things along with quality, substance, change, and relation. Some quantities are such by their inner nature (as number), while others function as states (properties, dimensions, attributes) of things such as heavy and light, long and short, broad and narrow, small and great, or much and little. Under the name of multitude comes what is discontinuous and discrete and divisible ultimately into indivisibles, such as: ''army, fleet, flock, government, company, party, people, mess (military), chorus, crowd'', and ''number''; all which are cases of collective nouns. Under the name of magnitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Entropy
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to, 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper " A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joint Entropy
In information theory, joint entropy is a measure of the uncertainty associated with a set of variables. Definition The joint Shannon entropy (in bits) of two discrete random variables X and Y with images \mathcal X and \mathcal Y is defined as where x and y are particular values of X and Y, respectively, P(x,y) is the joint probability of these values occurring together, and P(x,y) \log_2 (x,y)/math> is defined to be 0 if P(x,y)=0. For more than two random variables X_1, ..., X_n this expands to where x_1,...,x_n are particular values of X_1,...,X_n, respectively, P(x_1, ..., x_n) is the probability of these values occurring together, and P(x_1, ..., x_n) \log_2 (x_1, ..., x_n)/math> is defined to be 0 if P(x_1, ..., x_n)=0. Properties Nonnegativity The joint entropy of a set of random variables is a nonnegative number. :\Eta(X,Y) \geq 0 :\Eta(X_1,\ldots, X_n) \geq 0 Greater than individual entropies The joint entropy of a set of variables is greater than or equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Entropy
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable Y given that the value of another random variable X is known. Here, information is measured in shannons, nats, or hartleys. The ''entropy of Y conditioned on X'' is written as \Eta(Y, X). Definition The conditional entropy of Y given X is defined as where \mathcal X and \mathcal Y denote the support sets of X and Y. ''Note:'' Here, the convention is that the expression 0 \log 0 should be treated as being equal to zero. This is because \lim_ \theta\, \log \theta = 0. Intuitively, notice that by definition of expected value and of conditional probability, \displaystyle H(Y, X) can be written as H(Y, X) = \mathbb (X,Y)/math>, where f is defined as \displaystyle f(x,y) := -\log\Big(\frac\Big) = -\log(p(y, x)). One can think of \displaystyle f as associating each pair \displaystyle (x, y) with a quantity measuring the information conten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Information
In probability theory and information theory, the mutual information (MI) of two random variables is a measure of the mutual dependence between the two variables. More specifically, it quantifies the " amount of information" (in units such as shannons (bits), nats or hartleys) obtained about one random variable by observing the other random variable. The concept of mutual information is intimately linked to that of entropy of a random variable, a fundamental notion in information theory that quantifies the expected "amount of information" held in a random variable. Not limited to real-valued random variables and linear dependence like the correlation coefficient, MI is more general and determines how different the joint distribution of the pair (X,Y) is from the product of the marginal distributions of X and Y. MI is the expected value of the pointwise mutual information (PMI). The quantity was defined and analyzed by Claude Shannon in his landmark paper " A Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Distance
Information distance is the distance between two finite objects (represented as computer files) expressed as the number of bits in the shortest program which transforms one object into the other one or vice versa on a universal computer. This is an extension of Kolmogorov complexity. The Kolmogorov complexity of a ''single'' finite object is the information in that object; the information distance between a ''pair'' of finite objects is the minimum information required to go from one object to the other or vice versa. Information distance was first defined and investigated in based on thermodynamic principles, see also. Subsequently, it achieved final form in. It is applied in the normalized compression distance and the normalized Google distance. Properties Formally the information distance ID(x,y) between x and y is defined by : ID(x,y) = \min \, with p a finite binary program for the fixed universal computer with as inputs finite binary strings x,y. In it is proven that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ontology (information Science)
In computer science and information science, an ontology encompasses a representation, formal naming, and definition of the categories, properties, and relations between the concepts, data, and entities that substantiate one, many, or all domains of discourse. More simply, an ontology is a way of showing the properties of a subject area and how they are related, by defining a set of concepts and categories that represent the subject. Every academic discipline or field creates ontologies to limit complexity and organize data into information and knowledge. Each uses ontological assumptions to frame explicit theories, research and applications. New ontologies may improve problem solving within that domain. Translating research papers within every field is a problem made easier when experts from different countries maintain a controlled vocabulary of jargon between each of their languages. For instance, the definition and ontology of economics is a primary concern in Marxist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlated Variables
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the so-called demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. Howev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable is the average level of "information", "surprise", or "uncertainty" inherent to the variable's possible outcomes. Given a discrete random variable X, which takes values in the alphabet \mathcal and is distributed according to p: \mathcal\to , 1/math>: \Eta(X) := -\sum_ p(x) \log p(x) = \mathbb \log p(X), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was introduced by Claude Shannon in his 1948 paper "A Mathematical Theory of Communication",PDF archived froherePDF archived frohere and is also referred to as Shannon entropy. Shannon's theory def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Entropy
In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable Y given that the value of another random variable X is known. Here, information is measured in shannons, nats, or hartleys. The ''entropy of Y conditioned on X'' is written as \Eta(Y, X). Definition The conditional entropy of Y given X is defined as where \mathcal X and \mathcal Y denote the support sets of X and Y. ''Note:'' Here, the convention is that the expression 0 \log 0 should be treated as being equal to zero. This is because \lim_ \theta\, \log \theta = 0. Intuitively, notice that by definition of expected value and of conditional probability, \displaystyle H(Y, X) can be written as H(Y, X) = \mathbb (X,Y)/math>, where f is defined as \displaystyle f(x,y) := -\log\Big(\frac\Big) = -\log(p(y, x)). One can think of \displaystyle f as associating each pair \displaystyle (x, y) with a quantity measuring the information conten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |