|
Hexagonal Tiling
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a Truncation (geometry), truncated triangular tiling). English mathematician John Horton Conway, John Conway called it a hextille. The internal angle of the hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. It is one of List of regular polytopes#Euclidean tilings, three regular tilings of the plane. The other two are the triangular tiling and the square tiling. Structure and properties The hexagonal tiling has a structure consisting of a regular hexagon only as its prototile, sharing two vertices with other identical ones, an example of monohedral tiling. Each vertex at the tiling is surrounded by three regular hexagons, denoted as 6.6.6 by vertex configuration. The dual of a hexagonal tiling is triangular tiling, because the center of each hexagonal tiling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Regular Tiling
Euclidean Plane (mathematics), plane Tessellation, tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Johannes Kepler, Kepler in his (Latin language, Latin: ''The Harmony of the World'', 1619). Notation of Euclidean tilings Euclidean tilings are usually named after Cundy & Rollett’s notation. This notation represents (i) the number of vertices, (ii) the number of polygons around each vertex (arranged clockwise) and (iii) the number of sides to each of those polygons. For example: 36; 36; 34.6, tells us there are 3 vertices with 2 different vertex types, so this tiling would be classed as a ‘3-uniform (2-vertex types)’ tiling. Broken down, 36; 36 (both of different transitivity class), or (36)2, tells us that there are 2 vertices (denoted by the superscript 2), each with 6 equilateral 3-sided polygons (triangles). With a final vertex 34.6, 4 more contiguous equilateral triangles and a single re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Equilateral Triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties. The equilateral triangle can be found in various tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry. Properties An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its base. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Chicken Wire
The chicken (''Gallus gallus domesticus'') is a domesticated subspecies of the red junglefowl (''Gallus gallus''), originally native to Southeast Asia. It was first domesticated around 8,000 years ago and is now one of the most common and widespread domesticated animals in the world. Chickens are primarily kept for their meat and eggs, though they are also kept as pets. As of 2023, the global chicken population exceeds 26.5 billion, with more than 50 billion birds produced annually for consumption. Specialized breeds such as broilers and laying hens have been developed for meat and egg production, respectively. A hen bred for laying can produce over 300 eggs per year. Chickens are social animals with complex vocalizations and behaviors, and feature prominently in folklore, religion, and literature across many societies. Their economic importance makes them a central component of global animal husbandry and agriculture. Nomenclature Terms for chickens include: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Graphene
Graphene () is a carbon allotrope consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice, honeycomb planar nanostructure. The name "graphene" is derived from "graphite" and the suffix -ene, indicating the presence of double bonds within the carbon structure. Graphene is known for its exceptionally high Ultimate tensile strength, tensile strength, Electrical resistivity and conductivity, electrical conductivity, Transparency and translucency, transparency, and being the thinnest two-dimensional material in the world. Despite the nearly transparent nature of a single graphene sheet, graphite (formed from stacked layers of graphene) appears black because it absorbs all visible light wavelengths. On a microscopic scale, graphene is the strongest material ever measured. The existence of graphene was first theorized in 1947 by P. R. Wallace, Philip R. Wallace during his research on graphite's electronic properties, while the term ''graphen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
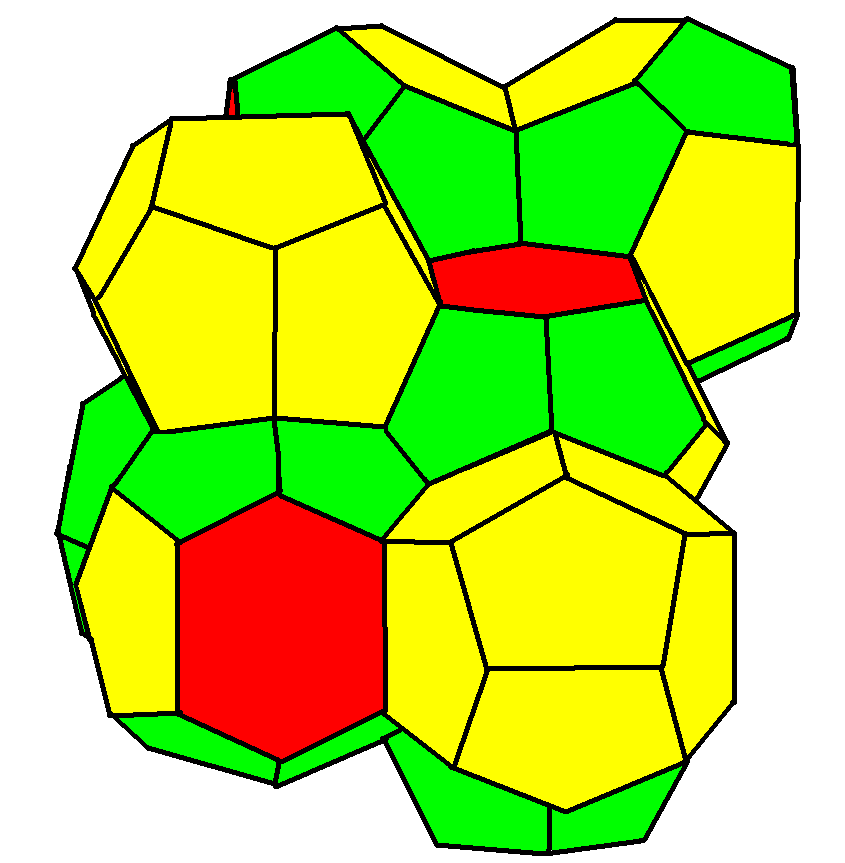 |
Weaire–Phelan Structure
In geometry, the Weaire–Phelan structure is a three-dimensional structure representing an idealised foam of equal-sized bubbles, with two different shapes. In 1993, Denis Weaire and Robert Phelan found that this structure was a better solution of the Kelvin problem of tiling space by equal volume cells of minimum surface area than the previous best-known solution, the Kelvin structure. History and the Kelvin problem In two dimensions, the subdivision of the plane into cells of equal area with minimum average perimeter is given by the hexagonal tiling, but although the first record of this honeycomb conjecture goes back to the ancient Roman scholar Marcus Terentius Varro (116-27 BCE), it was not proven until the work of Thomas C. Hales in 1999. In 1887, Lord Kelvin asked the corresponding question for three-dimensional space: how can space be partitioned into cells of equal volume with the least area of surface between them? Or, in short, what was the most efficient soap bubbl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Body-centered Cubic
In crystallography, the cubic (or isometric) crystal system is a crystal system where the Crystal structure#Unit cell, unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the Close-packing of equal spheres, ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive cell, primitiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Kelvin Structure
The kelvin (symbol: K) is the SI base unit, base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute scale, absolute temperature scale that starts at the lowest possible temperature (absolute zero), taken to be 0 K. By definition, the Celsius scale (symbol °C) and the Kelvin scale have the exact same magnitude; that is, a rise of 1 K is equal to a rise of 1 °C and vice versa, and any temperature in degrees Celsius can be converted to kelvin by adding 273.15. The 19th century British scientist Lord Kelvin first developed and proposed the scale. It was often called the "absolute Celsius" scale in the early 20th century. The kelvin was formally added to the International System of Units in 1954, defining 273.16 K to be the triple point of water. The Celsius, Fahrenheit, and Rankine scale, Rankine scales were redefined in terms of the Kelvin scale using this definition. The 2019 revision of the SI now defines the ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Lord Kelvin
William Thomson, 1st Baron Kelvin (26 June 182417 December 1907), was a British mathematician, Mathematical physics, mathematical physicist and engineer. Born in Belfast, he was the Professor of Natural Philosophy (Glasgow), professor of Natural Philosophy at the University of Glasgow for 53 years, where he undertook significant research on the mathematical analysis of electricity, was instrumental in the formulation of the first and second laws of thermodynamics, and contributed significantly to unifying physics, which was then in its infancy of development as an emerging academic discipline. He received the Royal Society's Copley Medal in 1883 and served as its President of the Royal Society, president from 1890 to 1895. In 1892, he became the first scientist to be elevated to the House of Lords. Absolute temperatures are stated in units of kelvin in Lord Kelvin's honour. While the existence of a coldest possible temperature, absolute zero, was known before his work, Kelvin d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Discrete And Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * ''Zentralblatt MATH'' * ''Science Citation Index'' * ''Current Contents'' Notable articles Two articles published in ''Discrete & Computational Geometry'', one by Gil Kalai in 1992 with a proof of a subexponential upper bound on the diameter of a polytope and another by Samuel Ferguson in 2006 on the Kepler conjecture on optimal three-dimensional sphere packing, earned their authors the Fulkerson Prize The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Honeycomb Theorem
The honeycomb theorem, formerly the honeycomb conjecture, states that a regular hexagonal grid or honeycomb has the least total perimeter of any subdivision of the plane into regions of equal area. The conjecture was proven in 1999 by mathematician Thomas C. Hales. Theorem Let \Gamma be any system of smooth curves in \mathbb^2, subdividing the plane into regions (connected components of the complement of \Gamma) all of which are bounded and have unit area. Then, averaged over large disks in the plane, the average length of \Gamma per unit area is at least as large as for the hexagon tiling. The theorem applies even if the complement of \Gamma has additional components that are unbounded or whose area is not one; allowing these additional components cannot shorten \Gamma. Formally, let B(0,r) denote the disk of radius r centered at the origin, let L_r denote the total length of \Gamma\cap B(0,r), and let A_r denote the total area of B(0,r) covered by bounded unit-area components ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Packing Density
A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest terms, this is the ratio of the volume of bodies in a space to the volume of the space itself. In packing problems, the objective is usually to obtain a packing of the greatest possible density. In compact spaces If are measurable subsets of a compact measure space and their interiors pairwise do not intersect, then the collection is a packing in and its packing density is :\eta=\frac. In Euclidean space If the space being packed is infinite in measure, such as Euclidean space, it is customary to define the density as the limit of densities exhibited in balls of larger and larger radii. If is the ball of radius centered at the origin, then the density of a packing is :\eta = \lim_\frac. Since this limit does not always exist, it is also useful to define the upper and lower densities as the limit superior and limit in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Sphere Packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions (where the problem becomes circle packing in two dimensions, or hypersphere packing in higher dimensions) or to Non-Euclidean geometry, non-Euclidean spaces such as hyperbolic space. A typical sphere packing problem is to find an arrangement in which the spheres fill as much of the space as possible. The proportion of space filled by the spheres is called the ''packing density'' of the arrangement. As the local density of a packing in an infinite space can vary depending on the volume over which it is measured, the problem is usually to maximise the average or asymptotic density, measured over a large enough volume. For equal spheres in three dimensions, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |