|
Hessian Matrix
In mathematics, the Hessian matrix, Hessian or (less commonly) Hesse matrix is a square matrix of second-order partial derivatives of a scalar-valued Function (mathematics), function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Otto Hesse, Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". The Hessian is sometimes denoted by H or \nabla\nabla or \nabla^2 or \nabla\otimes\nabla or D^2. Definitions and properties Suppose f : \R^n \to \R is a function taking as input a vector \mathbf \in \R^n and outputting a scalar f(\mathbf) \in \R. If all second-order partial derivatives of f exist, then the Hessian matrix \mathbf of f is a square n \times n matrix, usually defined and arranged as \mathbf H_f= \begin \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \dfrac & \dfrac & \cdots & \dfrac \\[2.2ex] \vdots & \vdot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematic
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Plane Curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomials : These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field . Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Of A Matrix
In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the part of the domain which is mapped to the zero vector of the co-domain; the kernel is always a linear subspace of the domain. That is, given a linear map between two vector spaces and , the kernel of is the vector space of all elements of such that , where denotes the zero vector in , or more symbolically: \ker(L) = \left\ = L^(\mathbf). Properties The kernel of is a linear subspace of the domain .Linear algebra, as discussed in this article, is a very well established mathematical discipline for which there are many sources. Almost all of the material in this article can be found in , , and Strang's lectures. In the linear map L : V \to W, two elements of have the same image in if and only if their difference lies in the kernel of , that is, L\left(\mathbf_1\right) = L\left(\mathbf_2\right) \quad \text \quad L\left(\mathbf_1-\mathbf_2\right) = \mathbf. From this, it follows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
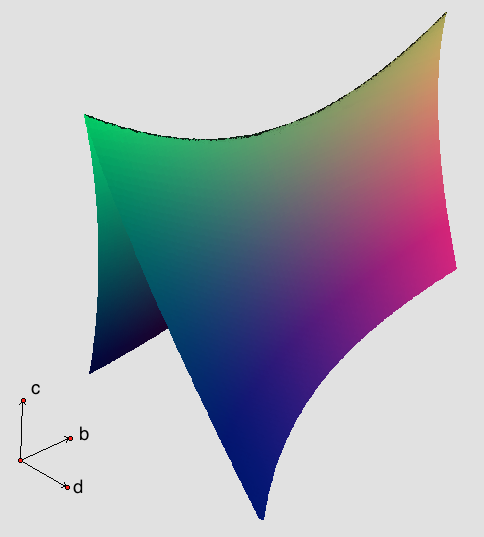
Catastrophe Theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry. Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analysing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, for example the unpredictable timing and magnitude of a landslide. Catastrophe theory originated with the work of the French mathematician René Thom in the 1960s, and became very popular due to the efforts of Christopher Zeeman in the 1970s. It considers the special case where the long-run stable equilibrium can be identified as the minimum of a smooth, well-defined potential function (Lyapunov function). Small changes in certain parameters of a nonlinear system can cause equilibria to appear or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the zero of a function, roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factorization, polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real number, real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stationary Point
In mathematics, particularly in calculus, a stationary point of a differentiable function of one variable is a point on the graph of a function, graph of the function where the function's derivative is zero. Informally, it is a point where the function "stops" increasing or decreasing (hence the name). For a differentiable function of several real variables, a stationary point is a point on the surface (mathematics), surface of the graph where all its partial derivatives are zero (equivalently, the gradient has zero vector norm, norm). The notion of stationary points of a real-valued function is generalized as ''Critical point (mathematics), critical points'' for complex-valued functions. Stationary points are easy to visualize on the graph of a function of one variable: they correspond to the points on the graph where the tangent is horizontal (i.e., Parallel (geometry), parallel to the Abscissa, -axis). For a function of two variables, they correspond to the points on the gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minor (linear Algebra)
In linear algebra, a minor of a matrix (mathematics), matrix is the determinant of some smaller square matrix generated from by removing one or more of its rows and columns. Minors obtained by removing just one row and one column from square matrices (first minors) are required for calculating matrix cofactors, which are useful for computing both the determinant and Inverse matrix, inverse of square matrices. The requirement that the square matrix be smaller than the original matrix is often omitted in the definition. Definition and illustration First minors If is a square matrix, then the ''minor'' of the entry in the -th row and -th column (also called the ''minor'', or a ''first minor'') is the determinant of the submatrix formed by deleting the -th row and -th column. This number is often denoted . The ''cofactor'' is obtained by multiplying the minor by . To illustrate these definitions, consider the following matrix, \begin 1 & 4 & 7 \\ 3 & 0 & 5 \\ -1 & 9 & 11 \\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morse Theory
In mathematics, specifically in differential topology, Morse theory enables one to analyze the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiable function on a manifold will reflect the topology quite directly. Morse theory allows one to find CW structures and handle decompositions on manifolds and to obtain substantial information about their homology. Before Morse, Arthur Cayley and James Clerk Maxwell had developed some of the ideas of Morse theory in the context of topography. Morse originally applied his theory to geodesics ( critical points of the energy functional on the space of paths). These techniques were used in Raoul Bott's proof of his periodicity theorem. The analogue of Morse theory for complex manifolds is Picard–Lefschetz theory. Basic concepts To illustrate, consider a mountainous landscape surface M (more generally, a manifold). If f is the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and a relative maxima and minima, maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface (mathematics), surface that ''curves up'' in one direction, and ''curves down'' in a different dir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |