|
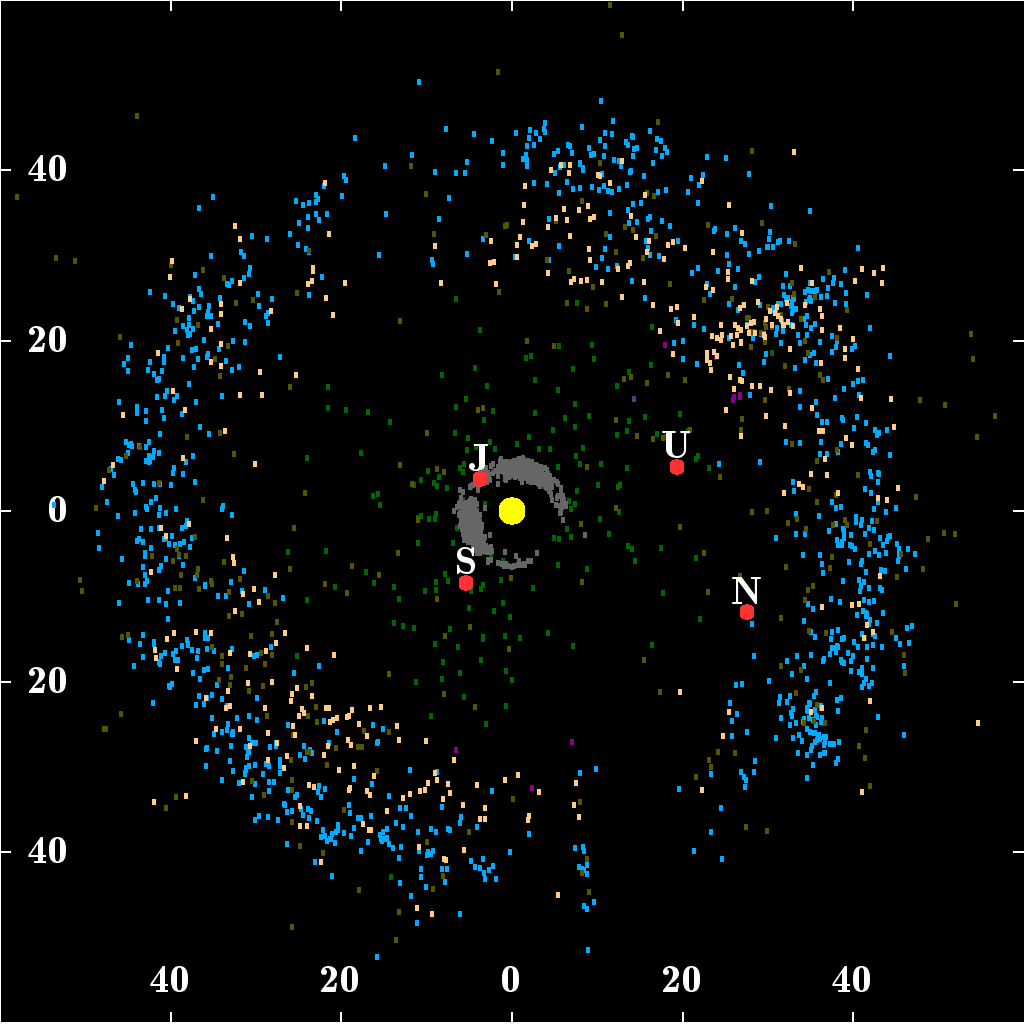
Haumea Family
The Haumea or Haumean family is the only identified Trans-Neptunian objects, trans-Neptunian collisional family; that is, the only group of trans-Neptunian objects (TNOs) with similar orbital parameters and spectra (nearly pure water-ice) that suggest they originated in the disruptive impact of a progenitor body. Calculations indicate that it is probably the only trans-Neptunian collisional family. Members are known as haumeids. Members Characteristics The dwarf planet is the largest member of the family, and the core of the differentiated progenitor; other identified members are the moons of Haumea and the Kuiper belt objects , , , , , , , , and , all with an ejection velocity from Haumea of less than 150 m/s. The brightest Haumeids have Absolute magnitude#Solar System bodies (H), absolute magnitudes (H) bright enough to suggest a size between 400 and 700 km in diameter, and so List of possible dwarf planets, possible dwarf planets, if they had the Albedo#Astrono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kuiper Belt Object
The Kuiper belt ( ) is a circumstellar disc in the outer Solar System, extending from the orbit of Neptune at 30 astronomical units (AU) to approximately 50 AU from the Sun. It is similar to the asteroid belt, but is far larger—20 times as wide and 20–200 times as massive. Like the asteroid belt, it consists mainly of small bodies or remnants from when the Solar System formed. While many asteroids are composed primarily of rock and metal, most Kuiper belt objects are composed largely of frozen volatiles (termed "ices"), such as methane, ammonia, and water. The Kuiper belt is home to most of the objects that astronomers generally accept as dwarf planets: Orcus, Pluto, Haumea, Quaoar, and Makemake. Some of the Solar System's moons, such as Neptune's Triton and Saturn's Phoebe, may have originated in the region. The Kuiper belt is named in honor of the Dutch astronomer Gerard Kuiper, who conjectured the existence of the belt in 1951. There were researchers befo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Anomaly
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit. Definition Define as the time required for a particular body to complete one orbit. In time , the radius vector sweeps out 2 radians, or 360°. The average rate of sweep, , is then n = \frac = \frac~, which is called the '' mean angular motion'' of the body, with dimensions of radians per unit time or degrees per unit time. Define as the time at which the body is at the pericenter. From the above definitions, a new quantity, , the ''mean anomaly'' can be defined M = n\,(t - \tau) ~, which gives an angul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
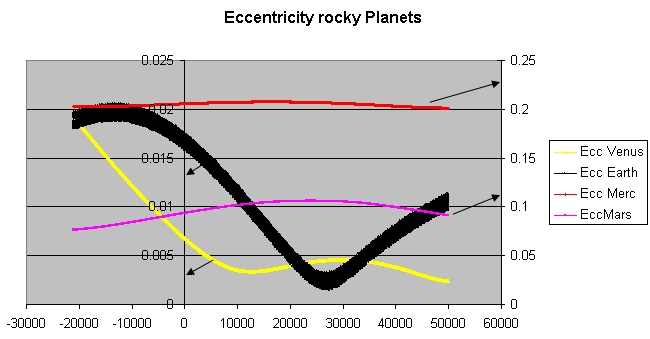
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degrees. For a satellite orbiting a planet, the plane of reference is usually the plane containing the planet's equator. For pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
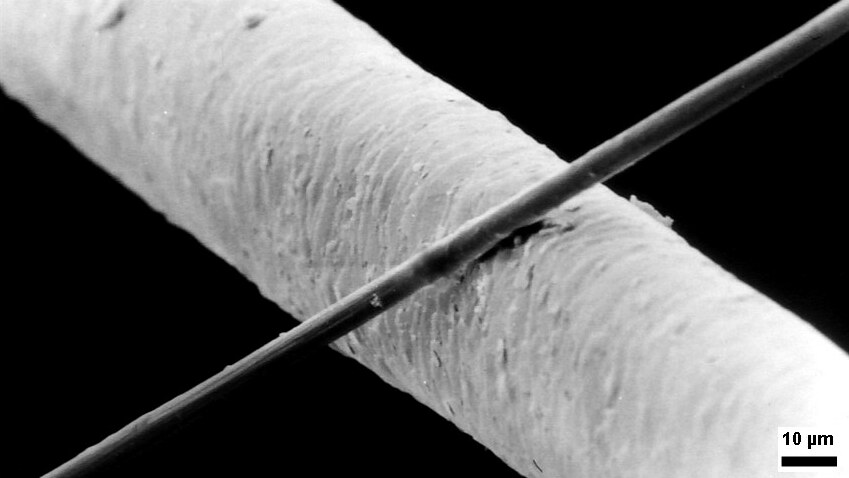
Micrometres
The micrometre (English in the Commonwealth of Nations, Commonwealth English as used by the International Bureau of Weights and Measures; SI symbol: μm) or micrometer (American English), also commonly known by the non-SI term micron, is a unit of length in the International System of Units (SI) equalling (SI standard prefix "micro-" = ); that is, one millionth of a metre (or one thousandth of a millimetre, , or about ). The nearest smaller common SI Unit, SI unit is the nanometre, equivalent to one thousandth of a micrometre, one millionth of a millimetre or one billionth of a metre (). The micrometre is a common unit of measurement for wavelengths of infrared radiation as well as sizes of biological cell (biology), cells and bacteria, and for grading wool by the diameter of the fibres. The width of a single human hair ranges from approximately 20 to . Examples Between 1 μm and 10 μm: * 1–10 μm – length of a typical bacterium * 3–8 μm – width of str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Color Index
In astronomy, the color index is a simple numerical expression that determines the color of an object, which in the case of a star gives its temperature. The lower the color index, the more blue (or hotter) the object is. Conversely, the larger the color index, the more red (or cooler) the object is. This is a consequence of the logarithmic magnitude scale, in which brighter objects have smaller (more negative) magnitudes than dimmer ones. For comparison, the whitish Sun has a B−V index of , whereas the bluish Rigel has a B−V of −0.03 (its B magnitude is 0.09 and its V magnitude is 0.12, B−V = −0.03). Traditionally, the color index uses Vega as a zero point. The blue supergiant Theta Muscae has one of the lowest B−V indices at −0.41, while the red giant and carbon star R Leporis has one of the largest, at +5.74. To measure the index, one observes the magnitude of an object successively through two different filters, such as U and B, or B and V, where U is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monthly Notices Of The Royal Astronomical Society
''Monthly Notices of the Royal Astronomical Society'' (MNRAS) is a peer-reviewed scientific journal in astronomy, astrophysics and related fields. It publishes original research in two formats: papers (of any length) and letters (limited to five pages). MNRAS publishes more articles per year than any other astronomy journal. The learned society journal has been in continuous existence since 1827 and became online only in 2020. It operates as a partnership between the Royal Astronomical Society (RAS), who select and peer-review the contents, and Oxford University Press (OUP), who publish and market the journal. Despite its name, MNRAS is no longer monthly, nor does it carry the notices of the RAS. In 2024 MNRAS became a purely gold open access journal. History The first issue of MNRAS was published on 9 February 1827 as ''Monthly Notices of the Astronomical Society of London'' and it has been in continuous publication ever since. It took its current name from the second vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbital Inclination
Orbital inclination measures the tilt of an object's orbit around a celestial body. It is expressed as the angle between a reference plane and the orbital plane or axis of direction of the orbiting object. For a satellite orbiting the Earth directly above the Equator, the plane of the satellite's orbit is the same as the Earth's equatorial plane, and the satellite's orbital inclination is 0°. The general case for a circular orbit is that it is tilted, spending half an orbit over the northern hemisphere and half over the southern. If the orbit swung between 20° north latitude and 20° south latitude, then its orbital inclination would be 20°. Orbits The inclination is one of the six orbital elements describing the shape and orientation of a celestial orbit. It is the angle between the orbital plane and the plane of reference, normally stated in degrees. For a satellite orbiting a planet, the plane of reference is usually the plane containing the planet's equator. For pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |