|
Halton Sequence
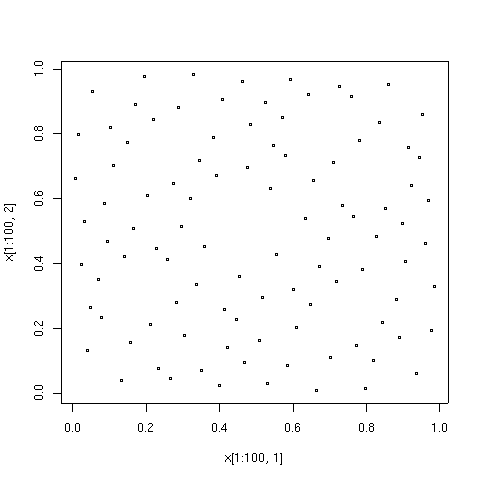
In statistics, Halton sequences are sequences used to generate points in space for numerical methods such as Monte Carlo simulations. Although these sequences are Deterministic system (mathematics), deterministic, they are of Low-discrepancy sequence, low discrepancy, that is, appear to be random for many purposes. They were first introduced in 1960 and are an example of a quasi-random number sequence. They generalize the one-dimensional van der Corput sequences. Example of Halton sequence used to generate points in (0, 1) × (0, 1) in R2 The Halton sequence is constructed according to a deterministic method that uses coprime integers, coprime numbers as its bases. As a simple example, let's take one dimension of the two-dimensional Halton sequence to be based on 2 and the other dimension on 3. To generate the sequence for 2, we start by dividing the interval (0,1) in half, then in fourths, eighths, etc., which generates : , : , , : , , , , : , ,... Equiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Pseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actions and conditions. Although pseudocode shares features with regular programming languages, it is intended for human reading rather than machine control. Pseudocode typically omits details that are essential for machine implementation of the algorithm, meaning that pseudocode can only be verified by hand. The programming language is augmented with natural language description details, where convenient, or with compact mathematical notation. The reasons for using pseudocode are that it is easier for people to understand than conventional programming language code and that it is an efficient and environment-independent description of the key principles of an algorithm. It is commonly used in textbooks and scientific publications to document ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Sequences And Series
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter "M" first and "Y" last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Low-discrepancy Sequences
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x_1, \ldots, x_N has a low discrepancy of a sequence, discrepancy. Roughly speaking, the discrepancy of a sequence is low if the proportion of points in the sequence falling into an arbitrary set ''B'' is close to proportional to the Measure (mathematics), measure of ''B'', as would happen on average (but not for particular samples) in the case of an equidistributed sequence. Specific definitions of discrepancy differ regarding the choice of ''B'' (hyperspheres, Hypercube, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value). Low-discrepancy sequences are also called quasirandom sequences, due to their common use as a replacement of uniformly distributed random sequence, random numbers. The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Society For Industrial And Applied Mathematics
Society for Industrial and Applied Mathematics (SIAM) is a professional society dedicated to applied mathematics, computational science, and data science through research, publications, and community. SIAM is the world's largest scientific society devoted to applied mathematics, and roughly two-thirds of its membership resides within the United States. Founded in 1951, the organization began holding annual national meetings in 1954, and now hosts conferences, publishes books and scholarly journals, and engages in advocacy in issues of interest to its membership. Members include engineers, scientists, and mathematicians, both those employed in academia and those working in industry. The society supports educational institutions promoting applied mathematics. SIAM is one of the four member organizations of the Joint Policy Board for Mathematics. Membership Membership is open to both individuals and organizations. By the end of its first full year of operation, SIAM had 130 me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Dover Publications
Dover Publications, also known as Dover Books, is an American book publisher founded in 1941 by Hayward and Blanche Cirker. It primarily reissues books that are out of print from their original publishers. These are often, but not always, books in the public domain. The original published editions may be scarce or historically significant. Dover republishes these books, making them available at a significantly reduced cost. Classic reprints Dover reprints classic works of literature, classical sheet music, and public-domain images from the 18th and 19th centuries. Dover also publishes an extensive collection of mathematical, scientific, and engineering texts. It often targets its reprints at a niche market, such as woodworking. Starting in 2015, the company branched out into graphic novel reprints, overseen by Dover acquisitions editor and former comics writer and editor Drew Ford. Most Dover reprints are photo facsimiles of the originals, retaining the original pagination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Constructions Of Low-discrepancy Sequences
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x_1, \ldots, x_N has a low discrepancy. Roughly speaking, the discrepancy of a sequence is low if the proportion of points in the sequence falling into an arbitrary set ''B'' is close to proportional to the measure of ''B'', as would happen on average (but not for particular samples) in the case of an equidistributed sequence. Specific definitions of discrepancy differ regarding the choice of ''B'' ( hyperspheres, hypercubes, etc.) and how the discrepancy for every B is computed (usually normalized) and combined (usually by taking the worst value). Low-discrepancy sequences are also called quasirandom sequences, due to their common use as a replacement of uniformly distributed random numbers. The "quasi" modifier is used to denote more clearly that the values of a low-discrepancy sequence are neither random nor pseudorandom, but such sequences share some propertie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Python (programming Language)
Python is a high-level programming language, high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is type system#DYNAMIC, dynamically type-checked and garbage collection (computer science), garbage-collected. It supports multiple programming paradigms, including structured programming, structured (particularly procedural programming, procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC (programming language), ABC programming language, and he first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000. Python 3.0, released in 2008, was a major revision not completely backward-compatible with earlier versions. Python 2.7.18, released in 2020, was the last release of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Generator (computer Programming)
In computer science, a generator is a routine that can be used to control the iteration behaviour of a loop. All generators are also iterators. A generator is very similar to a function that returns an array, in that a generator has parameters, can be called, and generates a sequence of values. However, instead of building an array containing all the values and returning them all at once, a generator ''yields'' the values one at a time, which requires less memory and allows the caller to get started processing the first few values immediately. In short, a generator ''looks like'' a function but ''behaves like'' an iterator. Generators can be implemented in terms of more expressive control flow constructs, such as coroutines or first-class continuations. Generators, also known as semicoroutines, are a special case of (and weaker than) coroutines, in that they always yield control back to the caller (when passing a value back), rather than specifying a coroutine to jump to; s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Linear Correlation
In statistics, correlation or dependence is any statistical relationship, whether causality, causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are ''line (geometry), linearly'' related. Familiar examples of dependent phenomena include the correlation between the human height, height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causality, causal relationship, because extreme weather causes people to use more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter "M" first and "Y" last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |