|
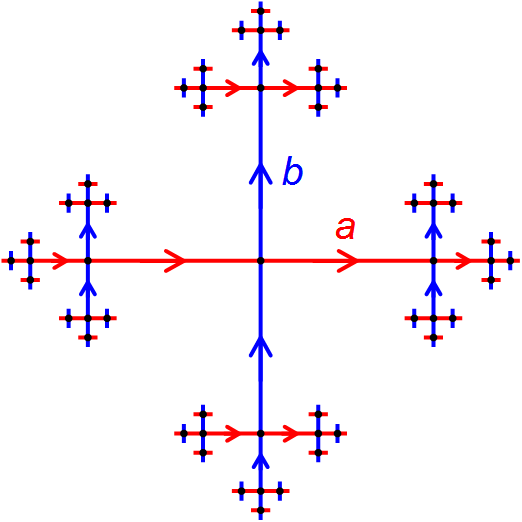
Graph Of Groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups. There is a unique group, called the fundamental group, canonically associated to each finite connected graph of groups. It admits an orientation-preserving action on a tree: the original graph of groups can be recovered from the quotient graph and the stabilizer subgroups. This theory, commonly referred to as Bass–Serre theory, is due to the work of Hyman Bass and Jean-Pierre Serre. Definition A graph of groups over a graph is an assignment to each vertex of of a group and to each edge of of a group as well as monomorphisms and mapping into the groups assigned to the vertices at its ends. Fundamental group Let be a spanning tree for and define the fundamental group to be the group generated by the vertex groups and elements for each edge of w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups can act non-trivially (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
HNN Extension
In mathematics, the HNN extension is an important construction of combinatorial group theory. Introduced in a 1949 paper ''Embedding Theorems for Groups'' by Graham Higman, Bernhard Neumann, and Hanna Neumann, it embeds a given group ''G'' into another group ''G' '', in such a way that two given isomorphic subgroups of ''G'' are conjugate (through a given isomorphism) in ''G' ''. Construction Let ''G'' be a group with presentation G = \langle S \mid R\rangle , and let \alpha\colon H \to K be an isomorphism between two subgroups of ''G''. Let ''t'' be a new symbol not in ''S'', and define :G*_ = \left \langle S,t \mid R, tht^=\alpha(h), \forall h\in H \right \rangle. The group G*_ is called the ''HNN extension of'' ''G'' ''relative to'' α. The original group G is called the ''base group'' for the construction, while the subgroups ''H'' and ''K'' are the ''associated subgroups''. The new generator ''t'' is called the ''stable letter''. Key properties Since the presentation fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mikhail Gromov (mathematician)
Mikhael Leonidovich Gromov (also Mikhail Gromov, Michael Gromov or Misha Gromov; ; born 23 December 1943) is a Russian-French mathematician known for his work in geometry, analysis and group theory. He is a permanent member of Institut des Hautes Études Scientifiques in France and a professor of mathematics at New York University. Gromov has won several prizes, including the Abel Prize in 2009 "for his revolutionary contributions to geometry". Early years, education and career Mikhail Gromov was born on 23 December 1943 in Boksitogorsk, Soviet Union. His father Leonid Gromov was Russian-Slavic and his mother Lea was of Jewish heritage. Both were pathologists. His mother was the cousin of World Chess Champion Mikhail Botvinnik, as well as of the mathematician Isaak Moiseevich Rabinovich. Gromov was born during World War II, and his mother, who worked as a medical doctor in the Soviet Army, had to leave the front line in order to give birth to him. When Gromov was nine years ol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Link (geometry)
The link in a simplicial complex is a generalization of the neighborhood of a vertex in a graph. The link of a vertex encodes information about the local structure of the complex at the vertex. Link of a vertex Given an abstract simplicial complex and v a vertex in V(X), its link \operatorname(v,X) is a set containing every face \tau \in X such that v\not\in \tau and \tau\cup \ is a face of . * In the special case in which is a 1-dimensional complex (that is: a graph), \operatorname(v,X) contains all vertices u\neq v such that \ is an edge in the graph; that is, \operatorname(v, X)=\mathcal(v)=the neighborhood system of v in the graph. Given a geometric simplicial complex and v\in V(X), its link \operatorname(v,X) is a set containing every face \tau \in X such that v\not\in \tau and there is a simplex in X that has v as a vertex and \tau as a face. Equivalently, the join v \star \tau is a face in X. * As an example, suppose v is the top vertex of the tetrahedron at t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glossary Of Graph Theory
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges. Symbols A B C D E F G H I J K L M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CAT(k) Space
In mathematics, a \mathbf(k) space, where k is a real number, is a specific type of metric space. Intuitively, triangles in a \operatorname(k) space (with k0. Let (X,d) be a geodesic metric space, i.e. a metric space for which every two points x,y\in X can be joined by a geodesic segment, an arc length parametrized continuous curve \gamma\colon ,b\to X,\ \gamma(a) = x,\ \gamma(b) = y, whose length :L(\gamma) = \sup \left\ is precisely d(x,y). Let \Delta be a triangle in X with geodesic segments as its sides. \Delta is said to satisfy the \mathbf(k) inequality if there is a comparison triangle \Delta' in the model space M_k, with sides of the same length as the sides of \Delta, such that distances between points on \Delta are less than or equal to the distances between corresponding points on \Delta'. The geodesic metric space (X,d) is said to be a \mathbf(k) space if every geodesic triangle \Delta in X with perimeter less than 2D_k satisfies the \operatorname(k) inequality. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplicial Complex
In mathematics, a simplicial complex is a structured Set (mathematics), set composed of Point (geometry), points, line segments, triangles, and their ''n''-dimensional counterparts, called Simplex, simplices, such that all the faces and intersections of the elements are also included in the set (see illustration). Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely Combinatorics, combinatorial counterpart to a simplicial complex is an abstract simplicial complex. To distinguish a simplicial complex from an abstract simplicial complex, the former is often called a geometric simplicial complex., Section 4.3 Definitions A simplicial complex \mathcal is a set of Simplex, simplices that satisfies the following conditions: # Every Simplex#Elements, face of a simplex from \mathcal is also in \mathcal. # The non-empty Set intersection, intersection of any two simplices \sigma_1, \sigma_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Properly Discontinuous
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter–Dynkin Diagram
In geometry, a Harold Scott MacDonald Coxeter, Coxeter–Eugene Dynkin, Dynkin diagram (or Coxeter diagram, Coxeter graph) is a Graph (discrete mathematics), graph with numerically labeled edges (called branches) representing a Coxeter group or sometimes a uniform polytope or uniform tiling constructed from the group. A class of closely related objects is the Dynkin diagrams, which differ from Coxeter diagrams in two respects: firstly, branches labeled "" or greater are Directed graph, directed, while Coxeter diagrams are Undirected graph, undirected; secondly, Dynkin diagrams must satisfy an additional (Crystallographic restriction theorem, crystallographic) restriction, namely that the only allowed branch labels are and Dynkin diagrams correspond to and are used to classify root systems and therefore semisimple Lie algebras. Description A Coxeter group is a group that admits a presentation: \langle r_0,r_1,\dots,r_n \mid (r_i r_j)^ = 1 \rangle where the are integers that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold
In the mathematical disciplines of topology and geometry, an orbifold (for "orbit-manifold") is a generalization of a manifold. Roughly speaking, an orbifold is a topological space that is locally a finite group quotient of a Euclidean space. Definitions of orbifold have been given several times: by Ichirō Satake in the context of automorphic forms in the 1950s under the name ''V-manifold''; by William Thurston in the context of the geometry of 3-manifolds in the 1970s when he coined the name ''orbifold'', after a vote by his students; and by André Haefliger in the 1980s in the context of Mikhail Gromov's programme on CAT(k) spaces under the name ''orbihedron''. Historically, orbifolds arose first as surfaces with singular points long before they were formally defined. One of the first classical examples arose in the theory of modular forms with the action of the modular group \mathrm(2,\Z) on the upper half-plane: a version of the Riemann–Roch theorem holds after the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loop (graph Theory)
In graph theory, a loop (also called a self-loop or a ''buckle'') is an edge that connects a vertex to itself. A simple graph contains no loops. Depending on the context, a graph or a multigraph may be defined so as to either allow or disallow the presence of loops (often in concert with allowing or disallowing multiple edges between the same vertices): * Where graphs are defined so as to ''allow'' loops and multiple edges, a graph without loops or multiple edges is often distinguished from other graphs by calling it a ''simple graph''. * Where graphs are defined so as to ''disallow'' loops and multiple edges, a graph that does have loops or multiple edges is often distinguished from the graphs that satisfy these constraints by calling it a ''multigraph'' or ''pseudograph''. In a graph with one vertex, all edges must be loops. Such a graph is called a bouquet. Degree For an undirected graph, the degree of a vertex is equal to the number of adjacent vertices. A special ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |