|
Gompertz Constant
In mathematics, the Gompertz constant or Euler–Gompertz constant, denoted by \delta, appears in integral evaluations and as a value of special functions. It is named after Benjamin Gompertz. It can be defined by the continued fraction : \delta = \frac , or, alternatively, by : \delta = 1-\frac or : \delta = \frac. The most frequent appearance of \delta is in the following integrals: : \delta = \int_0^\infty\ln(1+x)e^dx=\int_0^\infty\fracdx=\int_0^1\fracdx. The first integral defines \delta, and the second and third follow from an integration of parts and a variable substitution respectively. The numerical value of \delta is about : \delta = 0.596347362323194074341078499369279376074\dots When Euler studied divergent infinite series, he encountered \delta via, for example, the above integral representations. Le Lionnais called \delta the Gompertz constant because of its role in survival analysis. In 2009 Alexander Aptekarev proved that at least one of the Euler–M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Function
Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other applications. The term is defined by consensus, and thus lacks a general formal definition, but the List of mathematical functions contains functions that are commonly accepted as special. Tables of special functions Many special functions appear as solutions of differential equations or integrals of elementary functions. Therefore, tables of integrals usually include descriptions of special functions, and tables of special functions include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie groups and Lie algebras, as well as certain topics in mathematical physics. Sy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
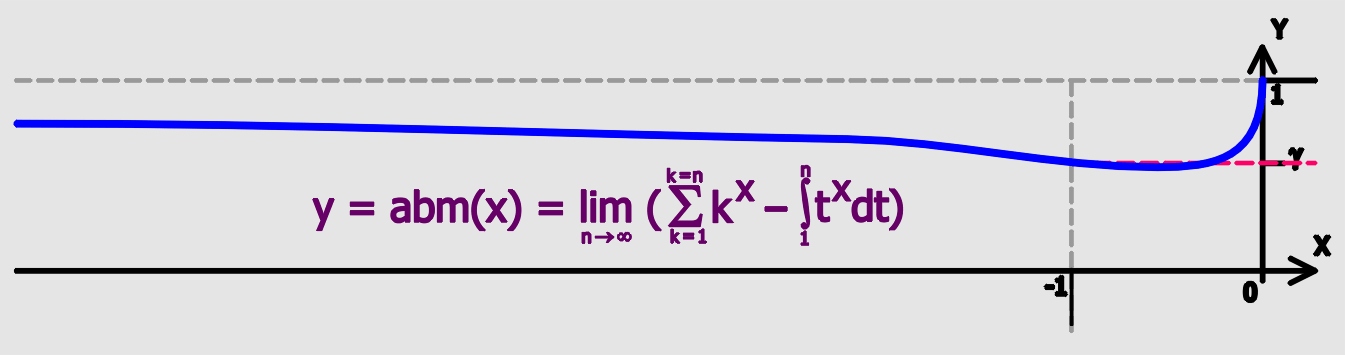
Benjamin Gompertz
Benjamin Gompertz (5 March 1779 – 14 July 1865) was a British self-educated mathematician and actuary, who became a Fellow of the Royal Society. Gompertz is now best known for his Gompertz law of mortality, a demographic model published in 1825. He was the brother of the early animal rights activist and inventor Lewis Gompertz and the poet Isaac Gompertz. Life Of the German Jewish family of Gompertz of Emmerich, he was born in London, where his father and grandfather had been successful diamond merchants. Debarred, as a Jew, from a university education, he studied on his own from an early age, in the writings of Isaac Newton, Colin Maclaurin, and William Emerson. From 1798 he was a prominent contributor to the ''Gentleman's Mathematical Companion'', and for a period won the annual prizes in the magazine for the solutions of problems. Gompertz married Abigail Montefiore (1790–1871) in 1810; they had three children. In line with his father's wishes, he entered the London St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continued Fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. It is generally assumed that the numerator of all of the fractions is 1. If arbitrary values and/or functions are used in place of one or more of the numerators or the integers in the denominators, the resulting expression is a generalized continued fraction. When it is ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
François Le Lionnais
François Le Lionnais (3 October 1901 – 13 March 1984) was a French chemical engineer and writer. He was a co-founder of the literary movement Oulipo. Biography Le Lionnais was born in Paris on 3 October 1901. Trained as a chemical engineer, he directed the Forges d'Aquiny industrial firm during the years 1928–1929. Active in the French resistance group Front National during World War II, he was arrested and tortured by the Gestapo in October 1944 and spent six months (November 1944 – April 1945) as a prisoner in the Dora concentration camp. His 1946 essay “La Peinture à Dora” (“Painting in Dora”) describes his experience as a prisoner. After World War II, Le Lionnais became the director of General Studies at the École Supérieure de Guerre (now part of the École Militaire). In 1950, he became the founding head of the Division of Science Education at UNESCO. Together with the French physicist Louis de Broglie and his close friend Jacques Bergier, Le Lio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gompertz Function
The Gompertz curve or Gompertz function is a type of mathematical model for a time series, named after Benjamin Gompertz (1779–1865). It is a sigmoid function which describes growth as being slowest at the start and end of a given time period. The right-side or future value asymptote of the function is approached much more gradually by the curve than the left-side or lower valued asymptote. This is in contrast to the simple logistic function in which both asymptotes are approached by the curve symmetrically. It is a special case of the generalised logistic function. The function was originally designed to describe human mortality, but since has been modified to be applied in biology, with regard to detailing populations. History Benjamin Gompertz (1779–1865) was an actuary in London who was privately educated. He was elected a fellow of the Royal Society in 1819. The function was first presented in his June 16, 1825 paper at the bottom of page 518. The Gompertz function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and . Though only a few classes of transcendental numbers are known—partly because it can be extremely difficult to show that a given number is transcendental—transcendental numbers are not rare. Indeed, almost all real and complex numbers are transcendental, since the algebraic numbers comprise a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic. The converse is not true: not all irrational numbers are transcendental. Hence, the set of real numbers consists of non-overlapping rational, alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Integral
In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument. Definitions For real non-zero values of ''x'', the exponential integral Ei(''x'') is defined as : \operatorname(x) = -\int_^\infty \fract\,dt = \int_^x \fract\,dt. The Risch algorithm shows that Ei is not an elementary function. The definition above can be used for positive values of ''x'', but the integral has to be understood in terms of the Cauchy principal value due to the singularity of the integrand at zero. For complex values of the argument, the definition becomes ambiguous due to branch points at 0 and Instead of Ei, the following notation is used, :E_1(z) = \int_z^\infty \frac\, dt,\qquad, (z), 0. Properties Several properties of the exponential integral below, in certain cases, allow one to avoid its explicit evaluation through the definition above. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gregory Coefficients
Gregory coefficients , also known as reciprocal logarithmic numbers, Bernoulli numbers of the second kind, or Cauchy numbers of the first kind,Ch. Jordan. ''The Calculus of Finite Differences'' Chelsea Publishing Company, USA, 1947.L. Comtet. ''Advanced combinatorics (2nd Edn.)'' D. Reidel Publishing Company, Boston, USA, 1974. are the rational numbers that occur in the Maclaurin series expansion of the reciprocal logarithm : \begin \frac & = 1+\frac12 z - \fracz^2 + \fracz^3 - \fracz^4 + \fracz^5 - \fracz^6 + \cdots \\ & = 1 + \sum_^\infty G_n z^n\,,\qquad , z, <1\,. \end Gregory coefficients are alternating and decreasing in absolute value. These numbers are named after James Gregory who introduced them in 1670 in the numerical integration context. They were subsequently rediscovered by many mathematicians and often appear in works of modern autho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |