|
Glivenko
Valery Ivanovich Glivenko (, ; 2 January 1897 (Gregorian calendar) / 21 December 1896 (Julian calendar) in Kyiv – 15 February 1940 in Moscow) was a Soviet mathematician. He worked in the foundations of mathematics, real analysis, probability theory, and mathematical statistics. He taught at the Moscow Industrial Pedagogical Institute until his death at age 43. Most of Glivenko's work was published in French. See also * Glivenko's double-negation translation * Glivenko's theorem (probability theory) *Glivenko–Cantelli theorem In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the fundamental theorem of statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, describes the asymptotic behaviour of the empirica ... * Glivenko–Stone theorem Notes Works * * * * * * * * External links * Photograph Mathematical logicians 1896 births 1940 deaths Soviet logicians Soviet mathematicians Ukrainian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko–Cantelli Theorem
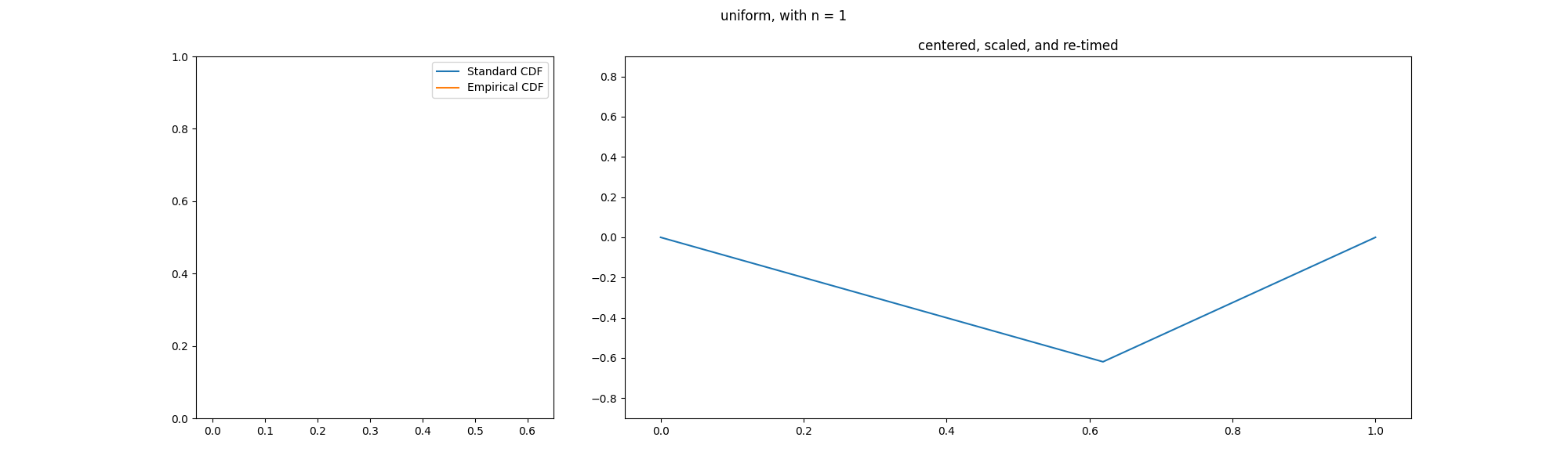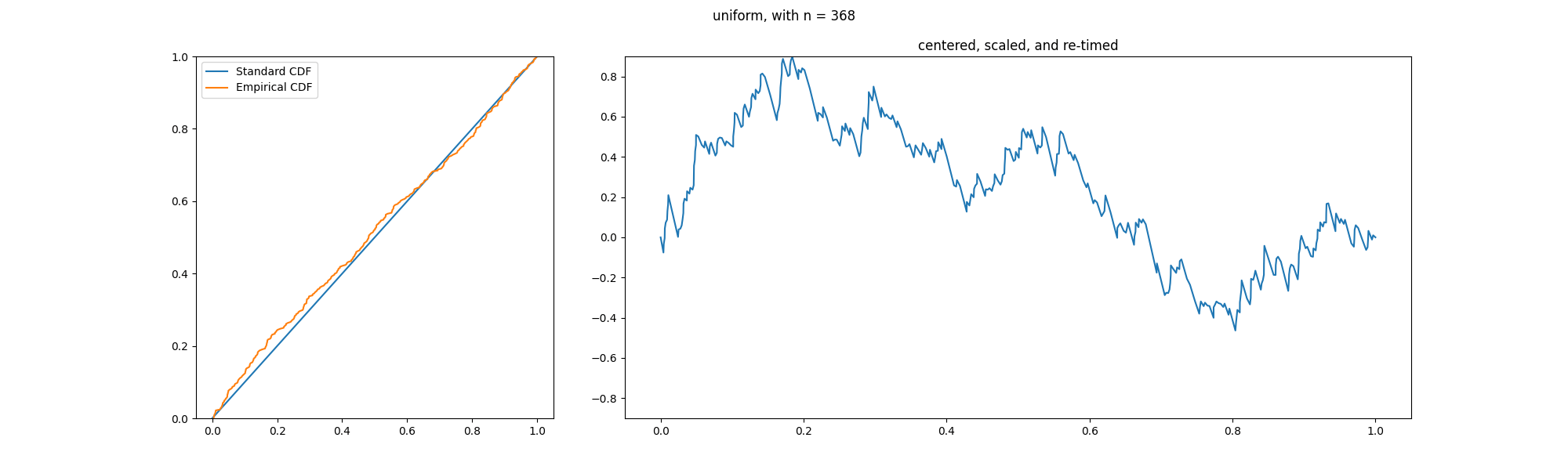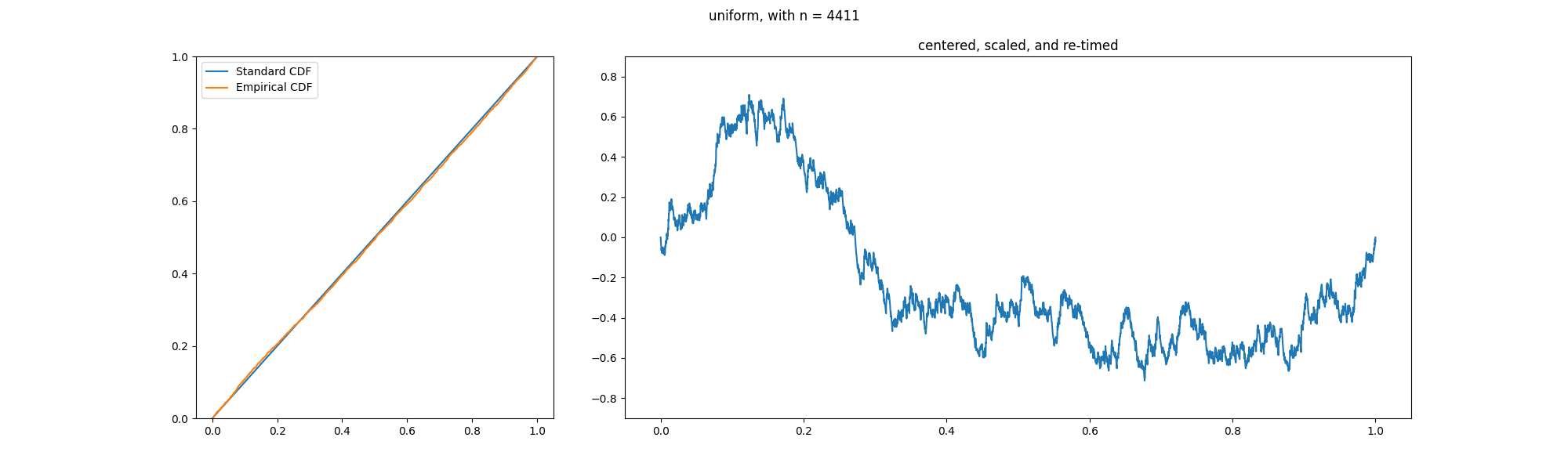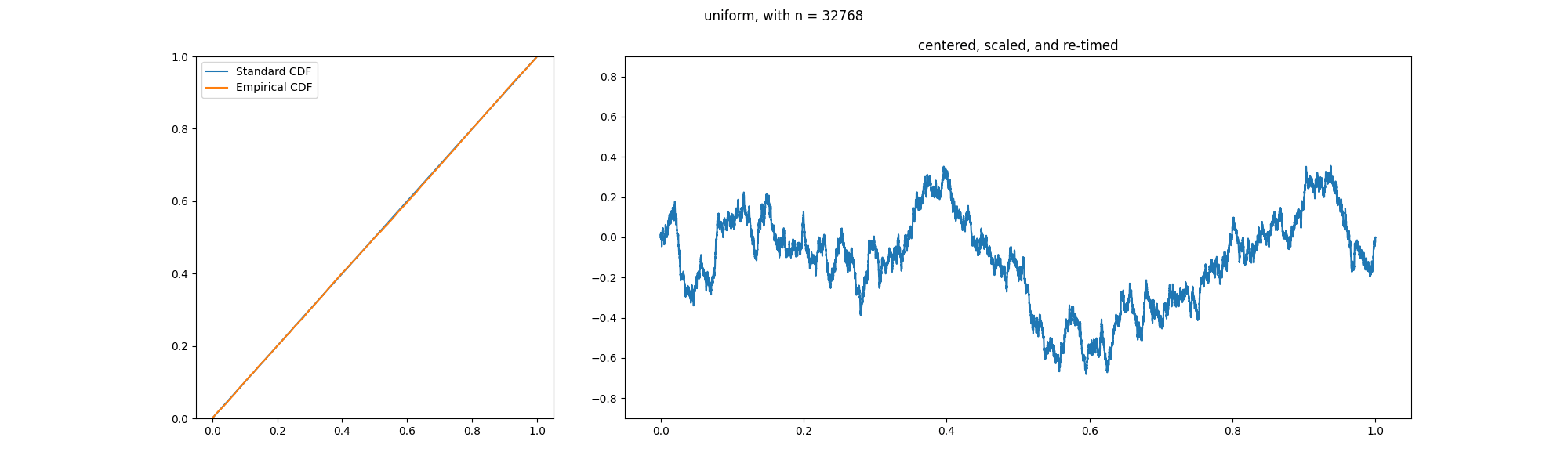
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the fundamental theorem of statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, describes the asymptotic behaviour of the empirical distribution function as the number of Independent and identically distributed random variables, independent and identically distributed observations grows. Specifically, the empirical distribution function Uniform convergence, converges uniformly to the true distribution function almost surely. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with commo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double-negation Translation
In proof theory, a discipline within mathematical logic, double-negation translation, sometimes called negative translation, is a general approach for embedding classical logic into intuitionistic logic. Typically it is done by translating formulas to formulas that are classically equivalent but intuitionistically inequivalent. Particular instances of double-negation translations include Glivenko's translation for propositional logic, and the Gödel–Gentzen translation and Kuroda's translation for first-order logic. Propositional logic The easiest double-negation translation to describe comes from Glivenko's theorem, proved by Valery Glivenko in 1929. It maps each classical formula φ to its double negation ¬¬φ. Glivenko's theorem states: :If φ is a propositional formula, then φ is a classical tautology if and only if ¬¬φ is an intuitionistic tautology. Glivenko's theorem implies the more general statement: :If ''T'' is a set of propositional formulas and φ a proposi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko's Theorem (probability Theory)
In probability theory, Glivenko's theorem states that if \varphi_n, n\in \mathbb N, \varphi are the characteristic functions of some probability distribution In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...s \mu_n, \mu respectively and \varphi_n \to \varphi almost everywhere, then \mu_n \to \mu in the sense of probability distributions. References Theory of probability distributions Theorems in probability theory {{probability-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kyiv
Kyiv, also Kiev, is the capital and most populous List of cities in Ukraine, city of Ukraine. Located in the north-central part of the country, it straddles both sides of the Dnieper, Dnieper River. As of 1 January 2022, its population was 2,952,301, making Kyiv the List of European cities by population within city limits, seventh-most populous city in Europe. Kyiv is an important industrial, scientific, educational, and cultural center. It is home to many High tech, high-tech industries, higher education institutions, and historical landmarks. The city has an extensive system of Transport in Kyiv, public transport and infrastructure, including the Kyiv Metro. The city's name is said to derive from the name of Kyi, one of its four legendary founders. During History of Kyiv, its history, Kyiv, one of the oldest cities in Eastern Europe, passed through several stages of prominence and obscurity. The city probably existed as a commercial center as early as the 5th century. A Slav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theorists
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th ed., (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', vol. 1, 3rd ed., (1968), Wiley, . This number is often expressed as a percentage (%), ranging from 0% to 100%. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These concepts have been given an axiomatic mathematical formaliza ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ukrainian Mathematicians
This is a list of the best known Ukraine, Ukrainian mathematicians. This list includes some Poland, Polish, Russian Empire, pre-revolutionary Russian and USSR, Soviet mathematicians who lived or worked in Ukraine. __NOTOC__ {{compact ToC, side=yes, top=yes, num=yes A * Naum Akhiezer, Akhiezer, Naum Ilyich (1901–1980) B * Sergei Natanovich Bernstein, Bernstein, Sergei Natanovich (1880–1968) * Valentina Borok, Borok, Valentina Mikhailovna (1931–2004) * Leonid Berlyand, Berlyand, Leonid Viktorovich (b. 1957) D * Vladimir Drinfeld, Drinfeld, Volodymyr Gershonovych (b. 1954) E * Alexandre Eremenko, Eremenko, Oleksandr Emmanuilovich (b. 1954) G * Yakov Geronimus, Geronimus, Yakov Lazarevich (1898–1984) * Victor Glushkov, Glushkov, Victor Mihailovich (1923–1982) * Anatolii Goldberg, Goldberg, Anatolii Asirovich (1930–2008) * Dmitry Grave, Grave, Dmytro Olexandrovych (1863–1939) K * Mikhail Kadets, Kadets, Mikhail Iosiphovich (1923–2011) * Volodymyr Korolyu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soviet Mathematicians
This list of Russian mathematicians includes the famous mathematicians from the Russian Empire, the Soviet Union and the Russian Federation. Alphabetical list __NOTOC__ A *Georgy Adelson-Velsky, inventor of AVL tree algorithm, developer of Kaissa, the first world computer chess champion *Sergei Adian, known for his work in group theory, especially on the Burnside problem *Aleksandr Danilovich Aleksandrov, Aleksandr Aleksandrov, developer of CAT(k) space and Alexandrov's uniqueness theorem in geometry *Pavel Alexandrov, author of the Alexandroff compactification and the Alexandrov topology *Dmitri Anosov, developed Anosov diffeomorphism *Vladimir Arnold, an author of the Kolmogorov–Arnold–Moser theorem in dynamical systems, solved Hilbert's 13th problem, raised the ADE classification and Arnold's rouble problems B *Alexander Beilinson, influential mathematician in representation theory, algebraic geometry and mathematical physics *Sergey Bernstein, developed the Bernstein p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soviet Logicians
The Union of Soviet Socialist Republics. (USSR), commonly known as the Soviet Union, was a transcontinental country that spanned much of Eurasia from 1922 until it dissolved in 1991. During its existence, it was the largest country by area, extending across eleven time zones and sharing borders with twelve countries, and the third-most populous country. An overall successor to the Russian Empire, it was nominally organized as a federal union of national republics, the largest and most populous of which was the Russian SFSR. In practice, its government and economy were highly centralized. As a one-party state governed by the Communist Party of the Soviet Union (CPSU), it was a flagship communist state. Its capital and largest city was Moscow. The Soviet Union's roots lay in the October Revolution of 1917. The new government, led by Vladimir Lenin, established the Russian SFSR, the world's first constitutionally communist state. The revolution was not accepted by all wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1940 Deaths
A calendar from 1940 according to the Gregorian calendar, factoring in the dates of Easter and related holidays, cannot be used again until the year 5280. Events Below, events related to World War II have the "WWII" prefix. January *January 4 – WWII: Luftwaffe Chief and Generalfeldmarschall Hermann Göring assumes control of most war industries in Nazi Germany, Germany, in his capacity as Plenipotentiary for the Four Year Plan. *January 6 – WWII: Winter War – General Semyon Timoshenko takes command of all Soviet forces. *January 7 – WWII: Winter War: Battle of Raate Road – Outnumbered Finnish troops decisively defeat Soviet forces. *January 8 – WWII: **Winter War: Battle of Suomussalmi – Finnish forces destroy the 44th Rifle Division (Soviet Union), Soviet 44th Rifle Division. **Food rationing in the United Kingdom begins; it will remain in force until 1954. *January 9 – WWII: British submarine is sunk in the Heligoland Bight. *January 10 – WWII: Mechele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1896 Births
Events January * January 2 – The Jameson Raid comes to an end as Jameson surrenders to the Boers. * January 4 – Utah is admitted as the 45th U.S. state. * January 5 – An Austrian newspaper reports Wilhelm Röntgen's discovery, last November, of a type of electromagnetic radiation, later known as X-rays. * January 6 – Cecil Rhodes is forced to resign as Prime Minister of the Cape Colony, Cape of Good Hope for his involvement in the Jameson Raid. * January 7 – American culinary expert Fannie Farmer publishes her first cookbook. * January 12 – H. L. Smith takes the first X-ray photograph. * January 16 – Devonport High School for Boys is founded in Plymouth (England). * January 17 – Anglo-Ashanti wars#Fourth Anglo-Ashanti War (1895–1896), Fourth Anglo-Ashanti War: British British Army, redcoats enter the Ashanti people, Ashanti capital, Kumasi, and Asantehene Agyeman Prempeh I is deposed. * January 28 – Walter Arnold, of E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logicians
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a ''proof'' consisting of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstractio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |