|
Geometric Separator
A geometric separator is a line (or another shape) that partitions a collection of geometric shapes into two subsets, such that proportion of shapes in each subset is bounded, and the number of shapes that do not belong to any subset (i.e. the shapes intersected by the separator itself) is small. When a geometric separator exists, it can be used for building divide-and-conquer algorithms for solving various problems in computational geometry. Separators that are lines General question In 1979, Helge Tverberg raised the following question. For two positive integers ''k'', ''l'', what is the smallest number ''n''(''k'',''l'') such that, for any family of pairwise-disjoint convex objects in the plane, there exists a straight line that has at least ''k'' objects on one side and at least ''l'' on the other side? The following results are known. * Obviously, ''n''(1,1)=1. * Hope and Katchalski proved that ''n''(''k'',1) ≤ 12(''k''-1) for all ''k'' ≥ 2. * Villanger prov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helly's Theorem
Helly's theorem is a basic result in discrete geometry on the intersection of convex sets. It was discovered by Eduard Helly in 1913,. but not published by him until 1923, by which time alternative proofs by and had already appeared. Helly's theorem gave rise to the notion of a Helly family. Statement Let be a finite collection of convex subsets of \R^d, with n\geq d+1. If the intersection of every d+1 of these sets is nonempty, then the whole collection has a nonempty intersection; that is, :\bigcap_^n X_j\ne\varnothing. For infinite collections one has to assume compactness: Let \ be a collection of compact convex subsets of \R^d, such that every subcollection of cardinality at most d+1 has nonempty intersection. Then the whole collection has nonempty intersection. Proof We prove the finite version, using Radon's theorem as in the proof by . The infinite version then follows by the finite intersection property characterization of compactness: a collection of closed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Theorem (other)
Separation theorem may refer to several theorems in different fields. Economics * Fisher separation theorem (corporation theory) - asserts that the objective of a corporation will be the maximization of its present value, regardless of the preferences of its shareholders. *Mutual fund separation theorem (portfolio theory) states that, under certain conditions, any investor's optimal portfolio can be constructed by holding each of certain mutual funds in appropriate ratios, where the number of mutual funds is smaller than the number of individual assets in the portfolio. Mathematics * Gabbay's separation theorem (mathematical logic and computer science) states that any arbitrary temporal logic formula can be rewritten in a logically equivalent "past → future" form. * Planar separator theorem (graph theory) states that any planar graph can be split into smaller pieces by removing a small number of vertices. * Lusin's separation theorem (descriptive set theory) states that for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guillotine Separation
Guillotine cutting is the process of producing small rectangular items of fixed dimensions from a given large rectangular sheet, using only guillotine-cuts. A guillotine-cut (also called an edge-to-edge cut) is a straight bisecting line going from one edge of an existing rectangle to the opposite edge, similarly to a paper guillotine. Guillotine cutting is particularly common in the glass industry. Glass sheets are scored along horizontal and vertical lines, and then broken along these lines to obtain smaller panels. It is also useful for cutting steel plates, cutting of wood sheets to make furniture, and cutting of cardboard into boxes. There are various optimization problems related to guillotine cutting, such as: maximize the total area of the produced pieces, or their total value; minimize the amount of waste (unused parts) of the large sheet, or the total number of sheets. They have been studied in combinatorial geometry, operations research and industrial engineering. A r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ham Sandwich Theorem
In mathematical measure theory, for every positive integer the ham sandwich theorem states that given measurable "objects" in -dimensional Euclidean space, it is possible to divide each one of them in half (with respect to their Measure (mathematics), measure, e.g. volume) with a single -dimensional hyperplane. This is possible even if the objects overlap. It was proposed by Hugo Steinhaus and proved by Stefan Banach (explicitly in dimension 3, without stating the theorem in the -dimensional case), and also years later called the Stone–Tukey theorem after Arthur Harold Stone, Arthur H. Stone and John Tukey. Naming The ham sandwich theorem takes its name from the case when and the three objects to be bisected are the ingredients of a ham sandwich. Sources differ on whether these three ingredients are two slices of bread and a piece of ham , bread and cheese and ham , or bread and butter and ham . In two dimensions, the theorem is known as the pancake theorem to refer to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Contact Graph
In the mathematical area of graph theory, a contact graph or tangency graph is a graph whose vertices are represented by geometric objects (e.g. curves, line segments, or polygons), and whose edges correspond to two objects touching (but not crossing) according to some specified notion. It is similar to the notion of an intersection graph but differs from it in restricting the ways that the underlying objects are allowed to intersect each other. The circle packing theorem states that every planar graph can be represented as a contact graph of circles, known as a coin graph. The contact graphs of unit circles are called penny graphs. Representations as contact graphs of triangles, rectangles, squares, line segment In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special c ...s, or circular a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Packing Theorem
The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles (in general, on any Riemann surface) whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex (graph theory), vertex for each circle, and an edge (graph theory), edge for every pair of circles that are tangent circles, tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple graph, simple, and planar graph, planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph: Circle packing theorem: For every finite connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planar Separator Theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an -vertex graph (where the invokes big O notation) can partition the graph into disjoint subgraphs each of which has at most vertices. A weaker form of the separator theorem with vertices in the separator instead of was originally proven by , and the form with the tight asymptotic bound on the separator size was first proven by . Since their work, the separator theorem has been reproven in several different ways, the constant in the term of the theorem has been improved, and it has been extended to certain classes of nonplanar graphs. Repeated application of the separator theorem produces a separator hierarchy which may take the form of either a tree decomposition or a branch-decomposition of the graph. Separator hierarchi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Independent Set
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative'' extrema) or on the entire domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
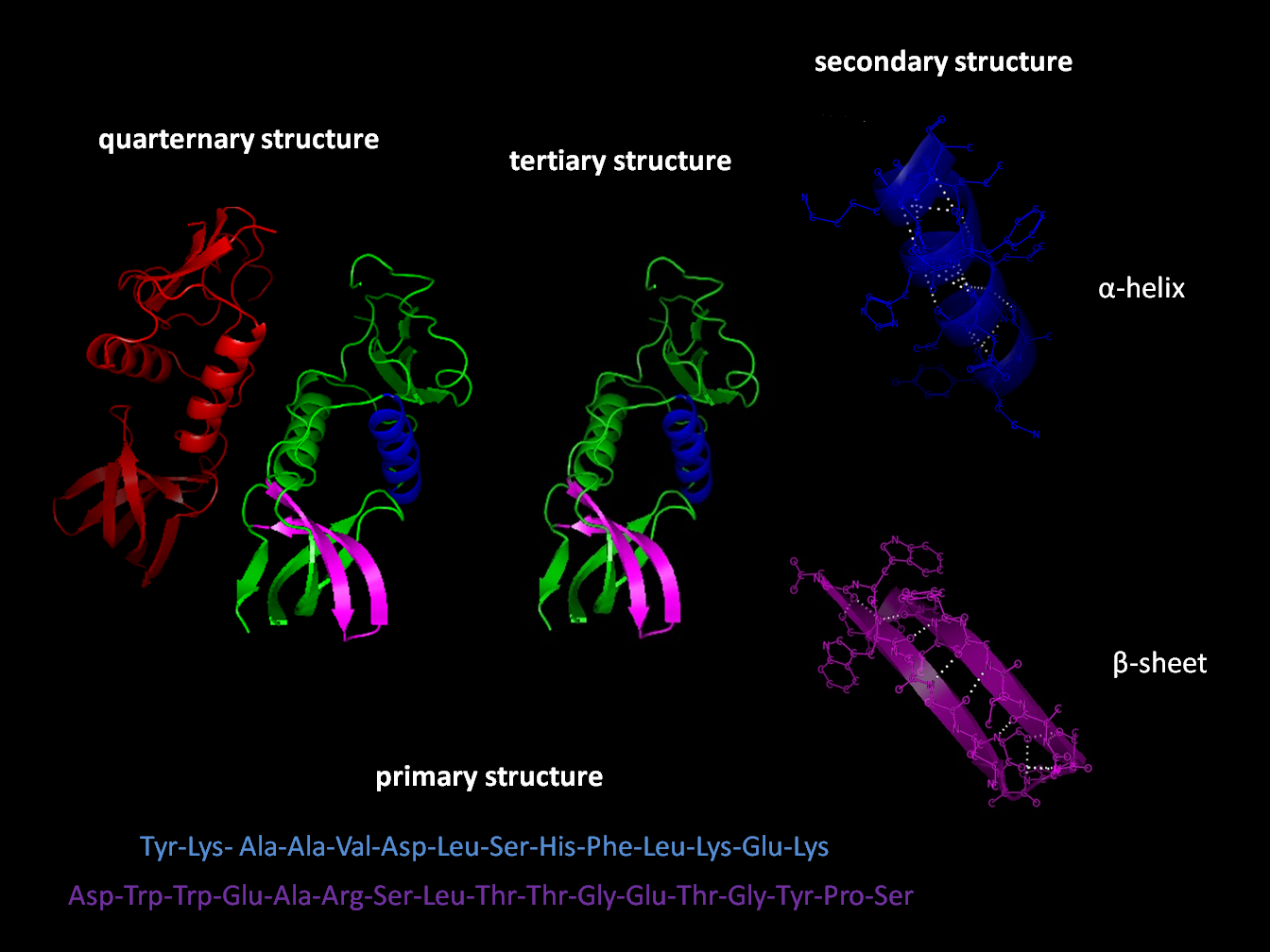
Protein Folding
Protein folding is the physical process by which a protein, after Protein biosynthesis, synthesis by a ribosome as a linear chain of Amino acid, amino acids, changes from an unstable random coil into a more ordered protein tertiary structure, three-dimensional structure. This structure permits the protein to become biologically functional or active. The folding of many proteins begins even during the translation of the polypeptide chain. The amino acids interact with each other to produce a well-defined three-dimensional structure, known as the protein's native state. This structure is determined by the amino-acid sequence or primary structure. The correct three-dimensional structure is essential to function, although some parts of functional proteins Intrinsically unstructured proteins, may remain unfolded, indicating that protein dynamics are important. Failure to fold into a native structure generally produces inactive proteins, but in some instances, misfolded proteins have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if \frac = \frac = \varphi, where the Greek letter Phi (letter), phi ( or ) denotes the golden ratio. The constant satisfies the quadratic equation and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli; it also goes by other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the Straightedge and compass construction, construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of —may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has bee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helge Tverberg
Helge Arnulf Tverberg (March 6, 1935December 28, 2020) was a Norwegian mathematician. He was a professor in the Mathematics Department at the University of Bergen, his speciality being combinatorics; he retired at the mandatory age of seventy. He was born in Bergen. He took the cand.real. degree at the University of Bergen in 1958, and the dr.philos. degree in 1968. He was a lecturer from 1958 to 1971 and professor from 1971 to his retirement in 2005. He was a visiting scholar at the University of Reading in 1966 and at the Australian National University, in Canberra, from 1980 to 1981, 1987 to 1988 and in 2004. He was a member of the Norwegian Academy of Science and Letters. Tverberg, in 1965, proved a result on intersection patterns of partitions of point configurations that has come to be known as Tverberg's partition theorem. It inaugurated a new branch of combinatorial geometry, with many variations and applications. An account by Günter M. Ziegler of Tverberg's work ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |