|
Genetic Correlation
In multivariate quantitative genetics, a genetic correlation (denoted r_g or r_a) is the proportion of variance that two traits share due to genetic causes, the correlation between the genetic influences on a trait and the genetic influences on a different trait#Plomin, Plomin et al., p. 123 estimating the degree of pleiotropy or causal overlap. A genetic correlation of 0 implies that the genetic effects on one trait are independent of the other, while a correlation of 1 implies that all of the genetic influences on the two traits are identical. The bivariate genetic correlation can be generalized to inferring genetic latent variable factors across > 2 traits using factor analysis. Genetic correlation models were introduced into behavioral genetics in the 1970s–1980s. Genetic correlations have applications in validation of genome-wide association study (GWAS) results, breeding, prediction of traits, and discovering the etiology of traits & diseases. They can be estimated usi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Heritability
Heritability is a statistic used in the fields of Animal husbandry, breeding and genetics that estimates the degree of ''variation'' in a phenotypic trait in a population that is due to genetic variation between individuals in that population. The concept of heritability can be expressed in the form of the following question: "What is the proportion of the variation in a given trait within a population that is ''not'' explained by the environment or random chance?" Other causes of measured variation in a trait are characterized as environment (biophysical), environmental factors, including observational error. In human studies of heritability these are often apportioned into factors from "shared environment" and "non-shared environment" based on whether they tend to result in persons brought up in the same household being more or less similar to persons who were not. Heritability is estimated by comparing individual phenotypic variation among related individuals in a population, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Intelligence
Intelligence has been defined in many ways: the capacity for abstraction, logic, understanding, self-awareness, learning, emotional knowledge, reasoning, planning, creativity, critical thinking, and problem-solving. It can be described as the ability to perceive or infer information and to retain it as knowledge to be applied to adaptive behaviors within an environment or context. The term rose to prominence during the early 1900s. Most psychologists believe that intelligence can be divided into various domains or competencies. Intelligence has been long-studied in humans, and across numerous disciplines. It has also been observed in the cognition of non-human animals. Some researchers have suggested that plants exhibit forms of intelligence, though this remains controversial. Etymology The word '' intelligence'' derives from the Latin nouns '' intelligentia'' or '' intellēctus'', which in turn stem from the verb '' intelligere'', to comprehend or perceive. In the M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Statistical Power
In frequentist statistics, power is the probability of detecting a given effect (if that effect actually exists) using a given test in a given context. In typical use, it is a function of the specific test that is used (including the choice of test statistic and significance level), the sample size (more data tends to provide more power), and the effect size (effects or correlations that are large relative to the variability of the data tend to provide more power). More formally, in the case of a simple hypothesis test with two hypotheses, the power of the test is the probability that the test correctly rejects the null hypothesis (H_0) when the alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, where \beta is the probability of making a type II error (a false negative) conditional on there being a true effect or association. Background Statistical testing uses data from samples to assess, or make inferences about, a statistical population. Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Prior Probability
A prior probability distribution of an uncertain quantity, simply called the prior, is its assumed probability distribution before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable. In Bayesian statistics, Bayes' rule prescribes how to update the prior with new information to obtain the posterior probability distribution, which is the conditional distribution of the uncertain quantity given new data. Historically, the choice of priors was often constrained to a conjugate family of a given likelihood function, so that it would result in a tractable posterior of the same family. The widespread availability of Markov chain Monte Carlo methods, however, has made this less of a concern. There are many ways to const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Polygenic Score
In genetics, a polygenic score (PGS) is a number that summarizes the estimated effect of many genetic variants on an individual's phenotype. The PGS is also called the polygenic index (PGI) or genome-wide score; in the context of disease risk, it is called a polygenic risk score (PRS or PR score) or genetic risk score. The score reflects an individual's estimated genetic predisposition for a given trait and can be used as a predictor for that trait. It gives an estimate of how likely an individual is to have a given trait based only on genetics, without taking environmental factors into account; and it is typically calculated as a weighted sum of trait-associated alleles. Recent progress in genetics has developed polygenic predictors of complex human traits, including risk for many important complex diseases that are typically affected by many genetic variants, each of which confers a small effect on overall risk. In a polygenic risk predictor the lifetime (or age-range) risk fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
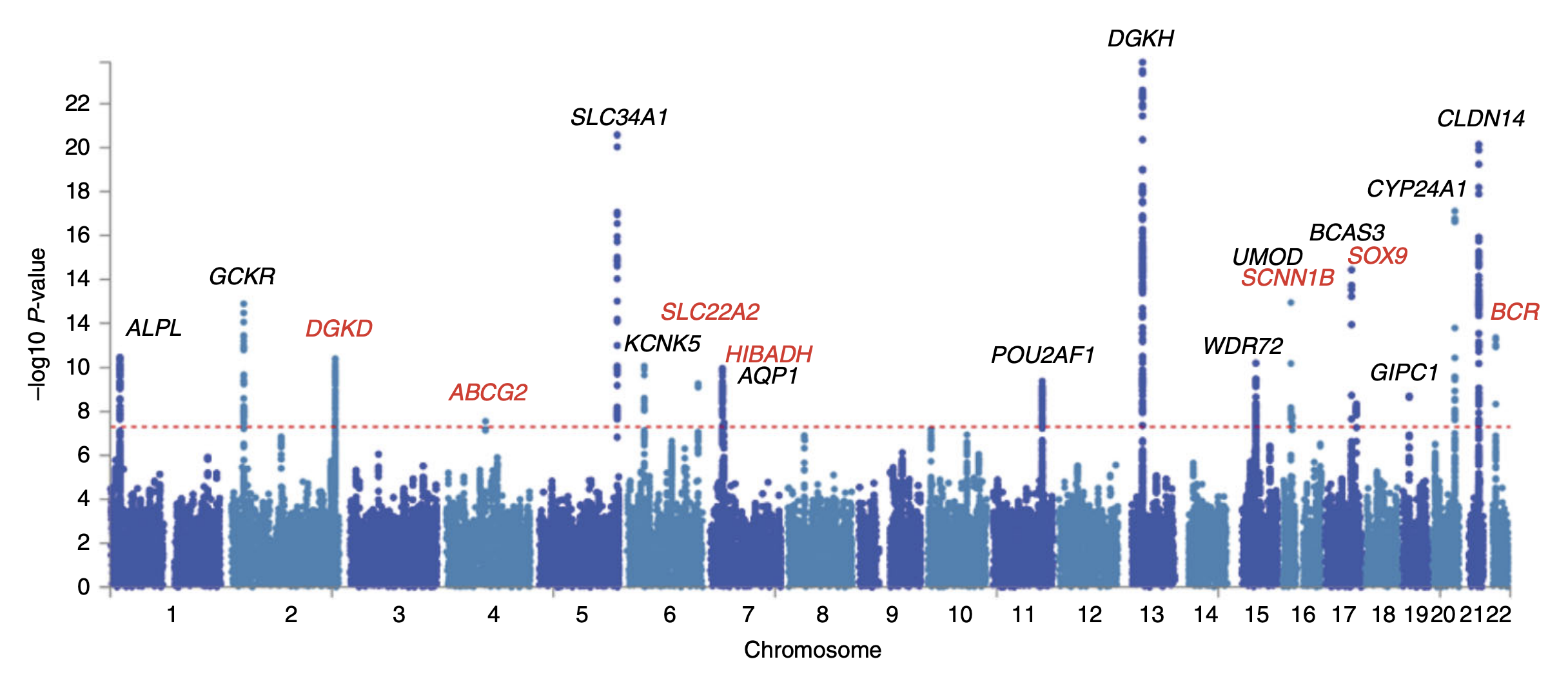 |
Genome-wide Association Study
In genomics, a genome-wide association study (GWA study, or GWAS), is an observational study of a genome-wide set of Single-nucleotide polymorphism, genetic variants in different individuals to see if any variant is associated with a trait. GWA studies typically focus on associations between single-nucleotide polymorphisms (SNPs) and traits like major human diseases, but can equally be applied to any other genetic variants and any other organisms. When applied to human data, GWA studies compare the DNA of participants having varying phenotypes for a particular trait or disease. These participants may be people with a disease (cases) and similar people without the disease (controls), or they may be people with different phenotypes for a particular trait, for example blood pressure. This approach is known as phenotype-first, in which the participants are classified first by their clinical manifestation(s), as opposed to Genotype-first approach, genotype-first. Each person gives a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Genetic Architecture
Genetic architecture is the underlying genetic basis of a phenotypic trait and its variational properties. Phenotypic variation for quantitative traits is, at the most basic level, the result of the segregation of alleles at quantitative trait loci (QTL). Environmental factors and other external influences can also play a role in phenotypic variation. Genetic architecture is a broad term that can be described for any given individual based on information regarding gene and allele number, the distribution of allelic and mutational effects, and patterns of pleiotropy, dominance, and epistasis. There are several different experimental views of genetic architecture. Some researchers recognize that the interplay of various genetic mechanisms is incredibly complex, but believe that these mechanisms can be averaged and treated, more or less, like statistical noise. Other researchers claim that each and every gene interaction is significant and that it is necessary to measure and model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Information Bias (epidemiology)
In epidemiology, information bias refers to bias arising from measurement error. Information bias is also referred to as observational bias and misclassification. ''A Dictionary of Epidemiology'', sponsored by the International Epidemiological Association, defines this as the following: "1. A flaw in measuring exposure, covariate, or outcome variables that results in different quality (accuracy) of information between comparison groups. The occurrence of information biases may not be independent of the occurrence of selection biases. 2. Bias in an estimate arising from measurement errors." Misclassification Misclassification thus refers to measurement error. There are two types of misclassification in epidemiological research: non-differential misclassification and differential misclassification. Nondifferential misclassification Nondifferential misclassification is when all classes, groups, or categories of a variable (whether exposure, outcome, or covariate) have the same ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Berkson's Paradox
Berkson's paradox, also known as Berkson's bias, collider bias, or Berkson's fallacy, is a result in conditional probability and statistics which is often found to be counterintuitive, and hence a veridical paradox. It is a complicating factor arising in statistical tests of proportions. Specifically, it arises when there is an ascertainment bias inherent in a study design. The effect is related to the explaining away phenomenon in Bayesian networks, and Collider (statistics), conditioning on a collider in graphical models. This paradox is often illustrated using scenarios from the fields of medical statistics or biostatistics, as in the original description of the problem by Joseph Berkson. Examples Overview The most common example of Berkson's paradox is a false observation of a ''negative'' correlation between two desirable traits, i.e., that members of a population which have some desirable traits tend to lack a second. Berkson's paradox occurs when this observation appe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Ascertainment Bias
In statistics, sampling bias is a bias (statistics), bias in which a sample is collected in such a way that some members of the intended statistical population, population have a lower or higher sampling probability than others. It results in a biased sample of a population (or non-human factors) in which all individuals, or instances, were not equally likely to have been selected. If this is not accounted for, results can be erroneously attributed to the phenomenon under study rather than to the method of sampling (statistics), sampling. Medical sources sometimes refer to sampling bias as ascertainment bias. Ascertainment bias has basically the same definition, but is still sometimes classified as a separate type of bias. Distinction from selection bias Sampling bias is usually classified as a subtype of selection bias, sometimes specifically termed sample selection bias, but some classify it as a separate type of bias. A distinction, albeit not universally accepted, of samplin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Population Stratification
Population structure (also called genetic structure and population stratification) is the presence of a systematic difference in allele frequencies between subpopulations. In a randomly mating (or ''panmictic'') population, allele frequencies are expected to be roughly similar between groups. However, mating tends to be non-random to some degree, causing structure to arise. For example, a barrier like a river can separate two groups of the same species and make it difficult for potential mates to cross; if a mutation occurs, over many generations it can spread and become common in one subpopulation while being completely absent in the other. Genetic variants do not necessarily cause observable changes in organisms, but can be correlated by coincidence because of population structure—a variant that is common in a population that has a high rate of disease may erroneously be thought to cause the disease. For this reason, population structure is a common confounding variable in m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |