|
Gauss Continued Fraction
In complex analysis, Gauss's continued fraction is a particular class of continued fractions derived from hypergeometric functions. It was one of the first analytic continued fractions known to mathematics, and it can be used to represent several important elementary functions, as well as some of the more complicated transcendental functions. History Lambert published several examples of continued fractions in this form in 1768, and both Euler and Lagrange investigated similar constructions, but it was Carl Friedrich Gauss who utilized the algebra described in the next section to deduce the general form of this continued fraction, in 1813. Although Gauss gave the form of this continued fraction, he did not give a proof of its convergence properties. Bernhard Riemann and L.W. Thomé obtained partial results, but the final word on the region in which this continued fraction converges was not given until 1901, by Edward Burr Van Vleck. Derivation Let f_0, f_1, f_2, \dots be a sequenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable, that is, '' holomorphic functions''. The concept can be extended to functions of several complex variables. Complex analysis is contrasted with real analysis, which dea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proof That π Is Irrational
In the 1760s, Johann Heinrich Lambert was the first to prove that the number is irrational, meaning it cannot be expressed as a fraction a/b, where a and b are both integers. In the 19th century, Charles Hermite found a proof that requires no prerequisite knowledge beyond basic calculus. Three simplifications of Hermite's proof are due to Mary Cartwright, Ivan Niven, and Nicolas Bourbaki. Another proof, which is a simplification of Lambert's proof, is due to Miklós Laczkovich. Many of these are proofs by contradiction. In 1882, Ferdinand von Lindemann proved that \pi is not just irrational, but transcendental as well. Lambert's proof In 1761, Johann Heinrich Lambert proved that \pi is irrational by first showing that this continued fraction expansion holds: :\tan(x) = \cfrac. Then Lambert proved that if x is non-zero and rational, then this expression must be irrational. Since \tan\tfrac\pi4 =1, it follows that \tfrac\pi4 is irrational, and thus \pi is also irrational. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Series
In mathematics, the binomial series is a generalization of the binomial formula to cases where the exponent is not a positive integer: where \alpha is any complex number, and the power series on the right-hand side is expressed in terms of the (generalized) binomial coefficients :\binom = \frac. The binomial series is the MacLaurin series for the function f(x)=(1+x)^\alpha. It converges when , x, - 1 is assumed. On the other hand, the series does not converge if , x, =1 and \operatorname(\alpha) \le - 1 , again by formula (). Alternatively, we may observe that for all j, \left, \fracj - 1 \ \ge 1 - \fracj \ge 1 . Thus, by formula (), for all k, \left, \ \ge 1 . This completes the proof of (iii). Turning to (iv), we use identity () above with x=-1 and \alpha-1 in place of \alpha, along with formula (), to obtain :\sum_^n \! (-1)^k = \! (-1)^n= \frac1 (1+o(1)) as n\to\infty. Assertion (iv) now follows from the asymptotic behavior of the sequence n^ = e^. (Precisely, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Trigonometric Functions
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted Domain of a function, domains. Specifically, they are the inverses of the sine, cosine, tangent (trigonometry), tangent, cotangent, secant (trigonometry), secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of radians will correspond to an circular arc, arc whose length is , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the exponentiation, power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the Integral, area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch Point
In the mathematical field of complex analysis, a branch point of a multivalued function is a point such that if the function is n-valued (has n values) at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept. Branch points fall into three broad categories: algebraic branch points, transcendental branch points, and logarithmic branch points. Algebraic branch points most commonly arise from functions in which there is an ambiguity in the extraction of a root, such as solving the equation w^2=z for w as a function of z. Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will result in a different function: there is non-trivial monodromy. Despite the algebraic branch point, the function w is well-defined as a multiple-valued function and, in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Trigonometric Functions
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted Domain of a function, domains. Specifically, they are the inverses of the sine, cosine, tangent (trigonometry), tangent, cotangent, secant (trigonometry), secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of radians will correspond to an circular arc, arc whose length is , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Padé Table
In complex analysis, a Padé table is an array, possibly of infinite extent, of the rational Padé approximants :''R''''m'', ''n'' to a given complex formal power series. Certain sequences of approximants lying within a Padé table can often be shown to correspond with successive convergents of a continued fraction representation of a holomorphic or meromorphic function. History Although earlier mathematicians had obtained sporadic results involving sequences of rational approximations to transcendental functions, Frobenius (in 1881) was apparently the first to organize the approximants in the form of a table. Henri Padé further expanded this notion in his doctoral thesis ''Sur la representation approchee d'une fonction par des fractions rationelles'', in 1892. Over the ensuing 16 years Padé published 28 additional papers exploring the properties of his table, and relating the table to analytic continued fractions. Modern interest in Padé tables was revived by H. S. Wall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Gamma Function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, which are defined similarly to the gamma function but with different or "incomplete" integral limits. The gamma function is defined as an integral from zero to infinity. This contrasts with the lower incomplete gamma function, which is defined as an integral from zero to a variable upper limit. Similarly, the upper incomplete gamma function is defined as an integral from a variable lower limit to infinity. Definition The upper incomplete gamma function is defined as: \Gamma(s,x) = \int_x^ t^\,e^\, dt , whereas the lower incomplete gamma function is defined as: \gamma(s,x) = \int_0^x t^\,e^\, dt . In both cases is a complex parameter, such that the real part of is positive. Properties By integration by parts we find the recurrence relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dawson Function
In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson) is the one-sided Fourier–Laplace sine transform of the Gaussian function. Definition The Dawson function is defined as either: D_+(x) = e^ \int_0^x e^\,dt, also denoted as F(x) or D(x), or alternatively D_-(x) = e^ \int_0^x e^\,dt.\! The Dawson function is the one-sided Fourier–Laplace sine transform of the Gaussian function, D_+(x) = \frac12 \int_0^\infty e^\,\sin(xt)\,dt. It is closely related to the error function erf, as : D_+(x) = e^ \operatorname (x) = - e^ \operatorname (ix) where erfi is the imaginary error function, Similarly, D_-(x) = \frac e^ \operatorname(x) in terms of the real error function, erf. In terms of either erfi or the Faddeeva function w(z), the Dawson function can be extended to the entire complex plane:Mofreh R. Zaghloul and Ahmed N. Ali,Algorithm 916: Computing the Faddeyeva and Voigt Functions" ''ACM Trans. Math. Soft.'' 38 (2), 15 (2011). Preprint availa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
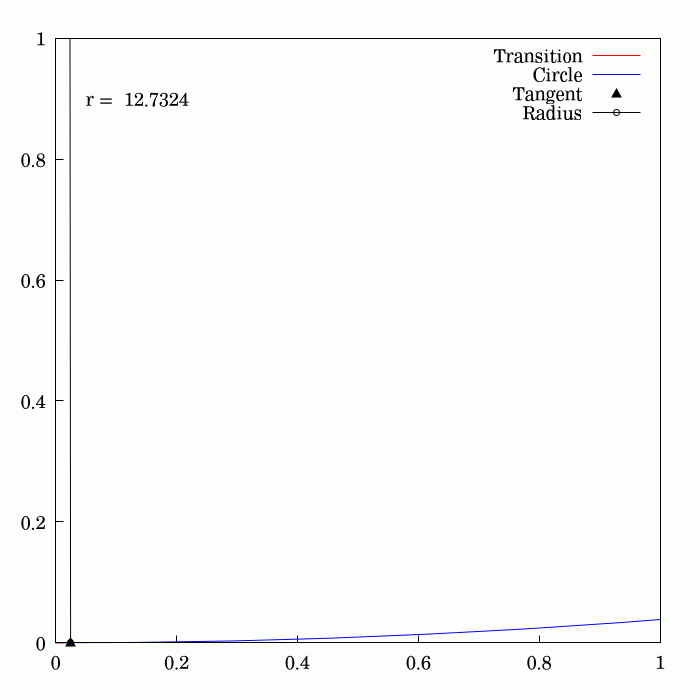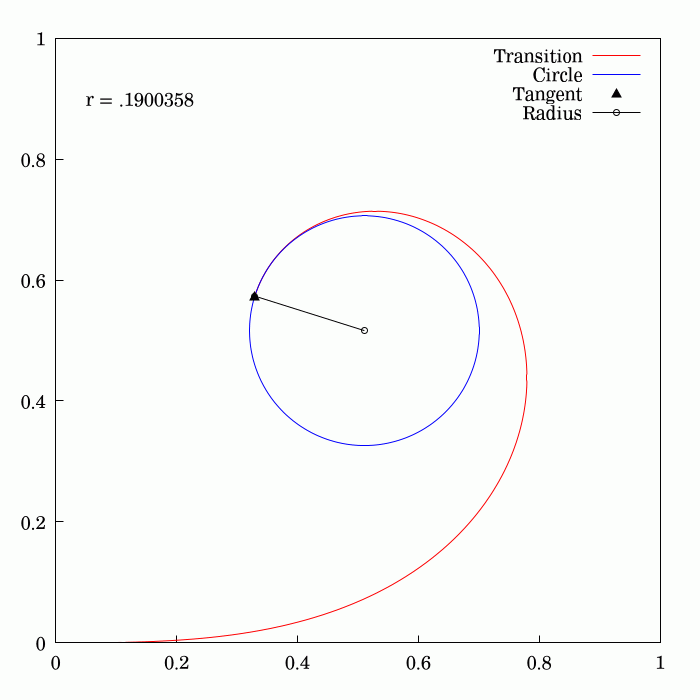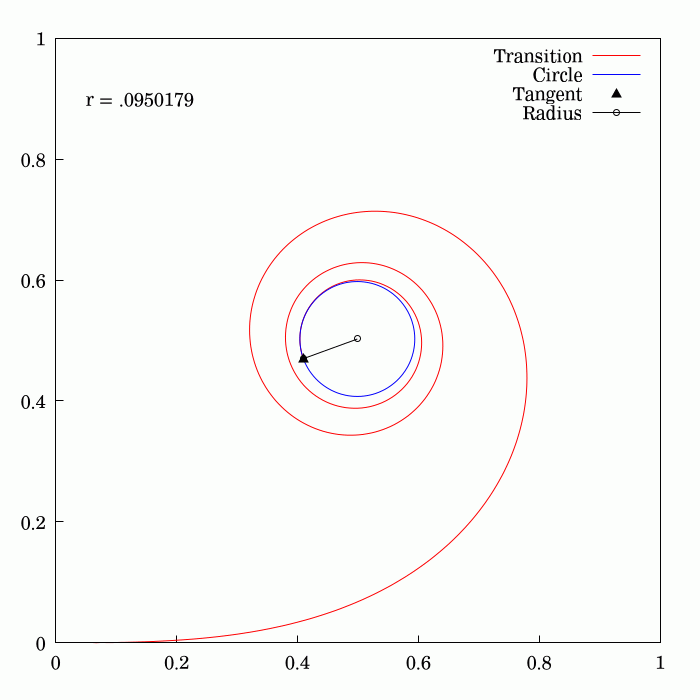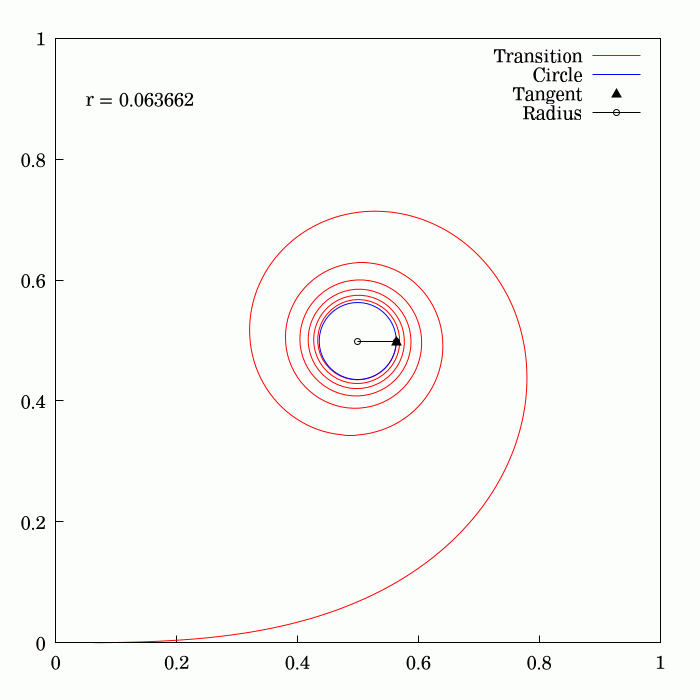
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The parametric curve is the Euler spiral or clothoid, a curve whose curvature varies linearly with arclength. The term Fresnel integral may also refer to the complex definite integral \int_^\infty e^ dx = \sqrte^ where is real and positive; this can be evaluated by closing a contour in the complex plane and applying Cauchy's integral theorem. Definition 250px, Fresnel integrals with arguments in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |