|
Extrapolation
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., extrapolation is a type of estimation, beyond the original observation range, of the value of a variable on the basis of its relationship with another variable. It is similar to interpolation, which produces estimates between known observations, but extrapolation is subject to greater uncertainty and a higher risk of producing meaningless results. Extrapolation may also mean extension of a wikt:method, method, assuming similar methods will be applicable. Extrapolation may also apply to human experience to project, extend, or expand known experience into an area not known or previously experienced. By doing so, one makes an assumption of the unknown [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Extrapolation Example
In mathematics, extrapolation is a type of estimation, beyond the original observation range, of the value of a variable on the basis of its relationship with another variable. It is similar to interpolation, which produces estimates between known observations, but extrapolation is subject to greater uncertainty and a higher risk of producing meaningless results. Extrapolation may also mean extension of a method, assuming similar methods will be applicable. Extrapolation may also apply to human experience to project, extend, or expand known experience into an area not known or previously experienced. By doing so, one makes an assumption of the unknownExtrapolation entry at Merriam–Webster (for example, a driver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
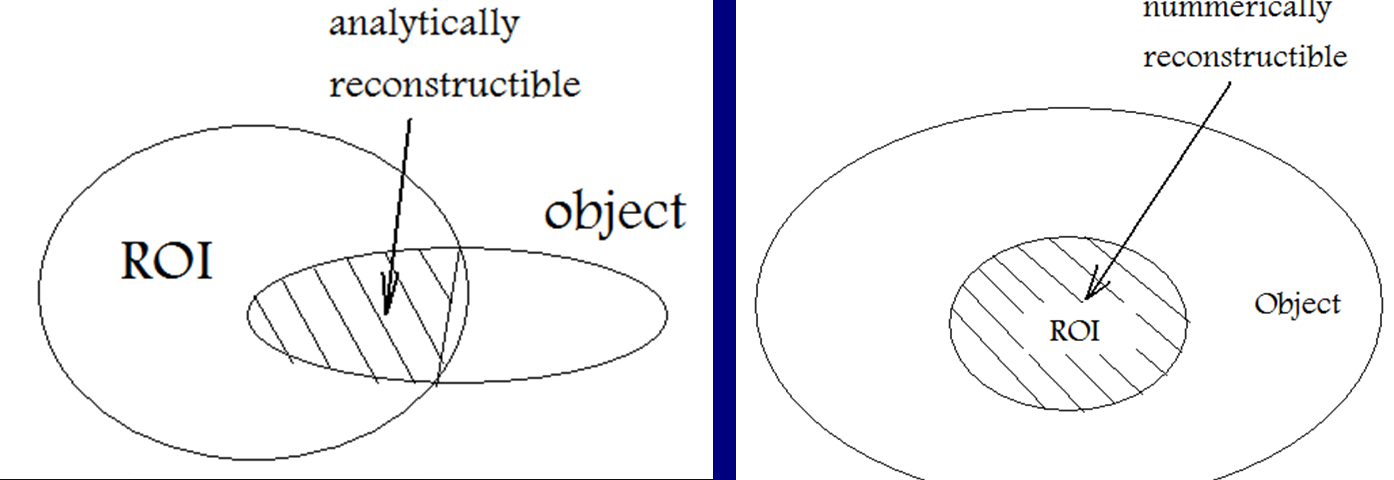 |
Interior Reconstruction
In iterative reconstruction in digital imaging, interior reconstruction (also known as limited field of view (LFV) reconstruction) is a technique to correct truncation artifacts caused by limiting image data to a small field of view. The reconstruction focuses on an area known as the region of interest (ROI). Although interior reconstruction can be applied to dental or cardiac X-ray computed tomography, CT images, the concept is not limited to CT. It is applied with one of several methods. Methods The purpose of each method is to solve for vector x in the following problem: : \begin f \\ g \end= \begin A & B \\ C & D \end \begin x \\ y \end. Let X be the region of interest (ROI) and Y be the region outside of X. Assume A, B, C, D are known matrices; x and y are unknown vectors of the original image, while f and g are vector measurements of the responses (f is known and g is unknown). x is inside region X, (x \in X) and y, in the region Y, (y \in Y), is outside region X. f is i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Linear Interpolation
In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points. Linear interpolation between two known points If the two known points are given by the coordinates (x_0,y_0) and the linear interpolant is the straight line between these points. For a value x in the interval the value y along the straight line is given from the equation of slopes \frac = \frac, which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with Solving this equation for y, which is the unknown value at x, gives \begin y &= y_0 + (x-x_0)\frac \\ &= \frac + \frac\\ &= \frac \\ &= \frac, \end which is the formula for linear interpolation in the interval Outside this interval, the formula is identical to linear extrapolation. This formula can also be understood as a weighted average. The weights are inversely related to the dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Interpolation
In the mathematics, mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing (finding) new data points based on the range of a discrete set of known data points. In engineering and science, one often has a number of data points, obtained by sampling (statistics), sampling or experimentation, which represent the values of a function for a limited number of values of the Dependent and independent variables, independent variable. It is often required to interpolate; that is, estimate the value of that function for an intermediate value of the independent variable. A closely related problem is the function approximation, approximation of a complicated function by a simple function. Suppose the formula for some given function is known, but too complicated to evaluate efficiently. A few data points from the original function can be interpolated to produce a simpler function which is still fairly close to the original. The resulting gai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component (topology), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Besides being a conic section, a hyperbola can arise as the locus (mathematics), locus of points whose difference of distances to two fixed focus (geometry), foci is constant, as a curve for each point of which the rays to two fix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
French Curve
A French curve is a template usually made from metal, wood or plastic Plastics are a wide range of synthetic polymers, synthetic or Semisynthesis, semisynthetic materials composed primarily of Polymer, polymers. Their defining characteristic, Plasticity (physics), plasticity, allows them to be Injection moulding ... composed of many different curved segments. It is used in manual Technical drawing, drafting and in fashion design to draw smooth curves of varying radii. The curve is placed on the drawing material, and a pencil, knife or other implement is traced around its curves to produce the desired result. They were invented by the German mathematician Ludwig Burmester and are also known as Burmester (curve) set. Clothing design French curves are used in fashion design and sewing alongside hip curves, straightedge, straight edges and square (tool), right-angle rulers. Pattern (sewing), Commercial clothing patterns can be personalized for fit by using French curves to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Smooth Function
In mathematical analysis, the smoothness of a function is a property measured by the number of continuous derivatives (''differentiability class)'' it has over its domain. A function of class C^k is a function of smoothness at least ; that is, a function of class C^k is a function that has a th derivative that is continuous in its domain. A function of class C^\infty or C^\infty-function (pronounced C-infinity function) is an infinitely differentiable function, that is, a function that has derivatives of all orders (this implies that all these derivatives are continuous). Generally, the term smooth function refers to a C^-function. However, it may also mean "sufficiently differentiable" for the problem under consideration. Differentiability classes Differentiability class is a classification of functions according to the properties of their derivatives. It is a measure of the highest order of derivative that exists and is continuous for a function. Consider an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Power Series
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a constant called the ''center'' of the series. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, the center ''c'' is equal to zero, for instance for Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. The partial sums of a power series are polynomials, the partial sums of the Taylor series of an analytic function are a sequence of converging polynomial approximations to the function at the center, and a converging power series can be seen as a kind of generalized polynom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Trigonometric Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Interval (mathematics)
In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |