|
Distance From A Point To A Plane
In Euclidean space, the distance from a point to a plane is the distance between a given point and its orthogonal projection on the plane, the perpendicular distance to the nearest point on the plane. It can be found starting with a change of variables that moves the origin to coincide with the given point then finding the point on the shifted plane ax + by + cz = d that is closest to the origin. The resulting point has Cartesian coordinates (x,y,z): :\displaystyle x = \frac , \quad \quad \displaystyle y = \frac , \quad \quad \displaystyle z = \frac . The distance between the origin and the point (x,y,z) is \sqrt. Converting general problem to distance-from-origin problem Suppose we wish to find the nearest point on a plane to the point (X_0, Y_0, Z_0), where the plane is given by aX + bY + cZ = D. We define x = X - X_0, y = Y - Y_0, z = Z - Z_0, and d = D - aX_0 - bY_0 - cZ_0, to obtain ax + by + cz = d as the plane expressed in terms of the transformed variables. Now the prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Hesse Normal Form
In analytic geometry, the Hesse normal form (named after Otto Hesse) is an equation used to describe a line in the Euclidean plane \mathbb^2, a plane in Euclidean space \mathbb^3, or a hyperplane in higher dimensions.John Vince: ''Geometry for Computer Graphics''. Springer, 2005, , pp. 42, 58, 135, 273 It is primarily used for calculating distances (see point-plane distance and point-line distance). It is written in vector notation as :\vec r \cdot \vec n_0 - d = 0.\, The dot \cdot indicates the dot product (or scalar product). Vector \vec r points from the origin of the coordinate system, ''O'', to any point ''P'' that lies precisely in plane or on line ''E''. The vector \vec n_0 represents the unit normal vector of plane or line ''E''. The distance d \ge 0 is the shortest distance from the origin ''O'' to the plane or line. Derivation/Calculation from the normal form Note: For simplicity, the following derivation discusses the 3D case. However, it is also applicable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Distance From A Point To A Line
The distance (or perpendicular distance) from a point to a line is the shortest Euclidean distance, distance from a fixed Point (geometry), point to any point on a fixed infinite Line (mathematics), line in Euclidean geometry. It is the length of the line segment which joins the point to the line and is perpendicular to the line. The formula for calculating it can be derived and expressed in several ways. Knowing the shortest distance from a point to a line can be useful in various situations—for example, finding the shortest distance to reach a road, quantifying the scatter on a graph, etc. In Deming regression, a type of linear curve fitting, if the dependent and independent variables have equal variance this results in orthogonal regression in which the degree of imperfection of the fit is measured for each data point as the perpendicular distance of the point from the regression line. Cartesian coordinates Line defined by an equation In the case of a line in the plane giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is one less than that of the ambient space. Two lower-dimensional examples of hyperplanes are one-dimensional lines in a plane and zero-dimensional points on a line. Most commonly, the ambient space is -dimensional Euclidean space, in which case the hyperplanes are the -dimensional "flats", each of which separates the space into two half spaces. A reflection across a hyperplane is a kind of motion ( geometric transformation preserving distance between points), and the group of all motions is generated by the reflections. A convex polytope is the intersection of half-spaces. In non-Euclidean geometry, the ambient space might be the -dimensional sphere or hyperbolic space, or more generally a pseudo-Riemannian space form, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
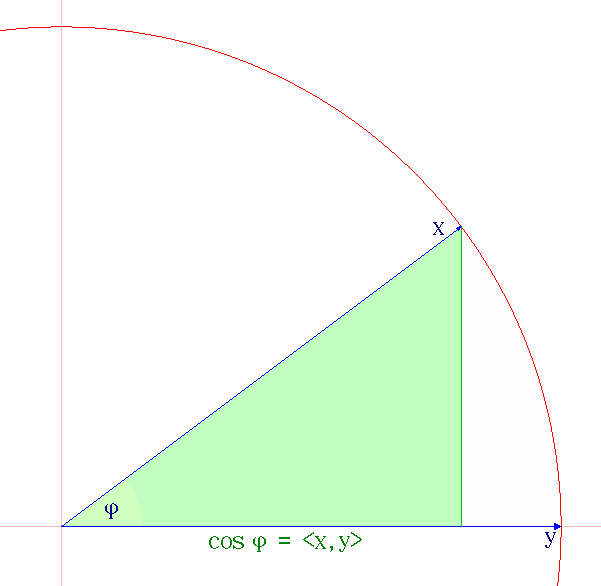 |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
 |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. The theorem can be written as an equation relating the lengths of the sides , and the hypotenuse , sometimes called the Pythagorean equation: :a^2 + b^2 = c^2 . The theorem is named for the Ancient Greece, Greek philosopher Pythagoras, born around 570 BC. The theorem has been Mathematical proof, proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both Geometry, geometric proofs and Algebra, algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Norm (mathematics)
In mathematics, a norm is a function (mathematics), function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the Origin (mathematics), origin: it Equivariant map, commutes with scaling, obeys a form of the triangle inequality, and zero is only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the #Euclidean norm, Euclidean norm, the #p-norm, 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meaning ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Orthogonal Projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P\colon V \to V such that P^2 = P. When V has an inner product and is complete, i.e. when V is a Hilbert space, the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. Not to be confused with scalar multiplication. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two Euclidean vector, vectors is widely used. It is often called the inner product (or rarely the projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see ''Inner product space'' for more). It should not be confused with the cross product. Algebraically, the dot product is the sum of the Product (mathematics), products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |