|
Distance-transitive Graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices and at any distance , and any other two vertices and at the same distance, there is an automorphism of the graph that carries to and to . Distance-transitive graphs were first defined in 1971 by Norman L. Biggs and D. H. Smith. A distance-transitive graph is interesting partly because it has a large automorphism group. Some interesting finite groups are the automorphism groups of distance-transitive graphs, especially of those whose diameter is 2. Examples Some first examples of families of distance-transitive graphs include: * The Johnson graphs. * The Grassmann graphs. * The Hamming Graphs (including Hypercube graphs). * The folded cube graphs. * The square rook's graphs. * The Livingstone graph. Classification of cubic distance-transitive graphs After introducing them in 1971, Biggs Biggs may refer to: Arts and entertainment * B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Livingstone Graph
In the mathematical field of graph theory, the Livingstone graph is a distance-transitive graph with 266 vertices and 1463 edges. Its intersection array In the mathematical field of graph theory, a distance-regular graph is a regular graph such that for any two Vertex (graph theory), vertices and , the number of vertices at distance (graph theory), distance from and at distance from depends ... is . It is the largest distance-transitive graph with degree 11. Algebraic properties The automorphism group of the Livingstone graph is the sporadic simple group J1, and the stabiliser of a point is PSL(2,11). As the stabiliser is maximal in J1, it acts primitively on the graph. As the Livingstone graph is distance-transitive, PSL(2,11) acts transitively on the set of 11 vertices adjacent to a reference vertex ''v'', and also on the set of 12 vertices at distance 4 from ''v''. The second action is equivalent to the standard action of PSL(2,11) on the projective line over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Dodecahedral Graph
A regular dodecahedron or pentagonal dodecahedronStrictly speaking, a pentagonal dodecahedron need not be composed of regular pentagons. The name "pentagonal dodecahedron" therefore covers a wider class of solids than just the Platonic solid, the regular dodecahedron. is a dodecahedron composed of regular pentagonal faces, three meeting at each vertex. It is an example of Platonic solids, described as cosmic stellation by Plato in his dialogues, and it was used as part of Solar System proposed by Johannes Kepler. However, the regular dodecahedron, including the other Platonic solids, has already been described by other philosophers since antiquity. The regular dodecahedron is a truncated trapezohedron because it is the result of truncating axial vertices of a pentagonal trapezohedron. It is also a Goldberg polyhedron because it is the initial polyhedron to construct new polyhedrons by the process of chamfering. It has a relation with other Platonic solids, one of them is the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Tutte–Coxeter Graph
In the mathematics, mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth (graph theory), girth 8, it is a cage (graph theory), cage and a Moore graph. It is bipartite graph, bipartite, and can be constructed as the Levi graph of the generalized quadrangle ''W''2 (known as the Cremona–Richmond configuration). The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers (Tutte 1958; Coxeter 1958a). All the cubic graph, cubic distance-regular graphs are known. The Tutte–Coxeter is one of the 13 such graphs. It has Crossing number (graph theory), crossing number 13, book thickness 3 and queue number 2.Wolz, Jessica; ''Engineering Linear Layouts with SAT.'' Master Thesis, Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Coxeter Graph
In the mathematics, mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 known cubic graph, cubic distance-regular graphs. It is named after Harold Scott MacDonald Coxeter. Properties The Coxeter graph has chromatic number 3, chromatic index 3, radius 4, diameter 4 and girth (graph theory), girth 7. It is also a 3-k-vertex-connected graph, vertex-connected graph and a 3-k-edge-connected graph, edge-connected graph. It has book thickness 3 and queue number 2. The Coxeter graph is hypohamiltonian graph, hypohamiltonian: it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It has Crossing number (graph theory), rectilinear crossing number 11, and is the smallest cubic graph with that crossing number . Construction The simplest construction of a Coxeter graph is from a Fano plane. Take the Combination, 7C3 = 35 possible 3-combinations on 7 obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pappus Graph
In the mathematical field of graph theory, the Pappus graph is a bipartite, 3- regular, undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic, distance-regular graphs are known; the Pappus graph is one of the 13 such graphs. The Pappus graph has rectilinear crossing number 5, and is the smallest cubic graph with that crossing number . It has girth 6, diameter 4, radius 4, chromatic number 2, chromatic index 3 and is both 3- vertex-connected and 3- edge-connected. It has book thickness 3 and queue number 2. The Pappus graph has a chromatic polynomial equal to: (x-1)x(x^ - 26x^ + 325x^ - 2600x^ + 14950x^ - 65762x^ + 229852x^ - 653966x^9 + 1537363x^8 - 3008720x^7 + 4904386x^6 - 6609926x^5 + 7238770x^4 - 6236975x^3 + 3989074x^2 - 1690406x + 356509) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Heawood Graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood. Combinatorial properties The graph is cubic, and all cycles in the graph have six or more edges. Every smaller cubic graph has shorter cycles, so this graph is the 6-cage, the smallest cubic graph of girth 6. It is a distance-transitive graph (see the Foster census) and therefore distance regular. Additions and Corrections to the book Distance-Regular Graphs (Brouwer, Cohen, Neumaier; Springer; 1989) There are 24 perfect matchings in the Heawood graph; for each matching, the set of edges not in the matching forms a Hamiltonian cycle. For instance, the figure shows the vertices of the graph placed on a cycle, with the internal diagonals of the cycle forming a matching. By subdividing the cycle edges into two matchings, we can partition the Heawood graph into three perfect matchings (that is, 3-color its edges) in eight different wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Cubical Graph
A cube or regular hexahedron is a three-dimensional solid object in geometry, which is bounded by six congruent square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with unit side length is the canonical unit of volume in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
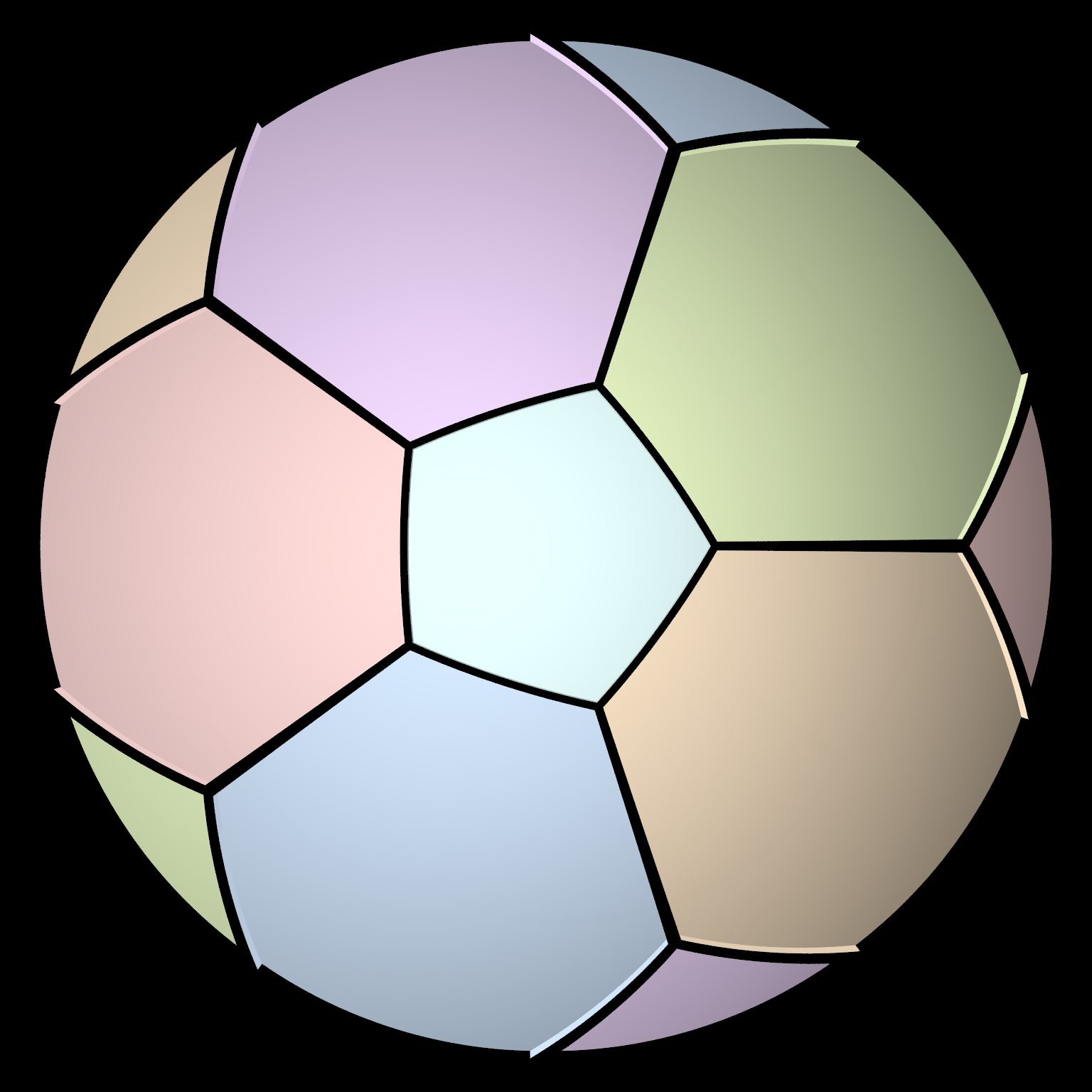 |
Petersen Graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three- edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by . Kempe observed that its vertices can represent the ten lines of the Desargues configuration, and its edges represent pairs of lines that do not meet at one of the ten points of the configuration. Donald Knuth states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general." The Petersen graph also makes an appearance in tropical geometry. The cone over the Petersen graph is naturally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Complete Bipartite Graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set..Electronic edition page 17. Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete bipartite graphs were already printed as early as 1669, in connection with an edition of the works of Ramon Llull edited by Athanasius Kircher. Llull himself had made similar drawings of complete graphs three centuries earlier.. Definition A complete bipartite graph is a graph whose vertices can be partitioned into two subsets and such that no edge has both endpoints in the same subset, and every possible edge that could connect vertices in different subsets is part of the graph. That is, it is a bipartite graph such that for every two vertices and, is an edge in . A complete bipartite graph w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Complete Graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction). Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete graphs, with their vertices placed on the points of a regular polygon, had already appeared in the 13th century, in the work of Ramon Llull. Such a drawing is sometimes referred to as a mystic rose. Properties The complete graph on vertices is denoted by . Some sources claim that the letter in this notation stands for the German word , but the German name for a complete graph, , does not contain the letter , and other sources state that the notation honors the contributions of Kazimierz Kuratowski to graph theory. has edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Tetrahedral Graph
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces. Re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |