|
Deterministic Context-free Language
In formal language theory, deterministic context-free languages (DCFL) are a proper subset of context-free languages. They are context-free languages that can be accepted by a deterministic pushdown automaton. DCFLs are always unambiguous, meaning that they admit an unambiguous grammar. There are non-deterministic unambiguous CFLs, so DCFLs form a proper subset of unambiguous CFLs. DCFLs are of great practical interest, as they can be parsed in linear time, and various restricted forms of DCFGs admit simple practical parsers. They are thus widely used throughout computer science. Description The notion of the DCFL is closely related to the deterministic pushdown automaton (DPDA). It is where the language power of pushdown automata is reduced to if we make them deterministic; the pushdown automata become unable to choose between different state-transition alternatives and as a consequence cannot recognize all context-free languages. Unambiguous grammars do not always generate a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language Theory
In logic, mathematics, computer science, and linguistics, a formal language is a set of string (computer science), strings whose symbols are taken from a set called "#Definition, alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called Formal language#Definition, ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Of A Formal Language
In mathematics and computer science, the right quotient (or simply quotient) of a language L_1 with respect to language L_2 is the language consisting of strings ''w'' such that ''wx'' is in L_1 for some string ''x'' in Formally: L_1 / L_2 = \ In other words, for all the strings in L_1 that have a suffix in L_2, the suffix is removed. Similarly, the left quotient of L_1 with respect to L_2 is the language consisting of strings ''w'' such that ''xw'' is in L_1 for some string ''x'' in L_2. Formally: L_2 \backslash L_1 = \ In other words, we take all the strings in L_1 that have a prefix in L_2, and remove this prefix. Note that the operands of \backslash are in reverse order: the first operand is L_2 and L_1 is second. Example Consider L_1 = \ and L_2 = \. Now, if we insert a divider into an element of L_1, the part on the right is in L_2 only if the divider is placed adjacent to a ''b'' (in which case ''i'' ≤ ''n'' and ''j'' = ''n'') or adjacent to a ''c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic Context-free Grammar
In formal grammar theory, the deterministic context-free grammars (DCFGs) are a proper subset of the context-free grammars. They are the subset of context-free grammars that can be derived from deterministic pushdown automata, and they generate the deterministic context-free languages. DCFGs are always unambiguous grammar, unambiguous, and are an important subclass of unambiguous CFGs; there are non-deterministic unambiguous CFGs, however. DCFGs are of great practical interest, as they can be parsed in linear time and in fact a parser can be automatically generated from the grammar by a parser generator. They are thus widely used throughout computer science. Various restricted forms of DCFGs can be parsed by simpler, less resource-intensive parsers, and thus are often used. These grammar classes are referred to by the type of parser that parses them, and important examples are LALR, SLR parser, SLR, and LL parser, LL. History In the 1960s, theoretical research in computer science o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deterministic Pushdown Automaton
In automata theory, a deterministic pushdown automaton (DPDA or DPA) is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages. Machine transitions are based on the current state and input symbol, and also the current topmost symbol of the stack. Symbols lower in the stack are not visible and have no immediate effect. Machine actions include pushing, popping, or replacing the stack top. A deterministic pushdown automaton has at most one legal transition for the same combination of input symbol, state, and top stack symbol. This is where it differs from the nondeterministic pushdown automaton. Formal definition A (not necessarily deterministic) PDA M can be defined as a 7-tuple: :M=(Q\,, \Sigma\,, \Gamma\,, q_0\,, Z_0\,, A\,, \delta\,) where *Q\, is a finite set of states *\Sigma\, is a finite set of input symbols *\Gamma\, is a finite set of stack symbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Context Free Language
In formal language theory, a context-free language (CFL), also called a Chomsky type-2 language, is a language generated by a context-free grammar (CFG). Context-free languages have many applications in programming languages, in particular, most arithmetic expressions are generated by context-free grammars. Background Context-free grammar Different context-free grammars can generate the same context-free language. Intrinsic properties of the language can be distinguished from extrinsic properties of a particular grammar by comparing multiple grammars that describe the language. Automata The set of all context-free languages is identical to the set of languages accepted by pushdown automata, which makes these languages amenable to parsing. Further, for a given CFG, there is a direct way to produce a pushdown automaton for the grammar (and thereby the corresponding language), though going the other way (producing a grammar given an automaton) is not as direct. Examples An exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Language
A computer language is a formal language used to communicate with a computer. Types of computer languages include: * Software construction#Construction languages, Construction language – all forms of communication by which a human can Computer programming, specify an executable problem solution to a computer ** Command language – a language used to control the tasks of the computer itself, such as starting programs ** Configuration file#Configuration languages, Configuration language – a language used to write configuration files ** Programming language – a formal language designed to communicate instructions to a machine, particularly a computer ***Scripting language – a type of programming language which typically is interpreted at runtime rather than being compiled ** Query language – a language used to make Information retrieval, queries in databases and information systems ** Transformation language – designed to transform some input te ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information And Control
''Information and Computation'' is a closed-access computer science journal published by Elsevier (formerly Academic Press). The journal was founded in 1957 under its former name ''Information and Control'' and given its current title in 1987. , the current editor-in-chief is David Peleg. The journal publishes 12 issues a year. History ''Information and Computation'' was founded as ''Information and Control'' in 1957 at the initiative of Leon Brillouin and under the editorship of Leon Brillouin, Colin Cherry and Peter Elias. Murray Eden joined as editor in 1962 and became sole editor-in-chief in 1967. He was succeeded by Albert R. Meyer in 1981, under whose editorship the journal was rebranded ''Information and Computation'' in 1987 in response to the shifted focus of the journal towards theory of computation and away from control theory. In 2020, Albert Mayer was succeeded by David Peleg as editor-in-chief of the journal. Indexing All articles from the ''Information and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LR Parser
In computer science, LR parsers are a type of bottom-up parsing, bottom-up parser that analyse deterministic context-free languages in linear time. There are several variants of LR parsers: SLR parsers, LALR parsers, canonical LR parser, canonical LR(1) parsers, canonical LR parser, minimal LR(1) parsers, and generalized LR parsers (GLR parsers). LR parsers can be generated by a parser generator from a formal grammar defining the syntax of the language to be parsed. They are widely used for the processing of computer languages. An LR parser (left-to-right, rightmost derivation in reverse) reads input text from left to right without backing up (this is true for most parsers), and produces a rightmost derivation in reverse: it does a bottom-up parsing, bottom-up parse – not a top-down parsing, top-down LL parse or ad-hoc parse. The name "LR" is often followed by a numeric qualifier, as in "LR(1)" or sometimes "LR(''k'')". To avoid backtracking or guessing, the LR parser is allowed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
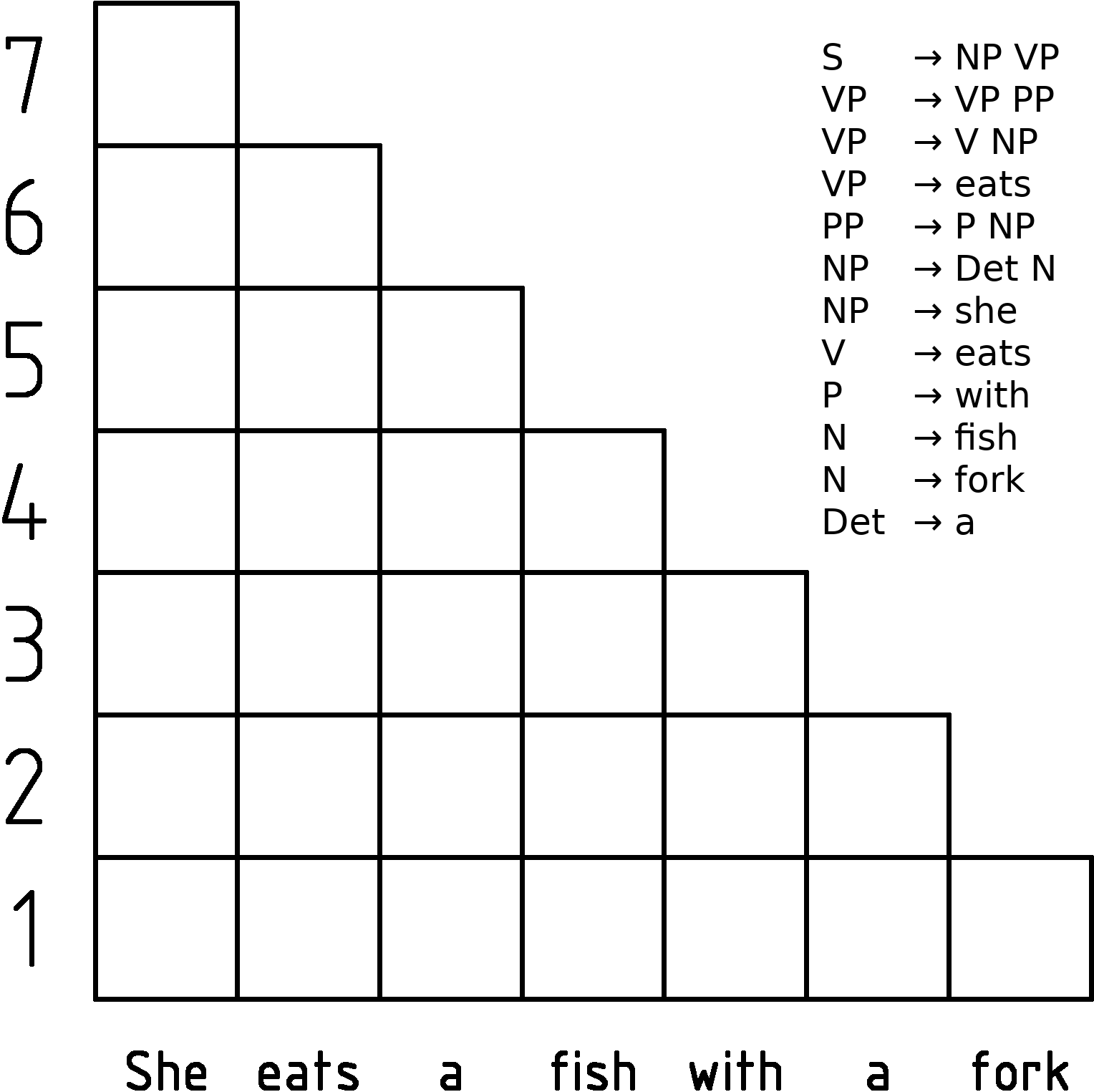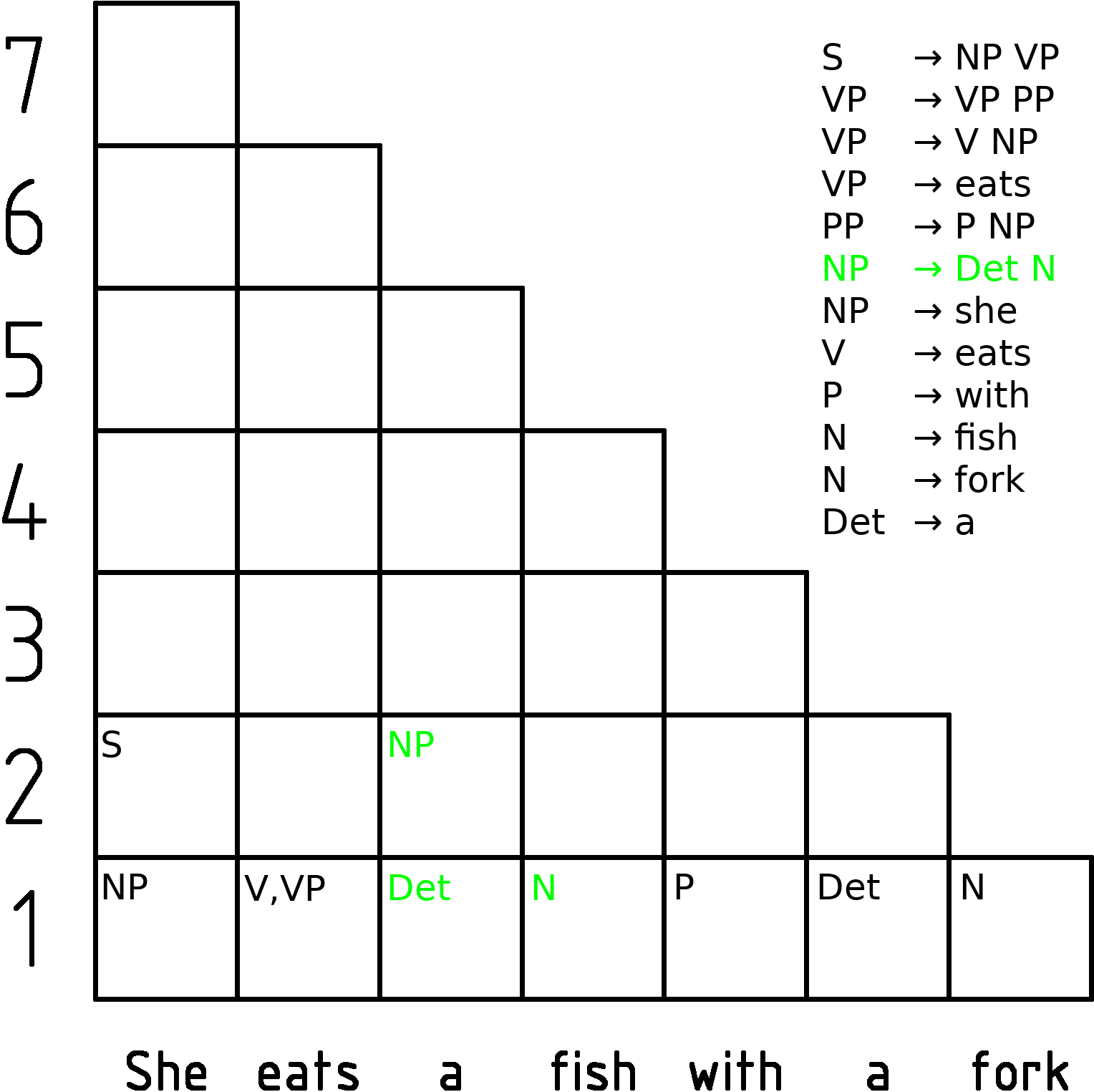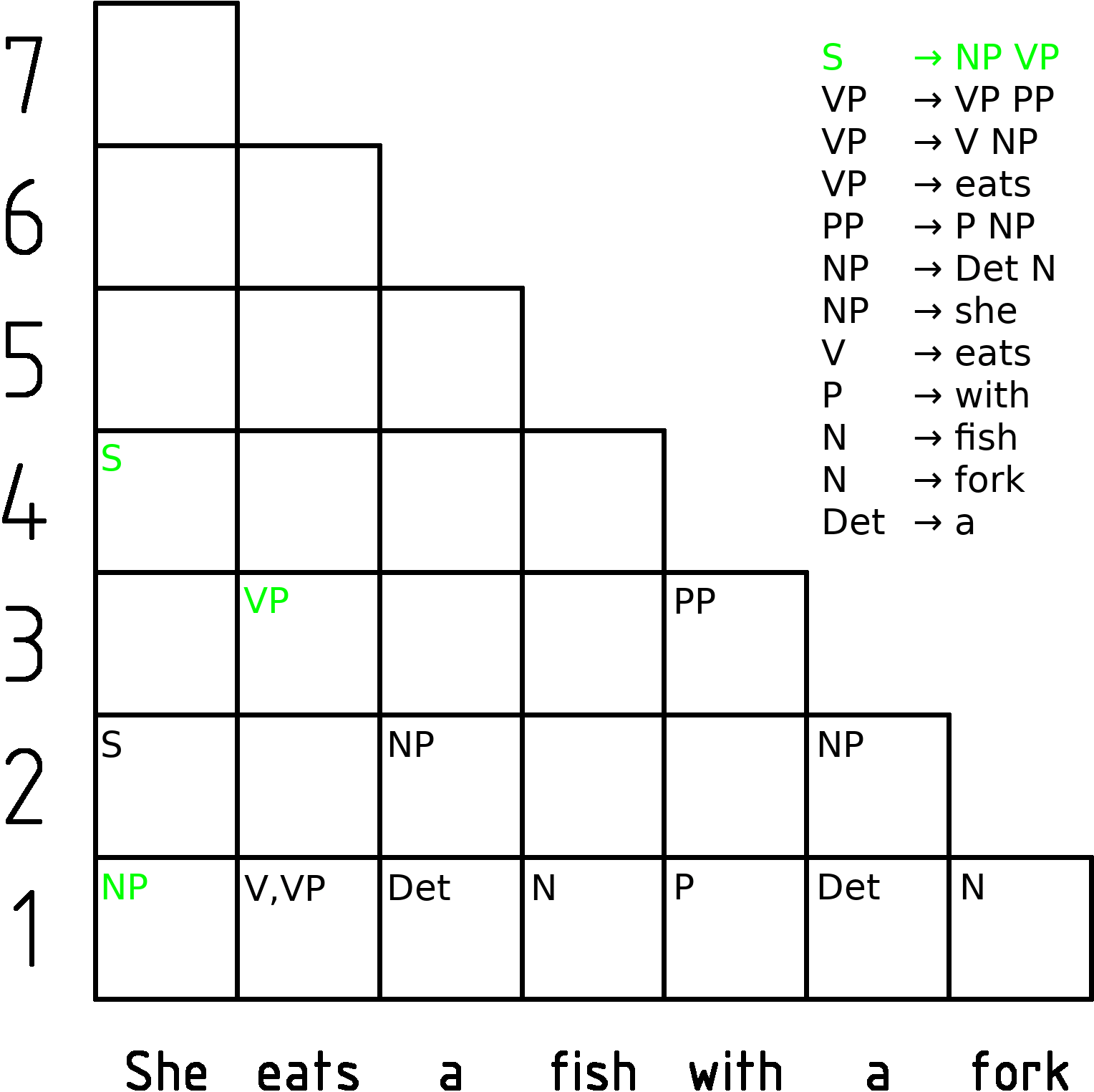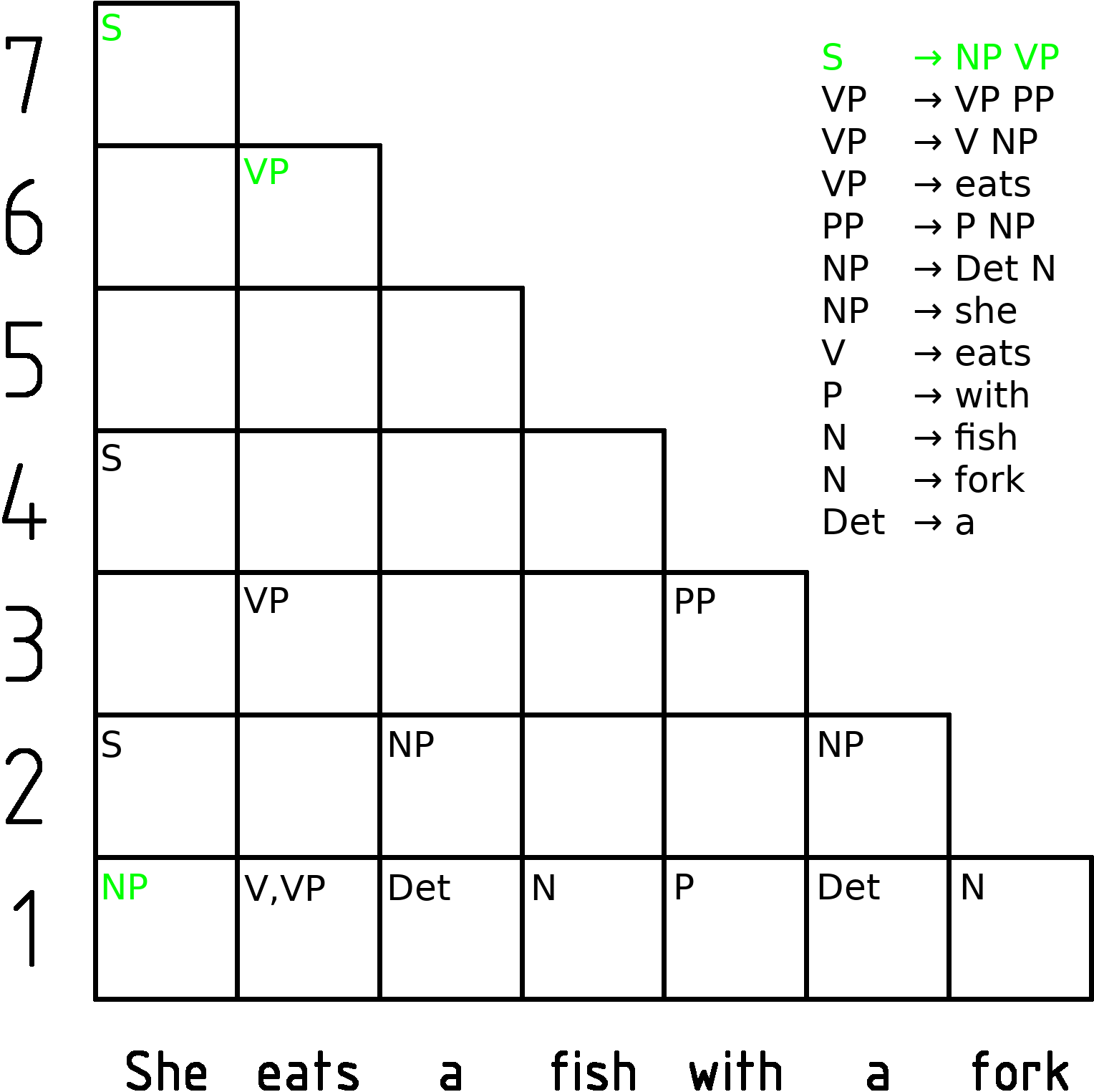
CYK Algorithm
In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961. The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming. The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language . The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big ''O'' notation, the worst case running time of CYK is \mathcal\left( n^3 \cdot \left, G \ \right), where n is the length of the parsed string and \left, G \ is the size of the CNF grammar G . This makes it one of the most efficient parsing algorithms in terms of worst-case asymptotic complexity, althoug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mirror Image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it results from specular reflection off from surfaces of lustrous materials, especially a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3D structures. In geometry and geometrical optics In two dimensions In geometry, the mirror image of an object or 2D geometric model, two-dimensional figure is the virtual image formed by reflection (mathematics), reflection in a plane mirror; it is of the same size as the original object, yet different, unless the object or figure has reflection symmetry (also known as a P-symmetry). Two-dimensional mirror images can be seen in the reflections of mirrors or other reflecting surfaces, or on a printed surface seen inside-out. If we first look at an obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene Star
In mathematical logic and theoretical computer science, the Kleene star (or Kleene operator or Kleene closure) is a unary operation on a Set (mathematics), set to generate a set of all finite-length strings that are composed of zero or more repetitions of members from . It was named after American mathematician Stephen Cole Kleene, who first introduced and widely used it to characterize Automata theory, automata for regular expressions. In mathematics, it is more commonly known as the free monoid construction. Definition Given a set V, define :V^=\ (the set consists only of the empty string), :V^=V, and define recursively the set :V^=\ for each i>0. V^i is called the i-th power of V, it is a shorthand for the Concatenation#Concatenation of sets of strings, concatenation of V by itself i times. That is, ''V^i'' can be understood to be the set of all strings that can be represented as the concatenation of i members from V. The definition of Kleene star on V is : V^*=\bigcup_V^i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concatenation
In formal language theory and computer programming, string concatenation is the operation of joining character strings end-to-end. For example, the concatenation of "snow" and "ball" is "snowball". In certain formalizations of concatenation theory, also called string theory, string concatenation is a primitive notion. Syntax In many programming languages, string concatenation is a binary infix operator, and in some it is written without an operator. This is implemented in different ways: * Overloading the plus sign + Example from C#: "Hello, " + "World" has the value "Hello, World". * Dedicated operator, such as . in PHP, & in Visual Basic, and , , in SQL. This has the advantage over reusing + that it allows implicit type conversion to string. * string literal concatenation, which means that adjacent strings are concatenated without any operator. Example from C: "Hello, " "World" has the value "Hello, World". In many scientific publications or standards the con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |