|
De Quinque Corporibus Regularibus
''De quinque corporibus regularibus'' (sometimes called ''Libellus de quinque corporibus regularibus'') is a book on the geometry of polyhedra written in the 1480s or early 1490s by Italian painter and mathematician Piero della Francesca. It is a manuscript, in the Latin language; its title means '' he little bookon the five regular solids''. It is one of three books known to have been written by della Francesca. Along with the Platonic solids, ''De quinque corporibus regularibus'' includes descriptions of five of the thirteen Archimedean solids, and of several other irregular polyhedra coming from architectural applications. It was the first of what would become many books connecting mathematics to art through the construction and perspective drawing of polyhedra, including Luca Pacioli's 1509 '' Divina proportione'' (which incorporated without credit an Italian translation of della Francesca's work). Lost for many years, ''De quinque corporibus regularibus'' was rediscovered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piero Della Francesca - Libellus De Quinque Corporibus Regularibus - P1b
Piero is an Italian given name. Notable people with the name include: *Piero Angela (1928–2022), Italian television host * Piero Barucci (born 1933), Italian academic and politician *Piero Cassano (born 1948), Italian keyboardist, singer and composer, a founding member of the Genoan band Matia Bazar *Piero del Pollaiuolo (c. 1443–1496), Italian painter *Piero della Francesca (c1415–1492), Italian artist of the Early Renaissance * Piero De Benedictis (born 1945), Italian-born Argentine and Colombian folk singer * Piero Ciampi (1934–1980), Italian singer *Piero di Cosimo (1462-1522), also known as Piero di Lorenzo, Italian Renaissance painter *Piero di Cosimo de' Medici (1416–1469), ''de facto'' ruler of Florence from 1464 to 1469 *Piero Ferrari (born 1945), Italian businessman *Piero Focaccia (born 1944), Italian pop singer * Piero Fornasetti (1913–1988), Italian painter * Piero Gardoni (1934–1994), Italian professional footballer * Piero Golia (born 1974), Italian conce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
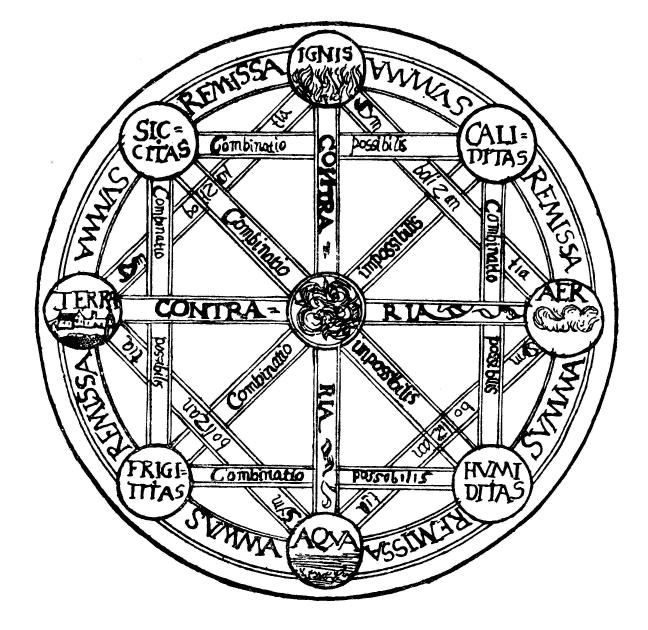
Classical Elements
The classical elements typically refer to earth, water, air, fire, and (later) aether which were proposed to explain the nature and complexity of all matter in terms of simpler substances. Ancient cultures in Greece, Angola, Tibet, India, and Mali had similar lists which sometimes referred, in local languages, to "air" as "wind", and to "aether" as "space". These different cultures and even individual philosophers had widely varying explanations concerning their attributes and how they related to observable phenomena as well as cosmology. Sometimes these theories overlapped with mythology and were personified in deities. Some of these interpretations included atomism (the idea of very small, indivisible portions of matter), but other interpretations considered the elements to be divisible into infinitely small pieces without changing their nature. While the classification of the material world in ancient India, Hellenistic Egypt, and ancient Greece into air, earth, fir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference. Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter; if the length of the string was exact, it would equal the perimeter. Formulas The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with \int_0^L \mathrms, where L is the length of the path and ds is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Initial
In a written or published work, an initial is a letter at the beginning of a word, a chapter (books), chapter, or a paragraph that is larger than the rest of the text. The word is ultimately derived from the Latin ''initiālis'', which means ''of the beginning''. An initial is often several lines in height, and, in older books or manuscripts, may take the form of an inhabited or historiated initial. There are certain important initials, such as the Beatus initial, or B, of ''Beatus vir...'' at the opening of Psalm 1 at the start of a vulgate Latin. These specific initials in an illuminated manuscript were also called initia (grammatical number, singular: initium). History The classical tradition was slow to use capital letters for initials at all; in surviving Roman texts it often is difficult even to separate the words as spacing was not used either. In late antiquity (–6th century) both came into common use in Italy, the initials usually were set in the left margin (as in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sansepolcro
Sansepolcro, formerly Borgo Santo Sepolcro, is a town and ''comune'' founded in the 11th century, located in the Italian Province of Arezzo in the eastern part of the region of Tuscany. Situated on the upper reaches of the Tiber river, the town is the birthplace of the painters Piero della Francesca, Raffaellino del Colle (a pupil of Raphael), Matteo di Giovanni, Santi di Tito, and Angiolo Tricca. It was also the birthplace of the Italian mathematician Luca Pacioli, and of Matteo Cioni, who translated Piero della Francesca's treatise about perspective in painting ('' De prospectiva pingendi'') into Latin. Today, the economy of the town is based on agriculture, industrial manufacturing, food processing and pharmaceuticals. It is the home of Buitoni pasta, founded by Giulia Buitoni in 1827. History According to tradition the founding of the town came about through two 9th-century pilgrims to the Holy Land, Arcanus and Giles. They returned to the region and built a chapel de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liber Abaci
The or (Latin for "The Book of Calculation") was a 1202 Latin work on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci. It is primarily famous for introducing both base-10 positional notation and the symbols known as Arabic numerals in Europe. Premise was among the first Western books to describe the Hindu–Arabic numeral system and to use symbols resembling modern "Arabic numerals". By addressing the applications of both commercial tradesmen and mathematicians, it promoted the superiority of the system and the use of these glyphs. Although the book's title is sometimes translated as "The Book of the Abacus", notes that it is an error to read this as referring to the abacus as a calculating device. Rather, the word "abacus" was used at the time to refer to calculation in any form; the spelling "abbacus" with two "b"s was, and still is in Italy, used to refer to calculation using Hindu-Arabic numerals, which can avoid confusion. The book describes methods o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages". The name he is commonly called, ''Fibonacci'', is first found in a modern source in a 1838 text by the Franco-Italian mathematician Guglielmo Libri Carucci dalla Sommaja, Guglielmo Libri and is short for ('son of Bonacci'). However, even as early as 1506, Perizolo, a notary of the Holy Roman Empire, mentions him as "Lionardo Fibonacci". Fibonacci popularized the Hindu–Arabic numeral system, Indo–Arabic numeral system in the Western world primarily through his composition in 1202 of (''Book of Calculation'') and also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in . Biography Fibonacci was born around 1170 to Guglielmo, an Italian merchant and customs official who directed a trading post in Béjaïa, Bugia, modern-day Béjaïa, Algeria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perspective Drawing
Linear or point-projection perspective () is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of an image as it is seen by the eye. Perspective drawing is useful for representing a three-dimensional scene in a two-dimensional medium, like paper. It is based on the optical fact that for a person an object looks N times (linearly) smaller if it has been moved N times further from the eye than the original distance was. The most characteristic features of linear perspective are that objects appear smaller as their distance from the observer increases, and that they are subject to , meaning that an object's dimensions parallel to the line of sight appear shorter than its dimensions perpendicular to the line of sight. All objects will recede to points in the distance, usually along the horizon line, but also above and below the horizon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cloister Vault
In architecture, a cloister vault (also called a pavilion vault) is a Vault (architecture), vault with four convex surfaces (patches of cylinder (geometry), cylinders) meeting at a point above the center of the vault. It can be thought of as formed by two barrel vaults that cross at right angles to each other: the open space within the vault is the Intersection (set theory), intersection of the space within the two barrel vaults, and the solid material that surrounds the vault is the Union (set theory), union of the solid material surrounding the two barrel vaults. In this way it differs from a groin vault, which is also formed from two barrel vaults but in the opposite way: in a groin vault, the space is the union of the spaces of two barrel vaults, and the solid material is the intersection. A cloister vault is a square domical vault, a kind of vault with a polygonal base. Domical vaults can have other polygons as cross-sections (especially octagons) rather than being limited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pappus Of Alexandria
Pappus of Alexandria (; ; AD) was a Greek mathematics, Greek mathematician of late antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem in projective geometry. Almost nothing is known about his life except for what can be found in his own writings, many of which are lost. Pappus apparently lived in Alexandria, where he worked as a Mathematics education, mathematics teacher to higher level students, one of whom was named Hermodorus.Pierre Dedron, J. Itard (1959) ''Mathematics And Mathematicians'', Vol. 1, p. 149 (trans. Judith V. Field) (Transworld Student Library, 1974) The ''Collection'', his best-known work, is a compendium of mathematics in eight volumes, the bulk of which survives. It covers a wide range of topics that were part of the ancient mathematics curriculum, including geometry, astronomy, and mechanics. Pappus was active in a period generally considered one of stagnation in mathematical studies, where, to s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |